
大阪大学ベクトル問題
お世話になります。岡山で理系に強い予備校・岡山進学研究塾です。今回は、2023年の大阪大学ベクトル問題(文理共通)の解説です。文系はこの大問を完投すればほぼ合格は間違いなし(余程英国でコケたら話は別ですが)、理系は完答必須、と言ったところでしょう。京大・阪大の平面幾何特有のポイントも併せて示唆しようかと思います。
岡山進学研究塾HP https://okashinken.org/
E-mail study_support@okashinken.com
Tel 086-207-2450
阪大数字
文理問わずベクトル問題でよく使う手があります。今回、(2)で使いますのでご注目を。では、初めていきます。
問題文から情報整理

解く前の準備、情報整理からです。
2・ベクトルOA +ベクトルOBの原点からの長さが2・ベクトルOB+ベクトルOAの長さに等しく、両者の値が共に1。
→式が3つ(正味、2つで構いませんが)作れます。
もう一つは内積の式。両者を展開して出てくる項は
・ベクトルOAとベクトルOBの長さ、あと内積です。これらを求めて(1)の式へ代入すれば、おのずと答えが出る。
単なる計算問題ですよ。
幾何的考察を要するか否か、前回の一橋大のベクトル問題で述べた通りです。
(一橋大のベクトル問題は以下を参照のこと)


続きを計算します。

計算ミスだけ気を付けていればなんてことありません。重要なのはここからです。
平面を自分で定義する
これが京大・阪大数学の常套手段です。(1)の結果から二つのベクトルは直交することが分かる
直交→片方をx軸、もう片方をy軸に添わせる。出題者からは直交以外何も制約がないため、支障はない。
要は、解きやすいように二つのベクトルの関係性だけを保持して平面自体は自分で定義すれば良いんですよ。

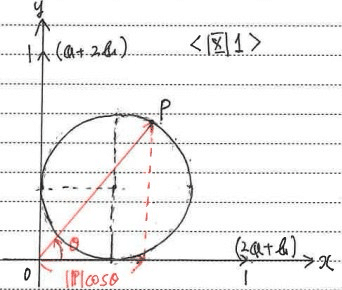
どうです?この平面図を見ながら解くのは、かなりラクではありませんか?
(2)の一つ目の条件式から、点Pは図1の円内部と分かります。また、ベクトルOA +ベクトルOBの位置は絶対値2乗と(1)の結果から値は容易に算出できます。

途中の重要ポイントは以下に記す。


図1のOPの長さの余弦も図示していれば直ぐに分かります。

赤字で書いた部分が非常に重要です。どのように正確な図へ近づくか、のプロセスなんですよ。
続きはこうなります。


最終的な条件は全て図示したものに沿って幾何的に導かれていきます。


このタイプの問題は京大でもよく出題されます。中には解法パターンとして網羅されている方もおられるかも知れませんが、文理問わず自分で平面定義して解くのは常套手段として解釈して問題ありません。
解説を以下に纏めます。


まとめ
阪大の数学は式処理で済む問題も割と多く感じますが、中には幾何的考察抜きには解けないものも存在します。今回は問題を解くために必要な要素を見抜く一環としてレクチャーしました。
岡山進学研究塾では2023年度冬季講習を実施しています。受講者には好評でより高いレベルを短期間で提供できるよう、指導方針にもこだわりを持って取り組んでいます。お問合せは校舎までどうぞ。

校舎公式LINEはこちらからどうぞ。

公式LINE登録後はひと言チャットの方へメッセージを頂ければ、こちらからご返信致します。
