
宇宙はどうして美しいのか?(その1)

1.宇宙は美しい
書店や図書館には、まさにあふれるほどの、天体写真集が並んでいる。そこに掲載された写真は、カラー作品もモノクロ作品も、本当に美しい。


私自身、中学生の時に天文雑誌と出会い、「なんて美しい世界があったんだ」と思って、学校の図書室や町の図書館にある天体写真集を眺め、そこからやがて星・宇宙の世界に入っていった1人である。
やがて自身で星座写真や天体写真を撮るようになったのも、自然な流れ。フィルム時代もそれなりに楽しんだが、デジタルカメラ時代になっても、その楽しさは変わらない。ただ、デジタル時代になると、画像処理技術が進んで、アマチュアでも天文台の大望遠鏡に匹敵するような美しい天体画像を作っては公開できるようになると、自分で撮るより、人が撮って作成した美しい画像を眺めるだけで良いかな、などと思ってしまう。
ところで、アマチュアのみならず、天文台が公開する天体の画像は本当に美しい。もっとも天文学者がその画像を使って研究するのではなく、それはあくまで一般に公開するために作成した画像であったことを知るようになったのは、天体写真を趣味にするようになってしばらくしてから。つまりは、天文台の広報部門が美しい画像を”作って“公開していたワケではあるが、それでも天文学者さんたちがソレを”美しい“と感じたから、それを伝えるために画像を”作って“いるのだという。
そんなとき、フト思った。どうして人はこれらの天体を“美しい”と感じるのだろう? 人はどういうモノを“美しい”と感じるのだろう?
そんな疑問を抱いて幾星霜、興味深い本が出版された。書名はまさに『宇宙はなぜ美しいか』! サブタイトルは『~究極の「宇宙の法則」を目指して~』 「Beyond講座」で、この本の内容を紹介する講義をした。

この本では、物理学者はどういうモノを“美しい”と感じるかについて解説したもの。学者の目から見ても、この世界が以下に美しいかを昔から多くの人が語っている。映画『コンタクト』でワームホールで銀河系の外に導かれたエリーが、銀河系の美しさを表現する言葉を持っていなかったため「詩人が来るべきだった」と語ったのは興味深い。
2.学者はどういうモノを美しいと思うか ~簡潔なモノ~
学者が“美しい”と感じるモノを、いくつかに分類することができる。一つは“簡潔なモノ”。

物理学で現象を数式で論じるようになったのはいつからかは知らないが、その数式が“簡潔”であるほどに、“美しい”と感じるほどに、学者はその数式が正しいと考えるという。そして実際、複雑な数式より簡潔な数式の方が正しいという。
「世界でもっとも美しい10の物理方程式」というものがある。「ピタゴラスの定理」「ニュートンの運動の第二法則」「アインシュタインの質量とエネルギーの等価性を表す式」などはよく知られているだろう。

この他に、物理学で「オッカムのカミソリ」というものもある。14世紀の哲学者・神学者オッカムが多用したことで知られているもので、「ある事柄を説明するのであれば、仮説の数は少ない方が良い」「説明する理論・法則は、比較的に単純な方がよい」というものもある。これも“簡潔”なものが“美しく”、また正しいという一例であろう。
3.学者はどういうモノを美しいと思うか ~対称性~
学者に限らず一般の人も、「対称性(シンメトリー)」なものを“美しい”と感じる。左右または上下が対象なものを物理学や数学では「対称性:1つ」、左右および上下が対象なものを「対称性:2つ」と数えるのだそうだ。
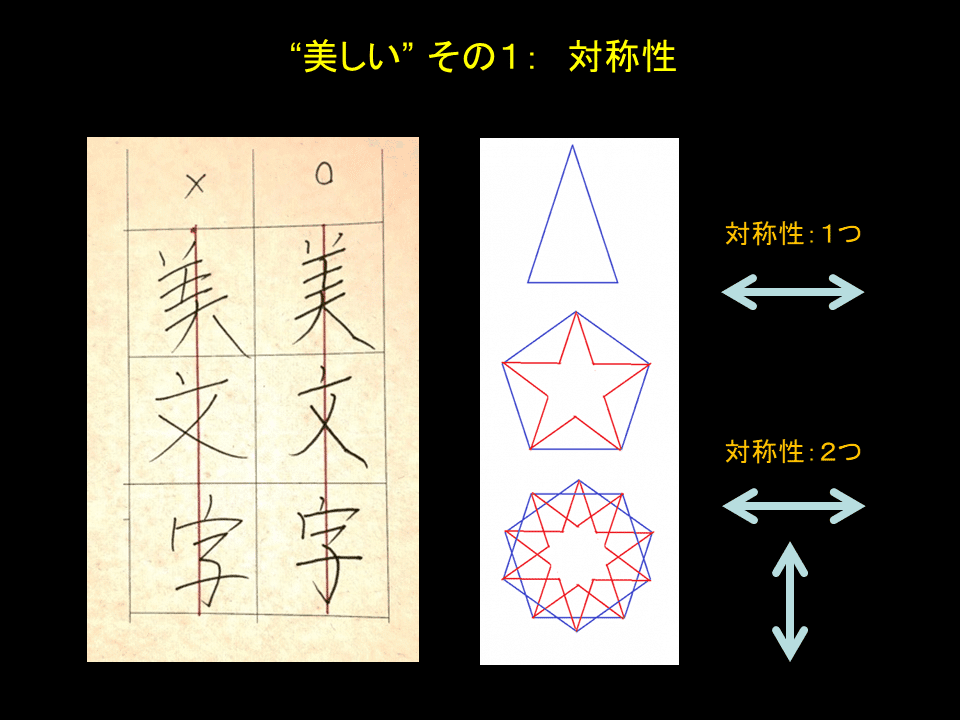
古代ギリシャ文化をベースに持つ欧米人は特に、この“対称性”を持つモノを“美しい”と感じるようだ。建築物でも左右が対称であれば“美しい”とし、さらにその姿が水面に映るとさらに“美しい”とする。

天体画像でも、「地球の出」や惑星の球形は“美しい”。一方、小惑星はでこぼこしていて、“おもしろい”とは言うが、“美しい”とは言わない。銀河でも、渦巻き銀河のように対称性のあるものは“美しい”とし、不規則銀河は“キレイ”とは言っても、“美しい”とは言わない。


4.学者はどういうモノを美しいと思うか ~シンプルなモノ~
「2」で述べた「簡潔なモノ」と同じだが、天文学や物理学の歴史では“シンプル”なものを“美しく”、また“正しい”としてきた。
古代ギリシャ時代以降ずっと、地球(大地)を回る惑星(日月を含む)の公転軌道は、最も美しい図形である円軌道とされてきた。また月を含む天体は最も美しい立体である完全な球形をしているとも考えられてきた。

16世紀にコペルニクスが、それまでの地球中心説から太陽中心説を唱えても、惑星の軌道は円軌道のままだった。ティコ・ブラーエが、惑星が太陽を中心に廻ることを了解しても、軌道はやはり円軌道だった。ただ、ティコの惑星軌道図は“美しい”とは言えないだろう。

ティコの観測データを引き継いだケプラーは、火星の軌道を研究した際、火星の位置が円軌道でのものからほんの少しズレが生じていることを無視できず、それを説明するために、火星の軌道は楕円であるとした(ケプラーの惑星軌道の第1法則)。惑星の軌道の“美しさ”を求め続けたケプラーが、惑星の軌道が真円ではなく楕円だと判じた時の苦悩は想像に難い。ただ、楕円軌道としながらも、楕円には焦点が2つあり、惑星軌道は太陽を焦点の1つに置き、太陽に近いところでは速く動き、遠いところでは遅く動いて、同じ時間で移動する円弧と太陽を結んでできる扇型の面積が一定である(面積速度一定の法則、ケプラーの第2法則)という “美しい” 法則は、ケプラーの苦悩を和らげはしただろう。

また、円や楕円は「円錐曲線」の一つで、真円は楕円の傾きがゼロである特殊な図形(軌道)であることも、ケプラーの苦悩を和らげたことと思う。そしてこの説明もまた“美しい”。
さらにケプラーは、惑星の軌道の大きさと公転周期の関係にも美を発見した。公転周期の2乗が軌道の大きさの3乗と等しいのだ。この、2と3というシンプルな数で等式が作られるという発見は、ケプラーに極上の感動を与えたことだろう。ケプラーはこの法則に「調和の法則」と名付けた(ケプラーの第3法則)。

このようにケプラーの惑星軌道の法則は、ケプラーが求め続けた惑星軌道の“美しさ”で満ちている。
