【保存版】多項式補間の一つのラグランジュ補間について学んでみよう！

０　はじめに

私は、高校時代、数学が好きでした（数学III・Cまでやりました）が、大学は文系に進みました。

最近になり、約15年ぶりに数学を学び直し始めました。

間違いのないように、一つ一つ理解しながら進んでいるつもりではありますが、何か気になるところがありましたら、優しく教えていただくと嬉しいです。

一つ一つ丁寧に学んでいきたいと思っています。

１　多項式補間とは

まずはWikipediaからの引用です。

多項式補間（たこうしきほかん、英: polynomial interpolation）は、数値解析において、与えられたデータ群を多項式で内挿（補間）することである。言い換えれば、標本調査などで得たデータ群について、それらを正確に通る多項式を見つけることである。

私は、「（N + 1）個の点があったとき、その点を通る、唯一のN次関数を見つけること」だと理解しました。

例えば、

２つの点があった時、その点を通る、唯一の１次関数を見つけたり、

３つの点があった時、その点を通る、唯一の２次関数を見つけるということです。

２　複数の点を通る関数は一つだけ？

では、仮に、下のように、３つの点を通る、２次関数について考えてみましょう。

フリーハンドですし、実際とは異なっていると思いますが、イメージとして、下のような唯一の２次関数ができます。

では、次に、２つの点を通る、１次関数を考えてみましょう。

こちらも、下のような唯一の１次関数が決まります。

では、２つの点を通る、２次関数はどうでしょう？

その場合、下のように、無数に存在します。

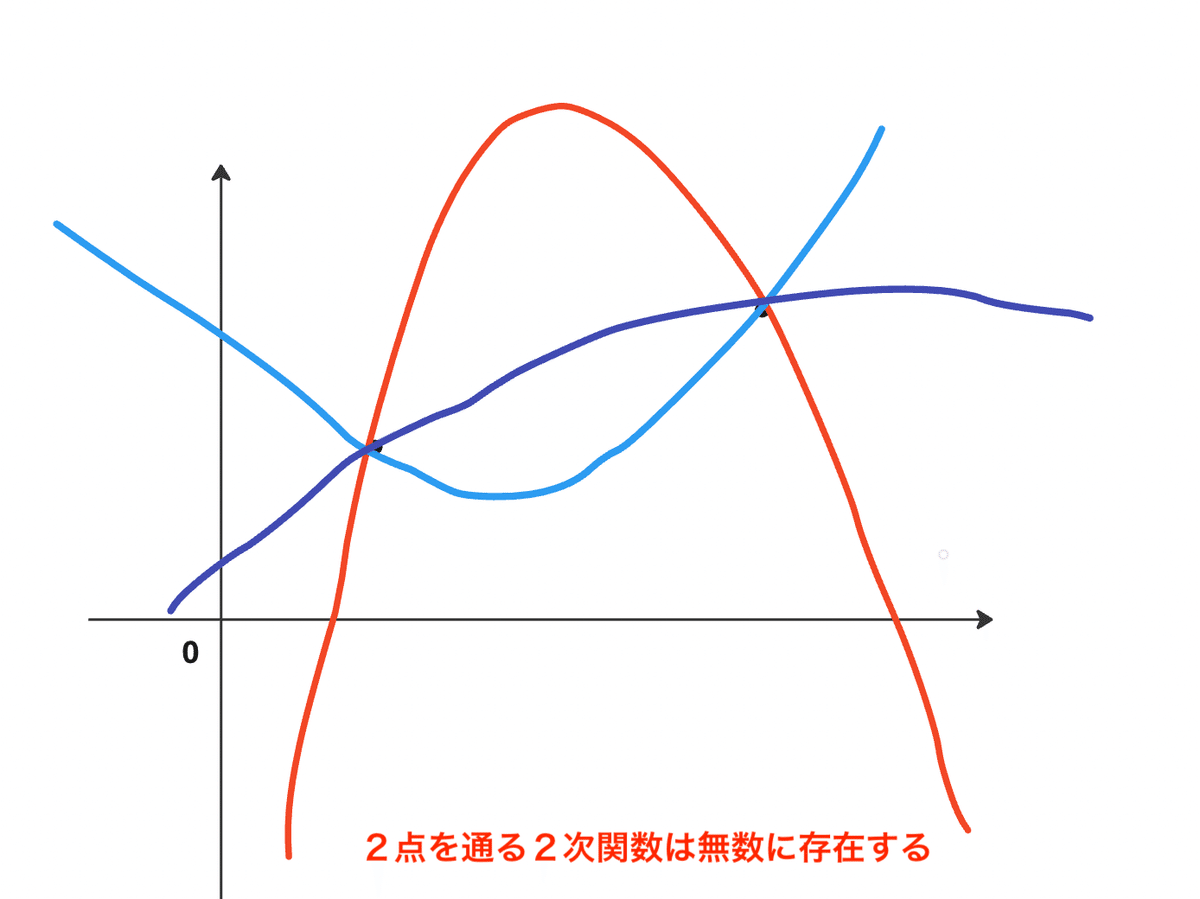
そのため、（N + 1） 個の点を通る、N次関数は一意に決まるということを押さえると良いと思いました。

３　（N + 1） 個の点を通る、N次関数は必ず存在する？

これは、後ほど、「ラグランジュ補間」の例で見てみましょう。

Nの数に関わりなく、求めることができることが確認できると思います。

４　ラグランジュ補間について

では、多項式補間の一つである、ラグランジュ補間の求め方について学んでみましょう。

１　前提について

まずは、下のような問題を考えてみましょう。

これは、下のように作ることができます。

実際に代入すると、このように、うまく求まることがわかります。

別の例でも試してみましょう。

やはり、同様に、求めることができました。

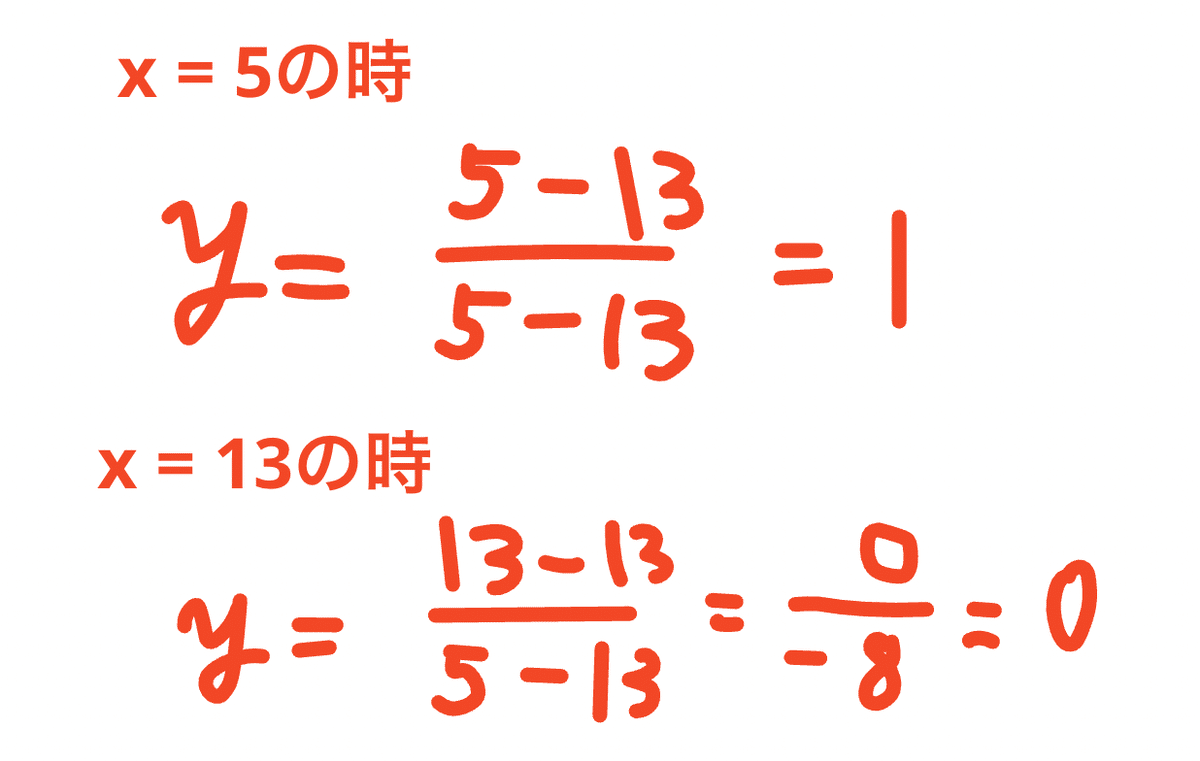
２　任意の２点を通る１次関数を求める

では、下のケースを考えてみましょう。

ラグランジュ補間を理解するために、まずは、Y座標を共に１として考えます。

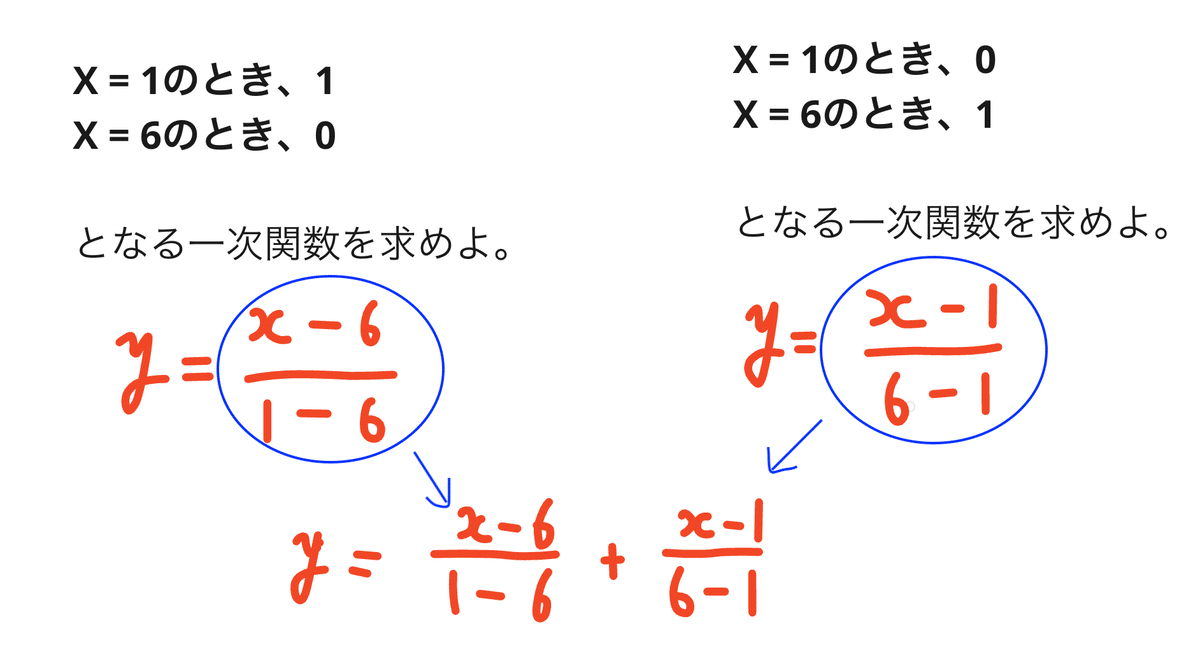
ところで、第１節で、下のような１次関数を求める方法を学びました。

同様に、こちらも求められますね。（上から、０と１を逆にしています。）

これをくっつけると、下のようになります。

実は、これが(1, 1), (6, 1)を通る１次関数になっています。

なぜかも考えてみましょう。

下のように、どちらかが１になる時、もう一方が0となり、お互い無視することができるからです。

つまり、(1, 1), (6, 1)を通る１次関数は下のようになりました。

（整理すれば、綺麗になりますが、ここでは特に整理せず、このまま行きます。）

では、実際のY座標も含めて考えてみましょう。

下のように、x = 1の時、左側が１になったので、３にするには３倍すれば良いです。

x = 1の時、右側は0なので、考える必要がありません。

もう一方も同様です。

下のように、x = 6の時、右側が１になったので、２にするには２倍すれば良いです。

x = 6の時、左側は0なので、考える必要がありません。

これで、(1, 1), (6, 1)を通る１次関数を求めることができました。

３　個数を増やすとどうなるか

例えば、点を一つ増やし、２次関数を求めてみます。

結果は、下のようになります。

このように、個数を増やしたとしても、同様のやり方で求めることができることがわかりました。

今回は以上です。