
これからの「クロック」の話をしよう
↑ いいねお願いします!
みなさんこんにちは。いかのおすしです。
クロックやっていますでしょうか?最近は国内外問わず、クロックが盛況ですね。世界記録は単発2.40、平均2.52と訳の分からない世界へ突入してきました。個人的には、単発sub2はいつか誰かが出してくれるのではと思っています。
日本でも最近クロックが人気ですね。大会初心者ウェルカムのチャレンジ大会と銘打った大会が、クロック2ラウンドだけとかいう正気では考えられない種目構成であったり、その大会の決勝ボーダーが平均7.3秒(当時NR10相当)とかいう超ハイレベルだったり。
解法についてですが、世界、日本共に、トップ層は7-simul使用者が多数を占めるようになってきました。Tommyとかbpaulとか7sfndmw4lmとかいろいろありますが、「7手で揃う」という概念そのものが強いのは間違いありません。
7-simulはほぼ完成された解法で、クロックの理論値と言っても過言ではありません。そのためか、クロックという競技は「終わった」と言われることもあります。同じスクランブルに対してできるアプローチがほぼ1通りであり、いかに速く指を動かすかorいかにラッキースクランブルを引くか、という競技性に変わってしまったためです。
今日はクロックって実は終わってないんじゃないか?という話をします。
同じスクランブルに対してできるアプローチがほぼ一通りということは、周りと差をつけるには「解法を選択する」ことしかありません。
出てきたスクランブルによって解法を使い分け、少しでもラッキースクランブルによって解くというわけです。
後述しますが、実はTommyとbpaulを使い分けるのは、ラッキースクランブル云々という意味では特に意味がないです。この二つの7-simulは数学的には全く同一のものだからです。
今回は、解法を使い分けることで意図的にラッキースクランブルを出すための話をします。具体的には「6-simul」についてです。クロックって実は6手で解けるのでは?という話をしています。
7-simulとは?そもそもクロックとは?という方は各所で学んでから本記事に戻ってきていただけると読みやすいかと思います。
全体として、かなり難しい話になってしまいました。大学教養レベル程度の線形代数の知識(+できればちょっとしたプログラミングの知識も)があると理解しやすいと思います。
またクロックの記事のはずなんですが、クロックが手元にある必要はほぼありません。
序章 6-simulを捕まえるための荷造り
7-simulはなぜ可能なのか
今でこそ世界中に使用者がおり、WRや各国のNRを塗り替えまくっている7-simulですが、そもそもなぜ可能なのでしょうか?
クロックには、揃えるべき文字盤が裏表合わせて18個あり、コーナーの4つは表と裏でつながっているため、パーツの数は14個です。
そのため、これらのパーツを1つずつ順に揃えていくと、14手ですべてのパーツを揃えることができます。
普通のフリップ解法でやっているのは基本的にこれです。
※本記事における「1手」とは、
1.4つのピンの位置を決定する
2.ダイヤルを一つ選び、任意の目盛り分回す
のセットのことを指します。
クロックにおいて、ピンが上がっている部分とピンが下がっている部分のダイヤルは独立に同時に回すことができます。試しに左2つのピンだけを上げた状態で、左上のダイヤルと右上のダイヤルを同時に回してみてください。お互いに干渉しないので、同時に独立に回せることがわかります。
同時に回せるということはすなわち、一度に2手分回せるのです。先ほどの話と合わせると、「一度に2手分回す」を7回行えば、実質14手回したことになり、クロックが揃うのでは?という発想が出てきます。
具体的には、
「7通りのピンの配置であって、その配置で回せる計14通りの操作によってクロックを解くことができるものが存在するか?」
という問題になります。
この考え方自体は割と古くから考えられており、原理的には7手で解ける、ということはかなり昔に証明されています。2022年後期から2023年にかけて、人間にも15秒で可能な方法で、7手で解く方法がアルゴリズムとして提案されました。時代の変革ですね。
クロックのGod's Numberは12
God's Numberとは、「最悪パターンにおける最短手数」のことです。そのため、「God's NumberがNである」ということは、「どのような盤面を渡されても、最善を尽くせばN手以内で解ける」ということを意味します。日本語で「神の数字」ということもあります。
先ほど、クロックは14手で揃えることができると述べましたが、実はクロックのGod’s Numberは12であることが知られています。クロックはどんな盤面からでも12手で揃うということです。
クロックは数学的に完全に解析されているので、証明された結果として単に受け入れてもいいのですが、直感的に理解することもできます。
クロックのある文字盤の取りうる状態は、0時~11時の12通りです。鳩ノ巣原理により、どのような初期状態にいおいても、14個のパーツのうち少なくとも二つは他のいずれかのパーツと同じ状態になっています(厳密性は略)。言い換えると、14個のパーツのうち2つは初めから揃っていると解釈することができます。
よって、2つを除いた12個を順に揃えていくことを考えると、God’s Numberが12であることが直感的に理解できます。ちなみに、数学的に厳密に証明するのもそこまで難しくないです。
6-simulとは
さて、ここまでを振り返ってみると、
・本来14手かかるところを、同時回しによって半分の7手で揃えられる
・実は、クロックは最善を尽くせば12手で揃う
ということになります。
ここで、もしかして、
「最善を尽くせば12手で揃う。さらに同時回しすれば半分の6手で揃う」
のではないか????と思いませんか?※1
今回は、数学とコンピューターの力を借りて、
クロックの究極ともいえる「6-simul」について考えていきます。
※1:いきなり話の腰を折るような話ですが、これは残念ながら偽です。どうあがいても7手かかるようなスクランブルが存在します。こちらは第三章で証明しています。
第一章 すべての7-simulを網羅する旅
6-simulについて考えるにあたり、まずは7-simulについて考えます。6-simulは、7-simulのうち1手がスキップしたものと考えることができるため、7-simulの全容を把握することが重要です。
本章では、存在する7-simulを見つけ出すことが目標です。
クロックはベクトルである
クロックとは何でしょうか?
N×N×Nのキューブは群論である、というのを聞いたことがある方は多いのではないでしょうか?キューブはパーツの置換を繰り返して解くことができるという意味で、群論的であると言われます。
クロックは少し性質が異なります。クロックは、14個の独立に回転可能なパーツからなるパズルで、これらのパーツを操作する順番を入れ替えても、最終的な配置に変化はないという特徴があります。この特徴は数学的に「クロックは14次元のベクトルで表現できる」と言い換えることができます。
クロックの盤面をベクトルで表現する
では、実際にクロックをベクトルの形で表現してみます。
まず、クロックの14個のパーツに順番を付けます。
要素の順番はどう決めてもいいのですが、本記事の中では以下の画像の通りに採番します。以下、黒面(画像左)が表ということにします。

コーナーは表と裏でつながっているので、どちらか一方だけを採番すればよいです。
ここで例えば、以下の盤面は、$${ (0,8,6,2,6,4,7,6,8,1,10,2,10,5) }$$と表現できます。順番通りに針を読み取って並べただけです。なお、「盤面」にはピンの状態は含まないことにします。

「操作」をベクトルの形で表現する
盤面と同じように、操作もベクトルで表現できます。
URピンだけを上げた状態で右上ダイヤルを+1だけ回すと、先ほどの採番における$${ 2,3,5,6 }$$のパーツが+1だけ動いています。よって、この操作をベクトルで表すと、$${(0,1,1,0,1,1,0,0,0,0,0,0,0,0)}$$となります。
次に、同じピンの状態で左上ダイヤルを+1だけ回すと、$${1,7,9,10,11,12,13,14}$$が動いています。$${10,11,12,13,14}$$は反時計回りに動いていることに注意すると、この操作のベクトルは$${(1,0,0,0,0,0,1,0,1,-1,-1,-1,-1,-1)}$$と表現できます。
あるピンの状態におけるクロックの操作の方法は「Upダイヤルを回す」「Downダイヤルを回す」の高々2通りです。
ピンの状態は$${2^4 = 16}$$通りなので、ある盤面に対して行うことができる操作の最小単位は高々32通りです。クロックに対して行うことができるすべての操作は、この32個の操作の組み合わせによって表現できます。
ではこの32通りを先ほどのようにベクトルにしていきましょう。16通りのすべてのピンの状態に対して、Upダイヤルを回したとき、およびDownダイヤルを回したときの時計の動きを書き下します。
これは気合いです。32個くらいなら何とかなるという気合いが数学には重要です(?)。
以下、ピンの状態及び操作を表す記法として以下を導入します。
ピンの状態を表す記法:$${ m_{0100} }$$
操作を表す記法:$${ m_{0100u} }$$
共に添え字の4桁の数字は、どのピンが上がっているかを示しています。ピンの順番はUL,UR,DL,DRの順にします。
操作を表す記法の添え字末尾のアルファベットは、Upダイヤルを回すかDownダイヤルを回すかを示します。Upならu、Downならdです。
つまり、$${ m_{0100u} }$$は、「URピンのみが上がった状態でUpピンを回す」という操作のことを指します。
※記法に使う「m」は「manipulation」の頭文字を取りました。
以下が32通りの操作のベクトル表現です。気合いで書きました。
$$
m_{0000u} =(0,0,0,0,0,0,0,0,0,0,0,0,0,0)\\
m_{0000d} =(1,0,1,0,0,0,1,0,1,-1,-1,-1,-1,-1)\\
m_{1000u} =(1,1,0,1,1,0,0,0,0,0,0,0,0,0)\\
m_{1000d} =(0,0,1,0,0,0,1,0,1,-1,-1,-1,-1,-1)\\
m_{0100u} =(0,1,1,0,1,1,0,0,0,0,0,0,0,0)\\
m_{0100d} =(1,0,0,0,0,0,1,0,1,-1,-1,-1,-1,-1)\\
m_{1100u} =(1,1,1,1,1,1,0,0,0,0,0,0,0,0)\\
m_{1100d} =(0,0,0,0,0,0,1,0,1,0,-1,-1,-1,-1)\\
m_{0010u} =(0,0,0,1,1,0,1,1,0,0,0,0,0,0)\\
m_{0010d} =(1,0,1,0,0,0,0,0,1,-1,-1,-1,-1,-1)\\
m_{1010u} =(1,1,0,1,1,0,1,1,0,0,0,0,0,0)\\
m_{1010d} =(0,0,1,0,0,0,0,0,1,-1,-1,-1,0,-1)\\
m_{0110u} =(0,1,1,1,1,1,1,1,0,0,0,0,0,0)\\
m_{0110d} =(1,0,0,0,0,0,0,0,1,-1,-1,-1,-1,-1)\\
m_{1110u} =(1,1,1,1,1,1,1,1,0,0,0,0,0,0)\\
m_{1110d} =(0,0,0,0,0,0,0,0,1,0,-1,-1,0,-1)\\
m_{0001u} =(0,0,0,0,1,1,0,1,1,0,0,0,0,0)\\
m_{0001d} =(1,0,1,0,0,0,1,0,0,-1,-1,-1,-1,-1)\\
m_{1001u} =(1,1,0,1,1,1,0,1,1,0,0,0,0,0)\\
m_{1001d} =(0,0,1,0,0,0,1,0,0,-1,-1,-1,-1,-1)\\
m_{0101u} =(0,1,1,0,1,1,0,1,1,0,0,0,0,0)\\
m_{0101d} =(1,0,0,0,0,0,1,0,0,-1,0,-1,-1,-1)\\
m_{1101u} =(1,1,1,1,1,1,0,1,1,0,0,0,0,0)\\
m_{1101d} =(0,0,0,0,0,0,1,0,0,0,0,-1,-1,-1)\\
m_{0011u} =(0,0,0,1,1,1,1,1,1,0,0,0,0,0)\\
m_{0011d} =(1,0,1,0,0,0,0,0,0,-1,-1,-1,-1,0)\\
m_{1011u} =(1,1,0,1,1,1,1,1,1,0,0,0,0,0)\\
m_{1011d} =(0,0,1,0,0,0,0,0,0,-1,-1,-1,0,0)\\
m_{0111u} =(0,1,1,1,1,1,1,1,1,0,0,0,0,0)\\
m_{0111d} =(1,0,0,0,0,0,0,0,0,-1,0,-1,-1,0)\\
m_{1111u} =(1,1,1,1,1,1,1,1,1,0,0,0,0,0)\\
m_{1111d} =(0,0,0,0,0,0,0,0,0,0,0,0,0,0)\\
$$
実際のパズルでは$${m_{1111d}}$$(すべてのピンを上げた状態で、下がっているダイヤルを回す)と$${m_{0000u}}$$(すべてのピンを下げた状態で、上がっているダイヤルを回す)は不可能な操作のため、零ベクトルを割り当てています。
互いに独立な操作を選ぶ
「クロックを解く」ということは、与えられたクロックの盤面ベクトルを先ほど書き下した操作ベクトルの線形結合で表現するということです。
盤面ベクトルは14次元なので、可能な30個の操作のうち少なくとも14個の操作を選ぶことで実現できます。
7-simulによって使用できる操作は7×2=14個なので、ちょうど14個の操作によって解くことができる必要があります。
より厳密には、
ここで選ぶ14個の操作を$${ M_1, M_2, M_3, \cdots , M_{14} }$$とすると、任意のクロックの状態$${ C }$$に対して整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$が存在して、
$$
n_1 \cdot M_1 + n_2 \cdot M_2 + n_3 \cdot M_3 + \cdots + n_{14} \cdot M_{14} = -C
$$
を満たす。ということになります。これは以下のように書けるため、14個の操作を縦に並べた行列(以下、操作行列と呼ぶ)の逆行列が存在すれば、それを両辺の右からかけることで整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$を得ます。
$$
\left( n_1, n_2, n_3, \cdots , n_{14} \right) \cdot
\left( \begin{array}{c} M_1 \\ M_2 \\ M_3 \\ \vdots \\ M_{14} \end{array} \right)
=-C
$$
操作行列の逆行列が存在することは、14個の操作が互いに線形独立であるための必要十分条件になります。(厳密性は許してください)
また7-simulを構成するには、あるピンの状態に対してUp、Downを両方回す必要があります。例えば選ぶ操作に$${m_{1001u}}$$が含まれていたら、必ず$${m_{1001d}}$$も含む必要があるということです。
すなわち、候補となる14個の操作の選び方は、ピンの状態7個の選び方と言い換えることができます。
ピンの状態は16通りあり、そのうち2通りはUp、Downいずれかが回せないような状態なので、実質14通りです。
よって計算が必要なのは、ピンの状態14通りの中から7通りを選ぶ$${ 14\mathrm{C}7=3432}$$通りです。
この3432通りのすべてに対して、14個の操作が線形独立であるかどうかを調べればよいわけです。手計算でちまちまやってもいいですが、来年とかになってしまいます。ここからはコンピューターの力を借りていきましょう。
実際にやってみましょう。コードは本質でないのでほぼ省略します。
#ちなみに今回は「Apache Commons Math」を使いました。
こんな風に行列式を計算し、行列式が0でない値を取れば線形独立であると判定します。

3432件の候補すべてに対して、行列式を計算し、0でない値をとるかどうかを判定します。

そして結果は272件でした。候補の3432件に対して1割弱くらいですね。
この中には、90度z持ち替えなど、単に対称移動しただけのものの組も含まれます。
見てもなんのこっちゃかと思いますが、以下に一部を示します。

横に並んだ7つのピンの状態について、その7つが7-simulを構成する(可能性がある)ことを示しています。
ちなみにもちろん、最も有名な7-simulである、Tommyの方法に対応するピンの状態も含まれています(106行目)。

余談ですが、よく知られている7-simulのTommy、bpaul、7sfndmw4lmはどれも本質的には同じものです。ピンの状態の組み合わせは同じで、"人力で"どのように揃えるかの順番を変えただけです。
なので実は、「Tommyで解くといまいちだけどbpaulだととんでもないラッキーケース」ということは起こりえません。
真に7-simulを与えるものの選抜
さて、ここまでで7-simul(候補)をすべて洗い出すことができました。
ここまで何度か強調している通り、今見つけた272件はどれも「7-simul"候補"」であり、実際にすべてが本当に7-simulを与える証明にはなっていません。ここで先ほどの議論を振り返ってみましょう。
※※以下再掲※※
14個の操作を縦に並べた行列(操作行列と呼ぶ)の逆行列が存在すれば、それを両辺の右からかけることで整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$を得ます。
$$
\left( n_1, n_2, n_3, \cdots , n_{14} \right) \cdot
\left( \begin{array}{c} M_1 \\ M_2 \\ M_3 \\ \vdots \\ M_{14} \end{array} \right)
=-C
$$
※※再掲ここまで※※
整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$は、「整数」である必要があります。クロックの操作において「右上ピンを+0.5だけ回転」などということはできないためです。
先ほどはなんとなく通り過ぎましたが、操作行列の逆行列が存在するだけでは、整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$が存在することにはなりません。真に整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$が存在するためには、操作行列の逆行列の要素が、すべて整数である必要があります。
ある整数行列について、その逆行列が存在し、逆行列も整数行列であるための必要十分条件は、行列式の値が1または-1となることです。(証明リンク)
では272通りすべてに対して行列式を計算し、その値が1または-1になるものだけを抜粋すればよいわけです。
これは先ほどの独立性を調べるコードで検証可能です。実際に確かめてみたところ、先ほどの272件のうち、真に7-simulを与えるものは268通りであることがわかりました。

というわけで、真に7-simulを与えるものの一覧を置いておきます。何に使うかは知らないです。印刷して冷蔵庫とかに貼るとよいかもしれません。
章のまとめ
まずはここまでお読みいただきありがとうございます。難しい話をしすぎているので、ここまで読んでいるのは1人いるかどうかくらいなのではと思っています。そう、あなたは選ばれた一人です。
さて、ここまでの議論から明らかになった結論は一つで、
「7-simulは268通りある」
というものです。
次章では、この268通りを実際に構築していきます。
第二章 すべての7-simulを作る修行
クロックを解くということ
「クロックを解く」とは、クロックの状態に対して操作行列の逆行列を右からかけることで、整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$を得るということです。
整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$は各状態における「回す量」を示しているので、回すときのピンの状態とピンの回す量がわかれば完璧に解けた、よいというわけです。
ここで、「クロックの状態」は文字化できることを明言しておきます。
クロックの過去記事でも導入した通り、クロックのパーツに以下のように名前を付けます。

例えば、黒面のセンターを上エッジに合わせるために必要なダイヤルは「U-L」と表現できました。今回は、14個のダイヤルすべてをこのような形で表現することで、「クロックが解けた」ということにします。
逆行列からクロックを「解く」
具体的に、クロックを解いていきます。ここでは、皆さんもよく知っている7-simulである、Tommyの方法に対応したピンの組み合わせを使用します。m_{1000},m_{1010},m_{0001},m_{1001},m_{0101},m_{1101},m_{1011}
この7つのピンの状態からなる操作行列の逆行列を計算すると、以下のようになります。(例によって見ただけではなんのこっちゃです)

これを、クロックの状態ベクトルの右からかければよいです。クロックの状態ベクトルを、以下のように書くことにします。
$$
C = \left( \mathrm{UL}, \mathrm{U}, \mathrm{UR}, \mathrm{L}, \mathrm{C}, \mathrm{R}, \mathrm{DL},\mathrm{D}, \mathrm{DR}, \mathrm{u}, \mathrm{l}, \mathrm{c}, \mathrm{r}, \mathrm{d}, \right)
$$
クロックの命名を順番に書いただけのものです。ここに先ほどの操作行列の逆行列を右からかけ算すると、以下の結果を得ます。

整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$を得ることができました。ということは、ピンの状態とダイヤルの量が完全にわかりました。これにて、Tommyのピンの状態において7-simulが「解けた」と言えます。
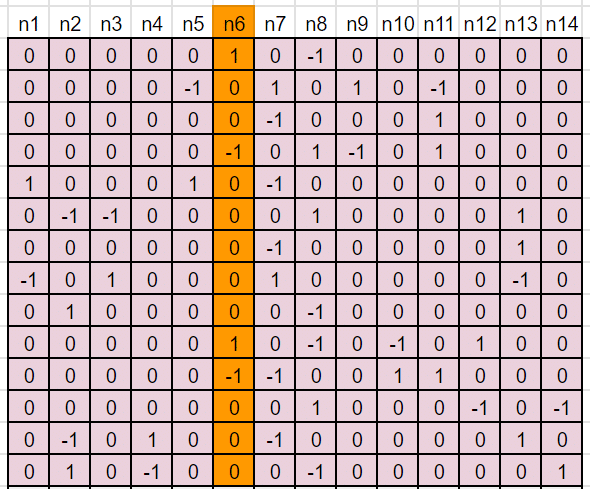
ちなみに、操作行列の逆行列を右からかけ算するのはすごく簡単です。というか、逆行列の見た目から計算するまでもなくわかります。
具体的には、縦の列が一つの整数nに対応しています。例としてn6に対応する欄に色を付けました。この縦の1と-1があるところの文字盤を考えれば、n6を書き下すことができます。
すべての7-simulを「解く」
では次に、268通りすべての7-simulを解いていきましょう。これはコンピュータの力を借ります。ここまでくればあとは結構作業ゲーです。
というわけで解けました。ここにすべての7-simulを解いた結果を置いておきます。寝室の天井とかに貼ってください。

横に並んだ7つのピンの状態は、その7つのピンの状態が7-simulを与えることを示しています。その右に並んだ14個の計算式は、左から順にn1,n2,…,n14の計算式です。これで、好きな7-simulを選んで解くことができるようになりましたね。
<余談>最強の7-simulはTommyの方法という話
現状、世界で最も良いとされている7-simulはTommyの方法です。bpaulに比べて何が良いかというと、「見ながら回すパートが簡単」というのがあります。
先ほどの整数$${ n_1, n_2, n_3, \cdots , n_{14}}$$のうち、Tommyの7-simulで記憶文字となっているのはn7~n12の6つです。

14個の中でも特に計算量の多いn7とn8を計算して覚えてしまおうというのですから、その分実行はわかりやすくなります。
bpaulの方法ではn7、n8の代わりにn13、n14を覚えます。インスペクションで計算する量が減る代わりに、実行がやや複雑になります。
章のまとめ
ここまで読んでくれている人いますか?ありがとうございます。
本章の結論は「268通りすべての7-simulが解けました!」です。
第三章 6-simulに迫る冒険
ここまでで、すべての7-simulを解くことができました。とうとう、6-simulを見つける冒険に出かけましょう。
すべての7-simulで解いてみる
サンプルとして以下のスクランブルを使用しましょう。
UR5- DR2- DL6+ UL6+ U4+ R0+ D4- L2+ ALL1- y2 U3- R5- D0+ L4+ ALL3+

状態ベクトルは$${( 6,11,8,4,11,7,2,2,7,6,1,6,4,1 )}$$です。このスクランブルに対して、先ほどの268通りの7-simulで解くとどうなるか、結果はこちらです。一部だけ示しています。

よくわからん数字が並んでいますが、3行目を見ると、n11=n12=0となっています!n11とn12は同じピンの状態で回す2つのダイヤルなので、ピンの状態一つが丸ごとスキップ=6-simulということになります。
実際にNo.3の7-simul(以下)で解くと、ピンの状態m_{0011}における操作がスキップし、6-simulで解けることが確認できます。

7-simulかかるときもある
ここまで期待されている方には残念なお知らせですが、初期状態によっては、どの7-simulを使ってもきちんと7手かかることがあります。
ランダムなスクランブルに対して、最も手数が少なくなるようなときの手数を10000回分計算しました。

ほとんどの場合は6-simul、3割程度が7-simulで解けるということです。
そのため、「毎回6-simulで解く」はそもそも不可能です。以下、特殊な場合について、6-simulで解くための方法について考えていきます。
エッジとセンターが揃っている場合
エッジとセンターが揃っている場合、以下のような場合を考えます

先ほど「特殊」と言いましたが、このようなスクランブルはちょうど50%位の確率で出現します。
センターとくっついているエッジがUに来るように持ち替えます。ここではz2です。先ほどの7-simul一覧には、すべての持ち替えを考慮したものが含まれているので、Uエッジ=センターとなるように持ち替えてしまって問題ないです。
先ほどの表から、-U+C or +U-C を含むものを列挙します。これにより、少なくとも1つのスキップが発生することが保証される7-simulを絞ります。

150個ありました。全268個中150個ということで、体感かなり多いです。それほど、「エッジとセンターが揃っている」というのはラッキーケースの要因になるということですね。
次に、-U+Cのもう片方にあたるダイヤルの計算式を抜き出して観察してみます。全部で28通りありました。

さらに今、-U+C=0が成り立つので、代入できるところには代入して、計算式はこのように変わります。

ここで、代入によって重複したものをグレーアウト、さすがに人力で計算するのは現実的でないものをワイン、とても練習すれば何とかなりそうだけどいったんやめておくものをチーズで色付けしました。
残りの、割と楽に人力で計算できそうなものを太字で強調しています。
具体的には、
1.-c+d(c to d)
2.-l+d(l to d)
3.-r+d(r to d)
4.+u-l-c+d(l to u + c to d)
5.+u-c-r+d(r to u + c to d)
6.+UL-L-l+c(L to UL + l to c)
7.+UL-L+u-l(L to UL + l to u)
8.+UR-R+c-r(R to UR + r to c)
9.+UR-R+u-r(R to UR + r to u)
が残りました。この9通りを確認し、もしその値が「0」になるところがあれば、先ほどの-U+Cと併せて、同じピンの状態に対して2つのダイヤルがともに0になることになり、そのピンの状態はスキップします。
よって、6-simulで解けるというわけです。
この9通りすべてを試して、少なくとも1つの値が0になる確率は約54%です。エッジとセンターが揃っている確率と合わせて、約27%の確率で6-simulを使うことができることが示されました。
さらに、スクランブルによっては、エッジとセンターが揃っている場所が複数あることがあります。そのようなときも考慮すると、約32%の確率で6-simulが可能です。
エッジとエッジが揃っている場合
次に、エッジとエッジが揃っている場合を考えます。エッジとエッジの位置関係は隣接と対面の2通りありますが、ここで考えるのは隣接です。以下のような場合です。

例によって持ち替え可能です。揃っている2つのエッジがUとRに来るように持ちます。この場合はz'です。
先ほどの表から、+U-Rを探しましょう。結構ありました。

この時の、+U-Rの相方になっているものを抜粋します。過程は省略し、「人力で計算するのが現実的なもの」のみを示します。以下の4つです。
1.-c+r(r to c)#エッジセンタースキップと重複
2.-u+r(r to u)
3.+l-c+r-d(c to l + d to r)
4.-u+c+r-d(u to c + d to r)
この4つのうち少なくとも一つが0になれば、そのピンの状態がスキップし、6-simulで解けるというわけです。
エッジとエッジが揃っているような場合が出現し、なおかつ上の4通りのうち少なくとも1つが0になるようなスクランブルの出現確率は約18%です。
エッジとセンターが揃っていて、6-simulで解ける場合と、エッジとエッジが揃っていて6-simulで解ける場合のうち、少なくとも一方に当てはまるパターンが出現する確率はおよそ41%です。
よって、上記のすべてを行うことで、41%の確率で6-simulで解くことができることになります。
章のまとめ
ここまできたら最後まで読んでほしいです。
本章の結論は「人力で、41%の確率で6-simulで解ける!」です。
第四章 6-simulを構築する最終決戦
前章までで、特殊な場合に限り6-simulができるのではないかという可能性について考えました。
本章では実際に、6-simulを構築していきます。
※ ここでクロック、7-simulに詳しい方にお願いです。ここから出てくる7-simulは、理論上(14文字記憶によって)7手で解ける方法ですが、執筆時点でこれらを6文字以内の記憶で人力で解くアルゴリズムは発見できていません。これらを具体的なアルゴリズムに書き下すことができた方はぜひご一報ください。ちょっといい景品とかはお渡しします。
エッジとセンターが揃っている場合
UエッジとCセンターが揃っている場合、以下のいずれかが0になっていればよいということを示してきました。
1.-c+d(c to d)
2.-l+d(l to d)
3.-r+d(r to d)
4.+u-l-c+d(l to u + c to d)
5.+u-c-r+d(r to u + c to d)
6.+UL-L-l+c(L to UL + l to c)
7.+UL-L+u-l(L to UL + l to u)
8.+UR-R+c-r(R to UR + r to c)
9.+UR-R+u-r(R to UR + r to u)
ではこの9つが0だった時に、具体的にどのような操作によって6-simulが可能なのでしょうか?一つずつ見ていきましょう。
1.-c+d = 0
以下のピン構成の7-simulを使用すると、m_{0011}がスキップします。
m_{1000}m_{0100}m_{1100}m_{0110}m_{1110}m_{1101}m_{0111}
ダイヤルの計算式は以下です。

前述の通り、ではこれを具体的にどう解くのかは確立されていません。8文字記憶すれば可能であることが証明されましたが、n4を記憶する必要があり、人力で可能と言えるかどうかは怪しいです。
2.-l+d(l to d)
以下のピン構成の7-simulを使用すると、m_{0011}がスキップします。
m_{1000}m_{0100}m_{1100}m_{0110}m_{1110}m_{0011}m_{0111}
ダイヤルの計算式は以下です。

色々と研究した結果、これは比較的人力で解ける可能性がありそうです。これについてはいつか解説できるかも、、
3.-r+d
これは2.の左右対称で解くことができます。
4.+u-l-c+d
以下のピン構成の7-simulを使用すると、m_{0011}がスキップします。
m_{1000}m_{0100}m_{1010}m_{1001}m_{1101}m_{0011}m_{0111}
ダイヤルの計算式は以下です。

これは今のところ、「人力では無理」という結論になりそうです。もし発見した方がいたら僕が大喜びします。
5.+u-c-r+d
これは4.の左右対称で解けます。
6.+UL-L-l+c
以下のピン構成の7-simulを使用すると、m_{0001}がスキップします。
m_{1000}m_{1100}m_{1110}m_{0001}m_{1001}m_{0101}m_{1011}
ダイヤルの計算式は以下です。

これはおそらく人力で行けます。いつか解説します。
7.+UL-L+u-l
これは、このまま実行開始面となるようにTommyで解くとm_{1010}(6step目)がスキップします!うれしいですね。
#Tommyの7-simulについては以下を参照!(ここまで読んでくれている人で今更Tommy知らない人はいないとは思っています。)
8.+UR-R+c-r
これは6.の左右対称で解けます。
9.+UR-R+u-r
これはTommyの左右対称をやると6step目がスキップします。Tommyの左右対称は、Tommyできる人なら結構簡単に習得できます。筆者はいらん事したがりなので、bpaulの左右対称ニュートラルとかやってました。
エッジとエッジが揃っている場合
エッジとエッジが揃っているとき、6-simulをやるには以下の4通りの選択肢があります。
1.-c+r(r to c)#エッジセンタースキップと重複
2.-u+r(r to u)
3.+l-c+r-d(c to l + d to r)
4.-u+c+r-d(u to c + d to r)
この内1.についてはエッジとセンターが揃っているとき、と重複しています。よって2.以降を考えれば十分です。
2.-u+r
これは、zと持ち替えた状態が実行開始面となるように、Tommyをやればよいです。これに関しては、すでに無意識にできている人が多いのではないでしょうか?
運よく6-simulになった!というときは結構このパターンが多いと思います。
3.+l-c+r-d
以下のピン構成の7-simulを使用すると、m_{1010}がスキップします。
m_{0100}m_{1100}m_{0010}m_{1010}m_{0110}m_{1011}m_{0111}
ダイヤルの計算式は以下です。

これもどうにかなります。いつか解説します。
4.-u+c+r-d
以下のピン構成の7-simulを使用すると、m_{1010}がスキップします。
m_{0100}m_{0010}m_{1010}m_{0110}m_{1110}m_{0101}m_{1011}

これはほぼ解明しています。今度解説します。
章のまとめ
ここまで読んでいただき、本当にありがとうございます。質問があればDMやリプライでいただくか、どこかでお会いしたときに直接聞いてくれれば早口で語り始めます。
本章の結論は「41%の確率でできる6-simulを構築しました。ただし具体的なアルゴリズムは未発見です」ということです。アルゴリズムは未発見なので今現在6-simulで解くことはできませんが、逆に言うと、いつかアルゴリズムが発見された際には、この方法で6-simulができるようになります。
これからも7-simulについて研究を続ける予定なので、気長にお待ちいただければ幸いです。
最終章 クロック討伐
クロックの最終形態について
7-simulの台頭により、「クロックは7手で解ける」ということは広まりました。また本記事で、「毎回6-simulで解くことは不可能」ということを証明しました。
これらの事実から、「7-simulはクロックの最終形態」という結論を導き出すことができるかもしれません。
そういった意味で、Tommyの7-simulは「クロックを討伐した」と言っても過言ではありません。なぜなら、7-simulの中でも、Tommyの方法は”最適”だからです。
第二章の余談で、Tommyの方法は「計算が一番難しい所を記憶文字にする」という所がポイントと述べました。
ここで、計算が難しい所を先にインスペクションで処理して、実行を簡単にしたいという主張は納得できます。ただ、全体としてもっと計算量が少ない7-simulを使えばよいのでは?と思いませんか?理論上はそうです。
しかしここで驚くべき点は、実はTommyの方法は268通りすべての7-simulの中で最も計算量が少ないピンの組み合わせを採用しています。
最も計算量が少ない7-simulを使用し、その中でも比較的計算量が多い操作を記憶文字に変換し、実行を簡単にするという意味で、Tommyの方法は全7-simulの中で最も良い方法と言えます。
毎回6-simulは不可能、という前提があるので、最適な7-simulであるTommyの方法はまさに「クロックを討伐した」ということができます。
討伐完了。次の時代へーー
では、Tommyをもってクロックの討伐は完了したのでしょうか?色々と語ってきましたが、自分は「半分Yes」だと思っています。
今回、41%の確率で6-simulができるという話をしましたが、そもそTommyの方法は黙っていても5%くらいの確率で6-simulになります。なので少なくとも単発記録に関しては、Tommyにおけるラッキースクランブルによって達成できるラインがMaxなのではと思っています。
平均に関しては、6-simulの可能性があると思います。41%の確率で6-simulということは、5回中少なくとも4回6-simulで解ける確率は10%程度あります。
10%の確率で、6-simulのao5を残せると考えれば、この先もし万が一、上で紹介した複雑な7-simulが全部解明され、それらをすべて使いこなし、それらをすべてTommyと同じ練度まで上げ、インスペクションで6-simulを判断し、爆速で回すことができる超人のもとに、10%の確率で訪れるスクランブルセットがやってきたとき、クロックの平均記録が「終わる」のではないでしょうか。
クロック戦記
本研究の歩み
ここまで読んでいただき、本当にありがとうございます。
かなり長い記事になってしまいました。
また、ここまでくる道のりも長かったです。
本記事の発案は2023年10月ごろで、クロックのGod’s numberが12という話を聞いて、「もしかして6-simulできるんじゃね??」と思ったのが始まりでした。
実はその時は少し考え、「どんなスクランブルに対しても6-simulが可能」であると思っていました。道筋も見えていたつもりでした。
2023年のアドカレのネタにしようと思い研究していましたが、2023年11月末ごろにこれまでの自説がひっくり返され、「どうあがいても7-simulかかるスクランブルがある」ということを発見しました。アドカレ断念、、CPファーストの話でお茶を濁しました。
当時は具体的な7-simulを書き下すことはせず、あくまで数学的にはどうのこうのという話をしていましたが、どうせ6-simulが無理なら、、と思い、すべての7-simulを具体的な操作として書き下すことにしました。
2023年12月からは具体的な7-simulを網羅する方法を考え始めました。ロードマップとかも書きました。
2024年3月ごろ、大方の結果が固まりました。後は、まだ解明されていない7-simul5種を何とか人力でも解けるようにアルゴリズム化するだけです。
、、ところがこれが無理でした。さすが、Tommyの方法が出てくるまでに5年以上かかっただけのことはあります。妥協し、アルゴリズム化は読者への課題としましょう。
2024年5月、ゴールデンウィークに執筆開始。
2024年5月10日、完成・公開
あとがき
いやぁ、、、不可能でしたね、6-simul。
可能性あると思ってたんですけどね、、、
2023年6月ごろからクロックに手を出し始めて、もうすぐ一年ですね。なにはともあれ、この記事をもっていかのおすしのクロック研究は一段落としようと思います。
今度はまた別の種目や解法について、深いところまで考えてみたいですね。
CPファーストでFMCとかできないかな。CPなら黙っててもまあまあの確率でスキップするからあんまりメリットないか。
それではまたーー
本研究の量的評価
書いたコード:3442行
作ったスプレッドシート:41枚
研究期間:7か月
この記事が気に入ったらサポートをしてみませんか?
