
「べき分布」で考える株式投資
僕はこれまで自分の投資法として「株価は読まない」というスタンスを堅持してきました。株価を読むアプローチは下記のような様々なものがありますが、
・需給で判断する
・織り込みを見極める
・チャートの形
・移動平均線/ボリンジャーバンド など
どれも根拠が曖昧/脆弱だったり、アノマリーと呼ばれる一定期間は有用だがみんなが知るまでしか賞味期間がないものばかりで、自分の投資判断に含めてもプラスにならないと考えてきたからです。
そんな中、最近「経済物理学」と呼ばれるユニークなアプローチがあることを知りました。何年眺めつづけていても確たる法則性が見いだせない株価の動きですが、実は一定条件における物理現象と同じ振る舞いをしているらしいです。
この世界を切り開いた人がベノア・B・マンデルブロさんという方です。雪の結晶、海岸線、ブロッコリー、地震、収入分布、株価など、物理学だけではなく社会学から経済学といった様々な範疇に入る事象が共通の一つの大きな法則で考えることができることを発見しました。マンデルブロさんはこれを「フラクタル」と名付け、この法則に当てはまるものが「べき分布」という分布になることがわかっています。そしてこの発見を機に、経済と物理学をくっつけようという考え方が生まれ「経済物理学」と呼ばれる領域が誕生したのです。
「株価を物理現象として捉えてみる」
なんだか株価の普遍的な法則が見える気がしませんか。この記事はそんな「フラクタル」な「べき分布」についてまとめたものです。
1.株価は「正規分布」ではなく「べき分布」
現在の金融工学は商品の価格変動は「正規分布である」という仮定をもとに発展してきました。「95%の確率でこの範囲に留まる」といった表現や「ブラック-ショールズの方程式」をベースにした様々なデリバティブ商品などはすべて正規分布であるはずという仮定から生まれています。
しかし、実際の株価データを調べてみると、株価は正規分布ではなく「べき分布」と呼ばれる別の分布をしていることがわかっています。
例えば、2008年のリーマンショックの下落は正規分布の計算値だと「14京(140,000,000,000,000,000)年に一度」にしか起きない希少事例ということになってしまいますし、「ブラック-ショールズの方程式」でノーベル賞を受賞したショールズさんらを招聘して運用したヘッジファンド「LTCM」も、正規分布の仮定の上に高度な計算を重ねてしまったため、計算上ありえないはずの大きな価格変動に飲み込まれて破綻しました。べき分布は正規分布よりも激しい動きをするので、前提を間違えるとリスクを大きく見誤ることになるのです。
もう一つ。株価が正規分布ではなくべき分布であるということは、「サイコロを振るような単純なランダムウォークとは違った原理」で動いているということになります。
例えばサイコロを100回振ったときの和の分布はを3500(3.5×100回)を中心とした正規分布になりますが、このサイコロのように「過去の値が今回の値に影響を与えない。そしてランダム」という原理で動くものは正規分布になります。
しかし株価が正規分布ではなくべき分布であるということは、株価はこの原理では動いていないということなります。では、その「違った原理」とは一体どんなものなのでしょうか。これはべき分布が現れるときの物理的な特徴を追っていくことで輪郭が見えてきます。
そもそも「べき分布ってなんなの?」というところから順に説明していきます。
2.基礎知識:正規分布とべき分布
まずは基礎知識として正規分布とべき分布について説明します。
正規分布
世の中のデータ分布として最も有名なのは「正規分布」です。ベルカーブとも呼ばれる中心値を頂点とした分布で、身長や学力を始めとした様々な事象でこの分布が確認されています。学力などで使われる偏差値は中心を50として、1σ(シグマ)を10となるように算出した指標です。偏差値70というのは中心より2σ離れた値ということで、上位2.2%にいることを表します。
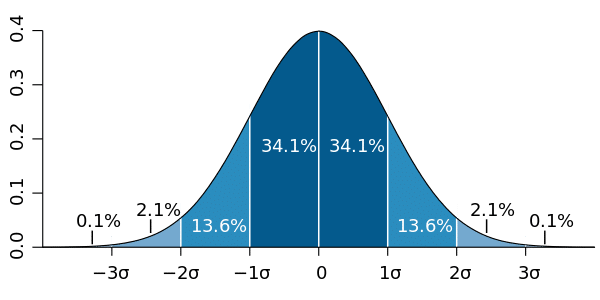
べき分布
今回の主役である「べき分布」は、正規分布ほど有名ではありませんが、これも世の中の様々な事象で観測される分布です。
・地震の分布
・雪崩(雪玉の大きさ)の分布
・年収の分布
・Webサイトの大きさ(リンク数)の分布
・都市の大きさの分布 など
がこの分布になります。株価の変動の大きさもべき分布です。べき分布の分布イメージを掴んでもらうには「ガラスのコップを割ったときの破片の分布」を想像してもらうと良いと思います。ガラスを割ったことがある人であれば「ガラスの破片の分布」は以下のようになることが想像できるのではないでしょうか。
粉のような極めて小さいかけらが、最も多く発生
それよりもすこし大きい欠片が、多く発生
それよりも大きい欠片が、少し発生
・・・・
一番大きな巨大な欠片が、1個
この分布をグラフにすることこんな感じになります。

ガラスの破片の分布と言われると、なんだかランダムで規則性が無いように思えるのですが、実はこの「べき分布」という強い規則性をもった分布になることがわかっています。さらにこの「グラフの両軸を対数軸」に変えるとこのべき分布はもっとユニークな形で捉えることができます。

べき分布グラフの両軸を対数表記に変えるとなんと直線になります。
両対数グラフで直線ということは、「どの区間で見ても、大きさがX倍になると頻度がY倍になる」という性質があるということを意味します。
過去の実験では「じゃがいもを凍らせたもの」の破片の分布が、どの区間を見ても「重さが2倍になると発生頻度は1/6」という計測結果もあります。また、最も有名なべき分布である「地震の揺れの分布」は、グーテンベルグ・リヒター則という名前がついており、「どの区間でみても、地震の規模が2倍になると発生頻度は1/4」ということがわかっています。
3.正規分布とべき分布の比較
正規分布とべき分布。この2つの分布を同じグラフ上で比較すると以下のようになります。

図のようにだいたい2σぐらいまでは同じような形になっており、株価の変動でいうと「通常の値動きのとき」はおおむね似ています。
一方、グラフの端っこ(3~4σ以降)を見比べると、正規分布では「ほぼ出現率がゼロ」になるようなところでも、べき分布の場合はデータが出現しています。リーマンショックは14京年に一度の出来事という計算値になってしまうのはこの分布の違いによるものです。
べき分布は両対数にすると直線になると書きましたが、両対数グラフ上で2つの分布を書くとこのようになります。
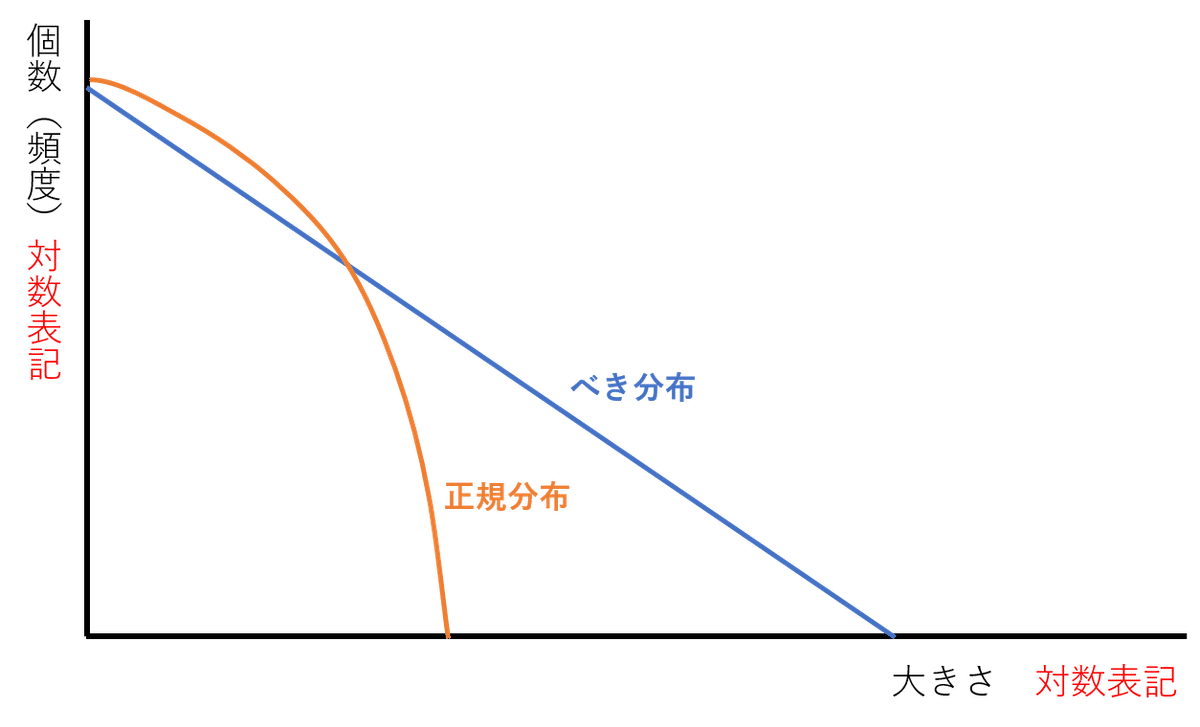
べき分布が直線である一方で、正規分布は下向きのカーブを描きます。この表記もよく登場するのでイメージを掴んでおいてください。
進撃の巨人の世界
「どちらの分布でも大した違いはないじゃん」と思った方もいらっしゃると思いますが、この分布の違いを日常生活、例えば身長の分布で考えてみるとその違いがわかります。
人間の身長は正規分布です。平均値が170cmぐらいで、180cmの人が少しいる。2mを超えるような人は人生で何回か会う程度しかいないという感じだと思います。そして3mを超える人は地球上に存在しません。
ところがもしこれが「べき分布」だったらどうなるでしょうか。べき分布の世界を図にするとこんな感じです。

べき分布の場合は、小さい人がたくさんいる一方で、2mを超えるような人も一定数いて、さらに3m、4m、5m、それ以上の人もいるという世界になります。まるで進撃の巨人の世界です。
正規分布の世界(現実の世界)では、乗り物もせいぜい2mぐらいの人しかいないという前提で設計されていますが、べき分布の世界ではそういうわけにいきません。またバスケットボールやバレーボールといったスポーツも、現行のルールでは成り立たなくなります。
そして何より「べき分布の世界」は、小さい人たちよりも少数の大きな人が注目される世界だと気づくと思います。
例えば、地震は普段から起こっている小さな地震は注目されず、時折起こるM7.0を超えるような大地震だけが大きな注目を浴びます。Webサイト(の大きさ)もべき分布ですがGoogle、Amazonといった巨人サイトは、Web界の王様のような影響力を持っています。
このようにべき分布の世界は、驚くような巨人がたまにいて、その人達が注目されるような世界といえます。
リーマンショックを予測していたということで一躍有名になったナシーム・ニコラス・タレブさんの「ブラック・スワン」では、この2つの世界を「月並みな国(正規分布)」と「果ての国(べき分布)」という表現を使って、株式市場を月並みな国だと思い込んでる金融関係者たちを全編に渡って否定しています。
4.実際の株価データで見る
S&P500の分布
それでは実際の株価データで見てみましょう。この図は田淵直也さんという方の著書からの引用です。

このグラフはS&P500の騰落率の分布を示しています。
グラフを見ると実際の株価は概ね正規分布に沿っていますが、①〜③のところに違いが見られることがわかります。①と②は投資を行う上では大きな問題がありませんが、③はいわゆる「〇〇ショック」などですので看過すると大変なことになるわけです。
またこの分布を眺めると「正規分布」ではなく、もしかしたら「べき分布」なのではないかと少し疑念が湧くのではないでしょうか。
ダウ・ジョーンズ(対数グラフ)
それではもう一つ。これは前述したマンデルブロさんの著書によるデータです。

こちらはダウ・ジョーンズの分布です。グラフが対数表記になったことで、正規分布ではなく「べき分布」であることが明確になっています。
正規分布内に当てはまる部分が白く、それを超える部分が黒くなっています。そしてグラフは対数軸でほぼ直線になっており、これを正規分布と呼ぶのはさすがに無理があります。
ダウ・ジョーンズとナスダック(対数グラフ)
もう少しデータを並べてみます。これは、ディディエ・ソネットさんの著書のグラフです。
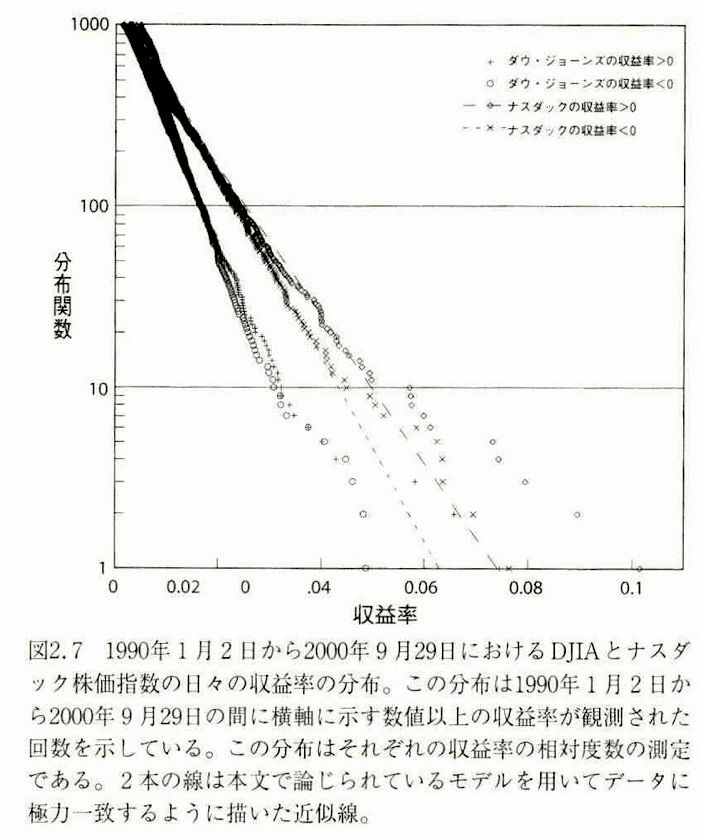
今度はダウ・ジョーンズとナスダック、それぞれプラスとマイナスを分けて4つの系統を表記したものです。これを見ると、
・ダウとナスダックでは直線の傾きが違う
・ナスダックの方が動きが激しい
・プラスとマイナスは概ね同じ傾きだが、ややマイナスの変動のほうが激しい
といった特徴が見えてきます。
日本株の分布(対数グラフ)
最後に日本株のデータです。こちらは増川純一さんらの著書からの引用です。

グラフの下に書いてある数字は株式コードです。このグラフを見ると、
・日本の個別株も「べき分布(直線)」になっている
・銘柄ごとに直線の傾きが違う
・変動率は、8411(みずほHD)など大型株が小さく、4346(ネクシィーズ)などの小型株が大きい傾向
こんなことがわかるのではないでしょうか。
株価の変動は正規分布ではない
ここまで色んなグラフ出しましたが、株価の分布は正規分布ではないことを改めて強調しておきます。
実は、金融機関の中でも「正規分布ではない」ことは、割と常識になっているようなのですが、そのまま受け入れると現代ファイナンス理論が使えなくなってしまうため否定するわけにはいきません。そこで以下のような対症療法的な対応をしているというのが実態なのです。
・大きな変動部分は、正規分布の例外として無視する
・大きな変動部分をファットテールと呼び、正規分布からファットテールを生むような歪なモデル(GARCHモデル等)を使って対応する
・オプション価格は現実の方がブレが大きいため、鉛筆をなめて調整する
※これら金融機関の対応については、前述の「ファイナンス理論全史」を参考にしています。
5.「べき分布」はどういうときに生まれるか
ここまで株価が「べき分布」になっているということを説明してきましたが、ここからはなぜべき分布になるのかを考えます。
べき分布は科学の基礎である物理学で様々な研究がされていて、共通点を見つけることができます。

べき分布に見られる2つの特徴
地震、雪崩、年収分布、Webサイトの大きさなど、べき分布になる現象には実は大きく2つの特徴(共通点)があります。
①臨界状態⇒相転移
②過去が影響する
ここから先は
¥ 1,000
この記事が気に入ったらサポートをしてみませんか?
