パイ。arc と radians

『プロセッシングをはじめよう』を相変わらずなぞっています。
８章の『動き』までなんとなく理解したようなしてないような気で読み進めてましたが、９章『関数』になった途端についていけなくなりました。関数の基礎についての解説なのですが、それまでの章をとりあえずなぞってみたものの、いま自分のやっているもの、打ち込んでいる式がなんなのかが完璧に理解できていないので読んだところで全く頭に入りません。

そこまで行ったところで、また初めから。
わからないところをわからないままにしていたので、今度は「理解」まで行ってみよう。

描く

基礎中の基礎、描画。ここで学ぶのは以下の関数。

size
strokeWeight, strokCap, strokeJoin
point, line
rect, triangle, ellipse, quad, arc, radians

『紙を選ぶ、ペンを選ぶ、好きな場所に図形を描く』
単純に説明するとこれを画面上でやりましょう。ということになります。
これが心的フックかな？

上記の文を関数にすると
紙を選ぶ(size)、
ペンを選ぶ(strokeWeight)
好きな場所に図形を描く(point etc...)

になります。

特に説明もいらないほどの関数ばかりです。座標の２点を指定してそれを結んでくれるのがline　それが３点になるとtriangle　4点がquad
RectとEllipseが似たような条件で基点の座標を指定して、幅(x)と高さ（y)を指定する。

パックマン！

この中で私が躓いたのがarc
円を途中まで描いてその始点と終点が中心点に向かいます。簡単に言うとパックマンみたいな形が描けます。
パックマンの口にあたる部分、この開きをどのように指定するか。
まずarcの基本ルール

arc(円の中心座標x, 円の中心座標y, 円の幅, 円の高さ, 始点, 終点);

Processingではよく使う４つの角度に固有の名前を付けています。
PI, QUARTER_PI, HALF_PI, TWO_PIの４つで、それぞれ
180度、45度、90度、360度に対応します。

時計で言うと、３時からスタートしてぐるっと一周。
本に載っている順で作図していきます。まずはHALF_PI。
０からスタートしてHALF_PIまで、ということは90度。右下の1/4が作図される形。

なるほど。次。
今度は右上1/4がないもの、ちょうどパックマンが口を開けている状態。
０から始まって一番上の270°の位置。

ヨシっ。簡単簡単。次！
今度は左下の1/4が欠けたもの。ってことはPIからスタートして下に戻るからHALF_PIまでだ！

位置の名前じゃありません

あれ？真っ黒。。。。
その時の式

size(500,500);
background(0);
noStroke();
arc(width/2, height/2, 300, 300,PI, HALF_PI);

これがよくわからなかった。ひとつめ、ふたつめまではいけたのになんでこれだけ！？ここで私は勘違いしていました。本に載っていたラジアンと角度、それとProcessingでの名前の対応表を位置の名前だと勘違いをしていました。

どういうことかというと、

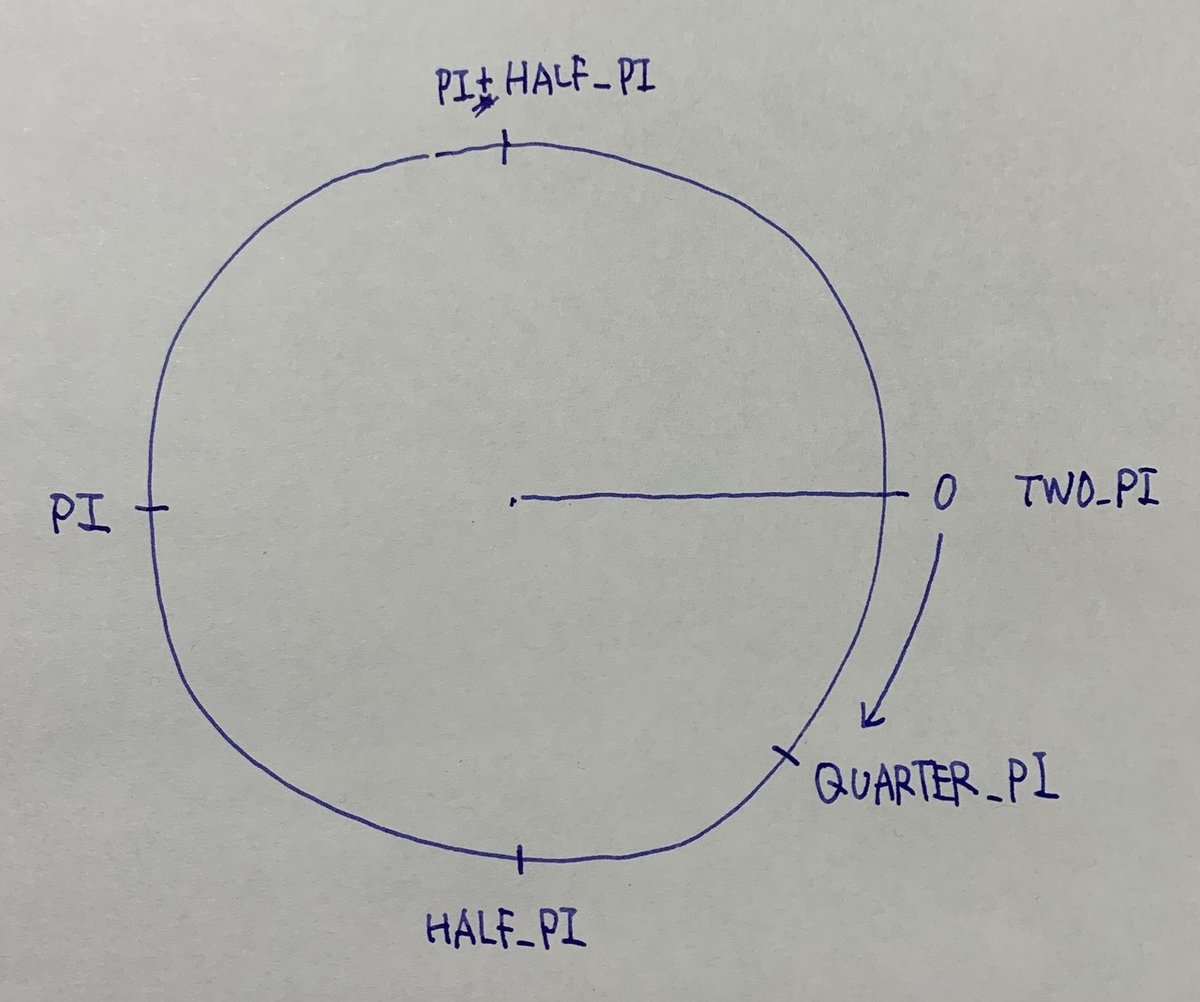
それぞれの角度に対応する位置にこの名前がついている。そう思っていました。
なので考え方はこう。

となると最後のものは、

当然こうなると思っていたわけです。
正しくは

size(500,500);
background(0);
noStroke();
arc(width/2, height/2, 300, 300,PI, TWO_PI+HALF_PI);

0からスタートしたわけではないのでそこを素通りできません。180度がもう180度回転したら（右回り）それは0度ではなく360度なのでTWO_PIにHALF_PIをたさなきゃいけないわけです。
位置の名前として認識していた私は、一番最初のものも0からスタートしてHALF_PIまでなのであればTWO_PIと０は実質同じ位置なので、この関数の最後の部分が(-, TWO_PI, HALF_PI);でも成り立つと思っていました。(もちろんこの式でも画面は真っ黒です。）

続く例もこれに気が付かずに作図できないでいました。

上記と同じ理由です。QUARTER_PIはTWO_PIに足してからじゃないとこの位置になりません。下が正しい式

size(500,500);
background(0);
noStroke();
arc(width/2, height/2, 300, 300,PI+QUARTER_PI, TWO_PI+QUARTER_PI);

radians

どこで気がついたかというとその後の『度を使って描く』でradiansがでてきたところでした。

角度を度で指定したい人はradians()関数を使ってラジアンに変換するといいでしょう。この関数は度で指定した角度を、対応するラジアン値に変えます。

上記の作図をradians()で描くとこうなります。

arc(width/2, height/2, 300, 300,radians(225), radians(405));

ちなみに最初の間違いをそのままradians()で描くと

arc(width/2, height/2, 300, 300,radians(225), radians(45));

225度がなぜか回転していくとなぜか45度に減る。。。これはおかしいですよね。
ここで気がつきました。

ここまで読んで『何言ってんだコイツ？』となった方は正しく理解できている方です。少なくとも私は上記のような思考過程を経て理解することができました。

PI とradians()　完全に理解した！