
【論文要約】RoFormer: Enhanced Transformer with Rotary Position Embedding【メモ】
イントロダクション
今回は『RoFormer: Enhanced Transformer with Rotary Position Embedding』という以下の論文を要約する。論文のpdfをClaude 3 Opusに渡して要約させた。
研究の目的と背景
<purpose>
本研究の目的は、Transformer言語モデルにおいて、相対位置情報を利用した新しい位置エンコーディング手法Rotary Position Embedding (RoPE)を提案し、性能を向上させることである。
Transformerは自己注意機構により文脈表現を捉えるが、位置情報を考慮しないという課題がある。そこで、相対位置情報を明示的に自己注意計算に組み込むことで、位置情報を効果的に活用し、性能向上を目指す。
提案手法RoPEは、回転行列により絶対位置をエンコードしつつ、自己注意の定式化に相対位置の依存性を組み込む。これにより、シーケンス長の柔軟性、相対距離の増加に伴うトークン間依存性の減衰、線形自己注意への適用可能性など、有用な特性を備えている。
RoPEをTransformerに組み込んだRoFormerを、長文テキスト分類のベンチマークで評価し、既存手法より一貫して優れた性能を示すことで、提案手法の有効性を実証する。理論的な説明も行い、実験結果の裏付けを行う。
言語モデルの性能向上は自然言語処理タスク全般に影響するため、本研究の意義は大きい。RoPEは簡潔かつ解釈可能な定式化により、効果的に位置情報を利用する新しいアプローチを提供するという点で独自性がある。
<background>
大規模事前学習済み言語モデル(PLM)は、自己注意機構を用いることでRNNやCNNを上回る性能を達成している。しかし、自己注意はデフォルトでは位置不変であり、トークンの順序情報を捉えられないという問題がある。この課題に対し、位置情報をモデルの学習過程に組み込む様々な手法が提案されてきた。絶対位置エンコーディングでは、事前に定義された関数(正弦波など)や学習可能なベクトルを文脈表現に加える方法が用いられる。一方、相対位置エンコーディングでは、注意機構そのものに相対位置情報を組み込む。例えばShaw et al. (2018)は、注意の重みに相対位置に基づくバイアス項を加える手法を提案した。しかし、既存手法の多くは位置情報を文脈表現に加算する形式を取っており、線形自己注意への適用が困難という問題がある。本研究のRoPEは、この課題を克服し、相対位置情報を回転行列の積として自己注意の計算に直接組み込むという新しいアプローチを提案する。
RoPEは、理論的な解釈が明確で、シーケンス長に依存せず、遠距離の相対位置では影響が減衰するなどの望ましい特性を備えている。Transformerの性能向上に向けた、簡潔かつ効果的な位置情報の利用法として位置づけられる。
使用した手法の概要
<methods>
本研究では、Transformer言語モデルにおいて位置情報を効果的に利用するため、新しい位置エンコーディング手法Rotary Position Embedding (RoPE)を提案している。RoPEの基本的な概念は、相対位置情報を回転行列の積により自己注意の計算に直接組み込むことである。2次元の場合、位置mのクエリqとキーkのRoPE後の表現は以下のようになる。
$${f_q(x_m, m) = (W_qx_m)e^{imθ}}$$
$${f_k(x_n, n) = (W_kx_n)e^{inθ}}$$
ここで、$${W_q, W_k}$$は重み行列、$${θ}$$は事前に設定される定数である。これは、アフィン変換後の単語埋め込みベクトルを、位置に基づく角度の整数倍だけ回転させることに相当する。
一般のd次元の場合(dは偶数)、d/2個の2次元部分空間に分割し、内積の線形性により結合することで、$${f_q, f_k}$$は以下のようになる。
$${f_q(x_m, m) = R^d_{Θ,m} W_qx_m}$$
$${f_k(x_n, n) = R^d_{Θ,n} W_kx_n}$$
ここで$${R^d_Θ,m}$$は、事前定義されたパラメータΘに基づいて構成される回転行列である。
RoPEはシーケンス長に依存せず、相対距離が大きいほど影響が減衰するなどの望ましい特性を備えている。また、提案手法は線形自己注意にも適用可能である。RoPEを自己注意計算に適用すると、以下のようになる。
$${q^⊺_mk_n = (R^d_{Θ,m}W_qx_m)^⊺(R^d_{Θ,n}W_kx_n) = x^⊺W_qR^d_{Θ,n-m}W_kx_n}$$
回転行列R^d_Θ,mは、直交行列であり、位置情報のエンコーディング時の安定性を保証する。
RoPEは理論的な解釈が明確で、相対位置情報を加法的ではなく乗法的に組み込むシンプルかつ効果的な手法である。提案手法の有効性は、機械翻訳、事前学習済み言語モデルの性能評価、GLUEベンチマーク等の下流タスクへの応用により実証されている。
<comparison>
RoPEと既存の位置エンコーディング手法を比較すると、以下のような特徴がある。絶対位置エンコーディングでは、正弦波関数や学習可能なベクトルを用いて位置情報を生成し、文脈表現に加算する。一方、相対位置エンコーディングでは、注意機構そのものに相対位置情報を組み込む。例えば、Shaw et al. (2018)は注意の重みに相対位置に基づくバイアス項を加える手法を提案している。
しかし、これらの手法は位置情報を文脈表現に加算する形式を取っており、線形自己注意への適用が困難という問題がある。RoPEはこの課題を克服し、相対位置情報を回転行列の積として自己注意の計算に直接組み込むという新しいアプローチを提供する。著者らは、理論的な解釈の明確さ、シーケンス長への非依存性、遠距離の相対位置での影響の減衰など、RoPEの望ましい特性を強調している。加えて、提案手法は線形自己注意にも適用可能であり、計算効率の面でも優れている。実験により、RoPEをTransformerに組み込んだRoFormerが、機械翻訳、言語モデルの事前学習、GLUEベンチマークなど、様々なタスクにおいて既存手法を上回る性能を示すことが確認された。
論文内の数式と手法の関連
以下論文内の数式を順に追っていき、RoPEの理論的背景を考えていく。
<equations>
本論文の式(1)から式(10)は、自己注意機構における位置情報の利用に関する既存の手法を表している。
式(1)は、位置情報を含む単語埋め込みからクエリ$q_m$、キー$k_n$、値$v_n$を生成する一般的な式である。
$$
q_m = f_q(x_m, m) \\
k_n = f_k(x_n, n) \\
v_n = f_v(x_n, n)
$$
ここで、$${f_q}$$, $${f_k}$$, $${f_v}$$は位置情報を組み込むための関数であり、$${x_m}$$, $${x_n}$$は単語埋め込み、$${m}$$, $${n}$$は位置を表す。この式は、位置情報を利用する自己注意機構の基礎となる。
式(2)は、式(1)で生成されたクエリ、キー、値を用いて、自己注意機構の出力を計算する式である。
$$
a_{m,n} = \frac{\exp(\frac{q_m^⊺k_n}{\sqrt{d}})}{\sum_{j=1}^N \exp(\frac{q_m^⊺k_j}{\sqrt{d}})} \\
o_m = \sum_{n=1}^N a_{m,n}v_n
$$
ここで、$${a_{m,n}}$$はアテンションの重みであり、$${q_m^⊺k_n}$$はクエリとキーの内積、$${d}$$は埋め込みの次元数である。$${o_m}$$は注意機構の出力であり、注意重みと値の加重和として計算される。
式(3)から式(10)は、位置情報を組み込むための関数$${f_q}$$, $${f_k}$$, $${f_v}$$の具体的な設計に関する式である。
式(3)は、絶対位置エンコーディングを表す式である。
$$
f_{t:t∈{\{q,k,v\}}}(x_i, i) := W_{t:t∈\{q,k,v\}}(x_i + p_i)
$$
ここで、$${p_i}$$は位置$${i}$$に対応する位置埋め込みベクトルであり、$${W_{t:t∈\{q,k,v\}}}$$は重み行列である。この式は、単語埋め込みに位置埋め込みを加算することで位置情報を組み込んでいる。
式(4)は、正弦波関数を用いた位置埋め込みの生成式である。
$$
p_{i,2t} = \sin(k/10000^{2t/d}) \\
p_{i,2t+1} = \cos(k/10000^{2t/d})
$$
ここで、$${p_{i,2t}}$$と$${p_{i,2t+1}}$$は位置埋め込みベクトル$${p_i}$$の偶数番目と奇数番目の要素であり、$${k}$$は位置、$${d}$$は埋め込みの次元数である。
式(5)から式(10)は、相対位置エンコーディングに関する式である。これらの式は、自己注意機構のクエリとキーの内積計算に相対位置情報を組み込む方法を表している。例えば、式(6)は、相対位置埋め込みを用いてクエリとキーの内積を分解する式である。
$$
q_m^⊺k_n = x_m^⊺W_q^⊺W_kx_n + x_m^⊺W_q^⊺W_kp_n + p_m^⊺W_q^⊺W_kx_n + p_m^⊺W_q^⊺W_kp_n
$$
ここで、$${p_m}$$と$${p_n}$$は位置$${m}$$と$${n}$$に対応する相対位置埋め込みである。
これらの式は、位置情報を利用する自己注意機構の様々な設計を表しており、RoPEが提案されるまでの関連研究の文脈を提供している。
式(11)から式(15)は、RoPEの中核となる数式であり、自己注意機構に相対位置情報を組み込む方法を定式化している。
以下の式(11)は、RoPEの基本的な考え方を表す式である。
$$
\langle f_q(\mathbf{x}_m, m), f_k(\mathbf{x}_n, n)\rangle = g(\mathbf{x}_m, \mathbf{x}_n, m-n)
$$
ここで、$${f_q}$$と$${f_k}$$は、それぞれクエリとキーに位置情報を組み込む関数であり、$${g}$$は単語の埋め込み$${x_m}$$,$${x_n}$$と相対位置$${m-n}$$のみに依存する関数である。この式は、クエリとキーの内積が相対位置のみに依存することを表しており、RoPEの目的を明確に示している。
以下の式(12)は、RoPEの2次元での具体的な実装を表す式である。
$$
f_q(\mathbf{x}_m, m) = (\mathbf{W}_q\mathbf{x}_m)e^{imθ} \\
f_k(\mathbf{x}_n, n) = (\mathbf{W}_k\mathbf{x}_n)e^{inθ} \\
g(\mathbf{x}_m, \mathbf{x}_n, m-n) = \text{Re}[(\mathbf{W}_q\mathbf{x}_m)(\mathbf{W}_k\mathbf{x}_n)^*e^{i(m-n)θ}]
$$
ここで、$${\mathbf{W}_q}$$と$${\mathbf{W}_k}$$は重み行列、θは事前に設定される定数、$${\text{Re}[\cdot]}$$は複素数の実部を表す。この式は、単語埋め込み$${x_m}$$と$${x_n}$$に回転行列$${e^{imθ}}$$と$${e^{inθ}}$$をかけることで位置情報を組み込み、その内積の実部を取ることで相対位置のみに依存する値を得ることを示している。
以下の式(13)は、式(12)の回転行列を明示的に表現した式である。
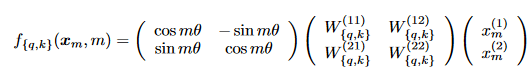
ここで、$${x_m^{(1)}}$$と$${x_m^{(2)}}$$は、単語埋め込み$${x_m}$$の2次元座標表現である。この式は、RoPEが単語埋め込みを回転行列によって変換することで位置情報を組み込むことを明示している。
以下の式(14)は、RoPEをd次元に一般化した式である。
$$
f_{(q,k)}(\mathbf{x}_m, m) = \mathbf{R}^d_{Θ,m}\mathbf{W}_{\{q,k\}}\mathbf{x}_m
$$
ここで、$${\mathbf{R}^d_{Θ,m}}$$は以下の式(15)で定義される回転行列である。

この式は、RoPEがd次元空間をd/2個の2次元部分空間に分割し、各部分空間で2次元の場合と同様に回転操作を適用することを示している。
ここで、
$${{Θ=(θ_i=10000^{-2(i-1)/d})}, i∈[1,2,\ldots,d/2])}$$は事前に定義されたパラメータである。
これらの式は、RoPEの基本的なアイデアである相対位置情報の導入と、その自己注意機構への組み込み方法を数学的に定式化したものであり、RoPEの実装と動作の基礎となっている。
以下の式(16)は、RoPEを自己注意機構のクエリ・キー内積計算に適用した式である。
$$
\mathbf{q}_m^⊺\mathbf{k}_n = (\mathbf{R}^d_{Θ,m}\mathbf{W}_q\mathbf{x}_m)^⊺(\mathbf{R}^d_{Θ,n}\mathbf{W}_k\mathbf{x}_n) = \mathbf{x}^⊺\mathbf{W}q\mathbf{R}^d_{Θ,n-m}\mathbf{W}_k\mathbf{x}_n
$$
ここで、$${\mathbf{R}^d_{Θ,n-m} = (\mathbf{R}^d_{Θ,m})^⊺\mathbf{R}^d_{Θ,n}}$$である。この式は、RoPEによって位置情報がエンコードされたクエリとキーの内積計算を表している。回転行列$${\mathbf{R}^d_{Θ,m}}$$は直交行列であるため、位置情報のエンコーディング時の安定性が保証される。
以下の式(17)は、自己注意機構の一般的な定式化である。
$$
\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V})_m = \frac{\sum_{n=1}^N \text{sim}(\mathbf{q}_m, \mathbf{k}_n)\mathbf{v}_n}{\sum_{n=1}^N \text{sim}(\mathbf{q}_m, \mathbf{k}_n)}
$$
ここで、$${\text{sim}(q_m, k_n)}$$はクエリ$${q_m}$$とキー$${k_n}$$の類似度を表す関数である。元の自己注意機構では、$${\text{sim}(q_m, k_n) = \exp(q_m^⊺k_n/\sqrt{d})}$$が使用される。
以下の式(18)は、線形注意機構の定式化である。
$$
\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V})_m = \frac{\sum_{n=1}^N ϕ(\mathbf{q}_m)^⊺φ(\mathbf{k}_n)\mathbf{v}_n}{\sum_{n=1}^N ϕ(\mathbf{q}_m)^⊺φ(\mathbf{k}_n)}
$$
ここで、$φ(・)$と$ψ(・)$は非負の関数である。線形注意機構は、自己注意機構の計算量を$O(N^2)$から$O(N)$に削減することを目的としている。
以下の式(19)は、RoPEを線形注意機構に適用した式である。
$$
\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V})m = \frac{\sum_{n=1}^N (\mathbf{R}^d_{Θ,m}ϕ(\mathbf{q}_m))^⊺(\mathbf{R}^d_{Θ,n}φ(\mathbf{k}_n))\mathbf{v}_n}{\sum_{n=1}^N ϕ(\mathbf{q}_m)^⊺φ(\mathbf{k}_n)}
$$
ここで、分母は位置情報の影響を受けないように変更されていない。この式は、RoPEが線形注意機構にも適用可能であり、位置情報を効果的に取り入れることができることを示している。
これらの式は、RoPEが自己注意機構および線形注意機構において位置情報をどのように組み込むかを明確に表現しており、RoPEの実装と動作に直接寄与している。
式(20)から式(27)は、RoPEの2次元の場合の導出過程で用いられる数式である。これらの式は、RoPEの理論的な基盤を与えるものであり、位置情報を単語埋め込みの回転として表現するというアイデアを明確にしている。
以下の式(20)は、位置$${m}$$と$${n}$$におけるクエリ$${q_m}$$とキー$${k_n}$$の位置情報を含む表現を定義している。
$$
\mathbf{q}_m = f_q(\mathbf{x}_q, m) \\
\mathbf{k}_n = f_k(\mathbf{x}_k, n)
$$
ここで、$${f_q}$$と$${f_k}$$は位置情報を組み込む関数、$${\mathbf{x}_q}$$と$${\mathbf{x}_k}$$はクエリとキーに対応する単語埋め込みである。
以下の式(21)は、式(20)で定義された$${\mathbf{q}_m}$$と$${\mathbf{k}_n}$$の内積が、単語埋め込み$${\mathbf{x}_m}$$、$${\mathbf{x}_n}$$と相対位置$${n-m}$$のみに依存する関数$${g}$$で表されることを仮定している。
$$
\mathbf{q}_m^⊺\mathbf{k}_n = ⟨f_q(\mathbf{x}_m, m), f_k(\mathbf{x}_n, n)⟩ = g(\mathbf{x}_m, \mathbf{x}_n, n-m)
$$
以下の式(22)は、位置情報が含まれない場合の初期条件を定義している。
$$
\mathbf{q} = f_q(\mathbf{x}_q, 0) \\
\mathbf{k} = f_k(\mathbf{x}_k, 0)
$$
式(23)は、式(20)と式(21)の関数$${f_q}$$、$${f_k}$$、$${g}$$を極座標形式で表現している。
$$
f_q(\mathbf{x}_q, m) = R_q(\mathbf{x}_q, m)e^{iΘ_q(\mathbf{x}_q,m)}\\
f_k(\mathbf{x}_k, n) = R_k(\mathbf{x}_k, n)e^{iΘ_k(\mathbf{x}_k,n)}\\
g(\mathbf{x}_q, \mathbf{x}_k, n-m) = R_g(\mathbf{x}_q, \mathbf{x}_k, n-m)e^{iΘ_g(\mathbf{x}_q,\mathbf{x}_k,n-m)}
$$
ここで、$${R_f}$$、$${R_g}$$と$${Θ_f}$$、$${Θ_g}$$は、それぞれ$${f_{(q,k)}}$$と$${g}$$の動径成分と角度成分である。
式(24)から式(26)は、式(23)を式(21)と式(22)に代入することで得られる関係式であり、$${f_q}$$、$${f_k}$$、$${g}$$の動径成分と角度成分に対する制約を表している。
式(24)
$$
R_q(\mathbf{x}_q, m)R_k(\mathbf{x}_k, n) = R_g(\mathbf{x}_q, \mathbf{x}_k, n-m)\\
Θ_k(\mathbf{x}_k, n) - Θ_q(\mathbf{x}_q, m) = Θ_g(\mathbf{x}_q, \mathbf{x}_k, n-m)
$$
式(25)
$$
\mathbf{q} = ‖\mathbf{q}‖e^{iθ_q} = R_q(\mathbf{x}_q, 0)e^{iΘ_q(\mathbf{x}_q,0)} \\
\mathbf{k} = ‖\mathbf{k}‖e^{iθ_k} = R_k(\mathbf{x}_k, 0)e^{iΘ_k(\mathbf{x}_k,0)}
$$
式(26)
$$
R_q(\mathbf{x}_q, m)R_k(\mathbf{x}_k, m) = R_g(\mathbf{x}_q, \mathbf{x}_k, 0) = R_q(\mathbf{x}_q, 0)R_k(\mathbf{x}_k, 0) = ‖\mathbf{q}‖‖\mathbf{k}‖ \\
Θ_k(\mathbf{x}_k, m) - Θ_q(\mathbf{x}_q, m) = Θ_g(\mathbf{x}_q, \mathbf{x}_k, 0) = Θ_k(\mathbf{x}_k, 0) - Θ_q(\mathbf{x}_q, 0) = θ_k - θ_q
$$
以下の式(27)は、式(24)から式(26)を満たす$${R_f}$$の解の一つである。
$$
R_q(\mathbf{x}_q, m) = R_q(\mathbf{x}_q, 0) = ‖\mathbf{q}‖ \\
R_k(\mathbf{x}_k, n) = R_k(\mathbf{x}_k, 0) = ‖\mathbf{k}‖ \\
R_g(\mathbf{x}_q, \mathbf{x}_k, n-m) = R_g(\mathbf{x}_q, \mathbf{x}_k, 0) = ‖\mathbf{q}‖‖\mathbf{k}‖
$$
式(28)は、式(24)から導出された角度関数$${Θ_f}$$の表現である。
$$
Θ_f(x_{(q,k)}, m) = φ(m) + θ_{(q,k)}
$$
ここで、$${φ(m)}$$は位置$${m}$$のみに依存する関数、$${θ_{(q,k)}}$$は単語埋め込み$${x_{(q,k)}}$$に依存する定数である。
以下の式(29)は、式(28)にn=m+1を代入して、式(24)を考えることで得られる関係式である。
$$
φ(m+1) - φ(m) = Θ_g(\mathbf{x}_q, \mathbf{x}_k, 1) + θ_q - θ_k
$$
これは、$${φ(m)}$$が位置$${m}$$に関する等差数列であることを示している。
式(30)は、式(29)の関係式を満たす$${φ(m)}$$の一般形である。
$$
φ(m) = mθ + γ
$$
ここで、$${θ}$$と$${γ}$$は定数であり、$${θ}$$は0でない。
式(31)は、式(27)から式(30)を用いて、$${f_q}$$と$${f_k}$$の解を表している。
$$
f_q(\mathbf{x}_q, m)=‖\mathbf{q}‖e^{iθ_q+mθ+γ} = \mathbf{q}e^{i(mθ+γ)} \\
f_k(\mathbf{x}_k, n)=‖\mathbf{k}‖e^{iθ_k+nθ+γ} = \mathbf{k}e^{i(nθ+γ)}
$$
式(32)は、式(22)の制約を適用せず、$${f_q(x_m, 0)}$$と$${f_k(x_n, 0)}$$を定義している。
$$
\mathbf{q} = f_q(\mathbf{x}_m, 0) = \mathbf{W}_q\mathbf{x}_n \\
\mathbf{k} = f_k(\mathbf{x}_n, 0) = \mathbf{W}_k\mathbf{x}_n
$$
式(33)は、式(31)と式(32)を組み合わせ、$${γ=0}$$とすることで得られる$${f_q}$$と$${f_k}$$の最終的な解である。
$$
f_q(\mathbf{x}_m, m) = (\mathbf{W}_q\mathbf{x}_m)e^{imθ} \\
f_k(\mathbf{x}_n, n) = (\mathbf{W}_k\mathbf{x}_n)e^{inθ}
$$
この式は、位置情報を単語埋め込みベクトルに回転行列を乗じることで組み込んでいることを明確に示しています。$${e^{imθ}}$$と$${e^{inθ}}$$は、それぞれ位置$${m}$$と$${n}$$に対応する回転行列です。
式(34)は、式(15)の回転行列$${\mathbf{R}^d_{Θ,m}}$$の計算を効率化するための公式である。

ここで、$${⊗}$$はアダマール積(要素ごとの積)を表す。この式は、$${\mathbf{R}^d_{Θ,m}}$$のスパース性を利用することで、効率的な計算を可能にしている。
式(35)から式(37)は、RoPEの理論的説明において、長距離依存性の減衰に関する性質を導出するために用いられている。
式(35)は、複素数表現を用いて、RoPEを適用した後のクエリ$${q}$$とキー$${k}$$の内積を表している。
$$
(\mathbf{R}^d_{Θ,m}\mathbf{W}_q\mathbf{x}_m)^⊺(\mathbf{R}^d_{Θ,n}\mathbf{W}_k\mathbf{x}_n) = \text{Re}\left[\sum_{i=0}^{d/2-1}\mathbf{q}_{[2i:2i+1]}\mathbf{k}^*_{[2i:2i+1]}e^{i(m-n)θ_i}\right]
$$
ここで、$${q_{[2i:2i+1]}}$$と$${k_{[2i:2i+1]}}$$は、それぞれ$${q}$$と$${k}$$の$${2i}$$番目と$${2i+1}$$番目の要素を表す。この式は、$${d}$$次元ベクトルを$${d/2}$$個の2次元ベクトルに分解し、各2次元ベクトルについて複素数の積を計算することを示している。
式(36)は、式(35)の和の計算にAbel変換を適用することで得られる式である。
$$
\sum_{i=0}^{d/2-1}\mathbf{q}_{[2i:2i+1]}\mathbf{k}^*_{[2i:2i+1]}e^{i(m-n)θ_i} = -\sum_{i=0}^{d/2-1}S_{i+1}(h_{i+1} - h_i)
$$
ここで、$${h_i = q_{[2i:2i+1]}k^*_{[2i:2i+1]}}$$、$${S_j = \sum_{i=0}^{j-1}e^{i(m-n)θ_i}}$$、$${h_{d/2} = 0}$$、$${S_0 = 0}$$である。この式は、部分和$${S_i}$$と隣接する$${h_i}$$の差を用いて、式(35)内の要素を変形している。
式(37)は、式(36)に絶対値の不等式を適用することで得られる上界である。
$${\left|\sum_{i=0}^{d/2-1}q_{[2i:2i+1]}k^*_{[2i:2i+1]}e^{i(m-n)θ_i}\right| \leq \left(\max_i|h_{i+1} - h_i|\right)\sum_{i=0}^{d/2-1}|S_{i+1}|}$$
この式は、元の和の絶対値が、隣接する$${h_i}$$の差の最大値と部分和$${S_i}$$の絶対値の和の積で抑えられることを示している。
式(35)から式(37)は、RoPEの長距離依存性の減衰に関する性質を理論的に説明するために用いられている。この性質は、RoPEが自然言語処理タスクにおいて効果的に位置情報を利用できることの根拠の一つとなっている。
式(37)の上界は、部分和$${S_i}$$の絶対値の和$${\sum_{i=0}^{d/2-1}|S_{i+1}|}$$に依存している。論文では、パラメータ$${θ_i}$$を$${10000^{-2i/d}}$$に設定することで、$${\frac{1}{d/2}\sum_{i=1}^{d/2}|S_i|}$$が相対距離$${m-n}$$が大きくなるにつれて減衰することが示されている。この減衰の速さは、パラメータ$${θ_i}$$の設定に直接的に依存している。
式(37)は、RoPEを適用した後のクエリ$${q}$$とキー$${k}$$の内積の絶対値の上界を与えています。ここで、$${S_j}$$は以下のように定義されています。 $${S_j = \sum_{i=0}^{j-1}e^{i(m-n)θ_i}}$$
$${S_j}$$を展開すると、以下のようになります。 $${S_j = 1 + e^{i(m-n)θ_1} + e^{i(m-n)θ_2} + \cdots + e^{i(m-n)θ_{j-1}}}$$
$${S_j}$$は、相対位置$${m-n}$$と角度$${θ_i}$$に依存する$${j}$$個の複素数の和です。$${θ_i}$$は、以下のように設定されています。 $${θ_i = 10000^{-2i/d}}$$
この設定により、$${i}$$が大きくなるにつれて$${θ_i}$$が急速に小さくなります。その結果、$${e^{i(m-n)θ_i}}$$の値は、$${i}$$が大きくなるにつれて1に近づきます。
式(37)の上界は、$${\sum_{i=0}^{d/2-1}|S_{i+1}|}$$に依存しています。$${|S_{i+1}|}$$は、$${S_{i+1}}$$の絶対値を表します。相対位置$${m-n}$$が大きくなるにつれて、$${e^{i(m-n)θ_i}}$$の値が1に近づくため、$${ S_{i+1}}$$の値は$${i+1}$$に近づきます。したがって、$${ \sum_{i=0}^{d/2-1}|S_{i+1}|}$$の値は、相対位置$${m-n}$$が大きくなるにつれて、$${\sum_{i=0}^{d/2-1}(i+1)}$$に近づきます。
しかし、$${θ_i}$$が$${ 10000^{-2i/d}}$$に設定されているため、$${i}$$が大きくなるにつれて$${e^{i(m-n)θ_i}}$$の値は急速に1に近づきます。その結果、$${\sum_{i=0}^{d/2-1}|S_{i+1}|}$$の値は、相対位置$${m-n}$$が大きくなるにつれて、$${\sum_{i=0}^{d/2-1}(i+1)}$$よりも急速に収束します。
θが持つ理論的性質
RoPEにおいて、パラメータ$${θ_i}$$は回転行列$${R^d_{Θ,m}}$$の角度成分を決定する重要な役割を果たしている。論文では、$${θ_i}$$を以下のように設定している。 $${θ_i = 10000^{-2(i-1)/d}, \quad i∈[1,2,\ldots,d/2]}$$ ここで、$${d}$$はベクトルの次元数である。
この設定は、RoPEが位置情報を効率的かつ効果的にエンコードすることを可能にしている。LLMへの入力トークン数が大きい場合、RoPEではベクトルの次元数$${d}$$を大きくする必要がある。これは、より長い文脈を扱うために、より多くの位置情報を表現する必要があるためである。$${d}$$が大きくなると、$${θ_i}$$の減衰がより緩やかになる。これは、式(37)の部分和$${S_i}$$の減衰がより緩やかになることを意味する。
$${d}$$が大きくなると、$${θ_i}$$の減衰が緩やかになるため、$${\frac{1}{d/2}\sum_{i=1}^{d/2}|S_i|}$$の減衰も緩やかになる。これは、長距離の依存関係がより考慮されるようになることを意味する。入力トークン数が大きい場合、RoPEは長距離の文脈情報をより多く取り入れることができるようになる。
以上のように、$${θ_i}$$の設定は、RoPEの位置情報のエンコードに重要な役割を果たしている。入力トークン数が大きい場合、$${d}$$を大きくすることで、長距離の文脈情報をより多く取り入れることができるようになる。
$${θ_i}$$内の定数(=10000)を増加させると、$${θ_i}$$の減衰速度が速くなり、その結果、長距離の文脈の考慮度合いが減少することになります。
$${θ_i}$$は以下のように設定されています。 $${θ_i = 10000^{-2(i-1)/d}, \quad i∈[1,2,\ldots,d/2]}$$
ここで、定数項である$${10000}$$を増加させると、$${θ_i}$$の値がより急速に減衰することになります。例えば、定数項を$${100000}$$に変更すると、以下のようになります。 $${θ_i = 100000^{-2(i-1)/d}, \quad i∈[1,2,\ldots,d/2]}$$
この場合、$${i}$$が小さい値に対しても、$${θ_i}$$の値が非常に小さくなります。これは、低次元の回転成分が位置情報のエンコードにおいてより重要になることを意味しています。
その結果、式(37)の部分和$${S_i}$$の減衰もより急速になります。$${\frac{1}{d/2}\sum_{i=1}^{d/2}|S_i|}$$の値が相対距離$${m-n}$$の増加に伴ってより急速に減衰することになります。これは、長距離の依存関係がより強く抑制され、短距離の依存関係がより重視されるようになることを意味しています。
逆に、定数項を減少させると、$${θ_i}$$の減衰速度が遅くなり、長距離の文脈の考慮度合いが増加することになります。
したがって、$${θ_i}$$内の定数項を調整することで、RoPEにおける長距離の文脈の考慮度合いを制御することができます。定数項を増加させると長距離の文脈の考慮度合いが減少し、定数項を減少させると長距離の文脈の考慮度合いが増加します。
得られた主な結果
<main_results>
本研究では、Transformer言語モデルにおける新しい位置エンコーディング手法であるRotary Position Embedding (RoPE)を提案し、その有効性を実証した。
RoPEは、相対位置情報を回転行列により自己注意機構に直接組み込むことで、位置情報を効果的に利用することを可能にする。RoPEを組み込んだRoFormerを様々なタスクで評価した結果、以下のような主要な結果が得られた。
機械翻訳タスク(WMT 2014 English-to-German)において、RoFormerはベースラインのTransformerを上回るBLEUスコア(27.5 vs 27.3)を達成した。
言語モデルの事前学習において、RoFormerはBERTと比較して、MLM損失の収束が速く、より低い損失値を達成した。
GLUEベンチマークの下流タスクにおいて、RoFormerはBERTを3つのデータセット(MRPC、QQP、STS-B)で大幅に上回った。
PerFormerにRoPEを組み込むことで、RoPE無しの場合と比べて、言語モデルの学習が速くなり、低い損失値を達成することが示された。
中国語のデータセットにおいて、RoFormerはWoBERTやNEZHAなどの既存の事前学習モデルを上回る性能を示した。特に、長文テキストのマッチングタスク(CAIL2019-SCM)では、最大入力長を1024に設定したRoFormerが、512の場合と比べて1.5%の絶対的な改善を達成した。
これらの結果は、RoPEがTransformerベースのモデルの性能を向上させ、様々なタスクで有効であることを示している。特に、RoPEは長距離の依存関係を適切に扱うことができるため、長文テキストを扱うタスクにおいて優れた性能を発揮すると考えられる。
<details>
1.機械翻訳タスクにおけるRoFormerの優位性は、BLEUスコアの絶対的な改善幅は小さいものの(0.2ポイント)、一貫した改善が見られたことが重要である。ただし、この結果はWMT 2014 English-to-Germanデータセットに限定されるため、他の言語ペアや翻訳タスクでの一般化可能性は検証が必要である。
2.事前学習タスクにおけるRoFormerの収束速度と最終的な損失値は、BERTと比較して優れていた。これは、RoPEが事前学習段階から位置情報を効果的に利用できることを示唆している。ただし、事前学習データセットはBookCorpusとWikipediaに限定されているため、他のドメインでの有効性は検証が必要である。
3.GLUEベンチマークでは、RoFormerがBERTを上回ったのは3つのデータセット(MRPC、QQP、STS-B)のみであり、他のデータセットではBERTと同等か下回る結果となった。
4.PerFormerへのRoPEの組み込みは、計算効率と性能の両面で有効であることが示された。ただし、本研究ではPerFormerの特定の設定(12層、768次元、12ヘッド)のみが検証されているため、他の設定での有効性は検証が必要である。
5.中国語データセットにおけるRoFormerの優位性は、特に長文テキストのマッチングタスクで顕著であった。これは、RoPEが長距離の依存関係を適切に扱うことができることを示唆している。
