
食塩水の濃度と天秤
てんびん図,面積図という言葉をご存知だろうか.私からすると,これは,本質的には「はじき」という単位量あたりの計算の鬼子よりも酷いものだ.事は,私が子供のために本屋で思いついて,算数の問題集を買ったことに起因する.そこで下のような問題に出くわした.
濃度4%の食塩水100gに,濃度3%の食塩水をいくらか加えて,よく混ぜたところ,濃度3.2%の食塩水が得られた.濃度3%の食塩水をいくら加えたか?
よくある,食塩水の濃度に関わる問題である.これは,初等的な代数と,濃度の理解を問う問題である.普通に解答するのであれば,題意の通りに立式すれば良い.濃度3%の食塩水が$${x}$$gであるとすると,混ぜ合わせる前後の食塩の量が同じであることから,以下の式が成り立つ.
$$
0.04 \times 100 + 0.03 \times x=0.032 \times (100 + x)
$$
当然,この式を展開し,
$$
0.04 \times 100 + 0.03 \times x=0.032 \times (100 + x) \\
4 \times 100 + 3x=3.2 \times (100 + x) \\
400 + 3x=320 + 3.2x \\
0.2x = 80 \\
x = 400
$$
となるため,解答の結論として,$${400}$$gが得られる.何のことはない算数の問題である.しかし,小学生がこれを解こうとすると,初等代数を知らないため,式展開ができない.世間に広く知られる「習ってないことを解答に使ってはならない」という迷信のため,世の解説文は上のような回答を提示しない.しかし,この迷信もさることながら,初等代数を小学生に伝えるのも割と時間がかかるもので,これはこれで大変である.私などは,「そもそも代数を知らない小学生にこういう問題をやらせるな」という意見なのだが,算数の問題集などには,このような問題が当然の如く掲載されており・・・・とりあえず,子供に教えるにもなかなか大変なのである.
謎の解答例
そこで,問題集の解答例や解説文を読んでみると,衝撃の解答例が載っていたである.これが,本題の「てんびん図」なのである.この解説に基づき,上の自作の例題を解答すると,
解答例
てんびん図に問題を表すと下図のようになる.
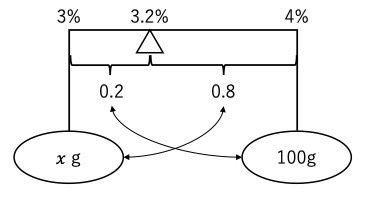
食塩水の重の差の比は,濃度の差の逆比になるから,
$$
100 : x = (3.2 - 3) : (4 - 3.2) \\
100 : x = 0.2 : 0.8 \\
100 : x = 1 : 4 \\
x = 400
$$
ゆえに,正解は,400gである.
え・・・・?
天秤・・・・?食塩水ですよ・・・?天秤・・・・?んで,なんだかんだ$${x}$$使ってもうてるし・・・なにこれ.全然理解できないんですが・・・.逆比?濃度比・・・?へ??
問題集の解説もおざなりで,天下りで,てんびん図で解けと書いてある.意味がわからない.ネットで調べてみても,的を射た説明はなく,面積図なるものも存在を知り,混乱する.しかし,この面積図を理解することで,私は,難解なてんびん図の意味を理解することができた.まず,面積図を説明しよう.
面積図
面積図も,塾のサイトなどで当たり前の定義のように使われているが・・・.そんなものは当然,中学受験用語であり,数学的に知られたものではない.この面積図の考え方自体は一見よいものに見えるが,本質は食塩水の濃度を無関係である.先に結論を言うと,変数整理を図でやってしまうための詭弁に近く,代数計算を知っていれば,こんなパズルのような解法を弄する必要はない.
面積図では,長方形の横方向の長さを食塩水の質量,縦方向の長さを濃度として定義する.すると,長方形の面積が食塩水の塩の質量ということになる.下図は,面積図を,図示しやすいように縦横のスケールを調整したものである.

図2から,混ぜ合わせた食塩水は,水色+青色の長方形(4%の食塩水)の面積と,緑色の長方形(3%の食塩水)の面積に相当する食塩を含むことがわかる.一方,混ぜ合わせて得られる食塩水を図で考えると,高さ(つまり濃度)が3.2%で,幅(つまり食塩水の質量)が$${100 + x}$$gになるので,その食塩の量は,赤枠で囲んだ長方形になる.足し合わせる前後で食塩の総量は変化しないため,図2の水色の長方形と,赤枠の白い部分の長方形の面積は一致しなければならない.
このことから,左辺を水色の長方形,右辺を赤枠の白い部分の長方形の面積として式を立てると,
$$
(0.04 - 0.032) \times 100 = (0.032 - 0.03) \times x \\
$$
が成り立つ.この式は,最初の代数方程式の最後の形に他ならず,
$$
0.008 \times 100 = 0.002 \times x \\
400 = x
$$
という結果が得られる.面積図は,代数方程式の計算を図形で行なったものと解釈できる.つまるところ,この面倒な思考は,代数方程式による計算を回避するためのものであり,食塩水の濃度を理解することと何の関係もない.代数方程式の計算を意味することを解釈する・・・という意味では,おもしろいと考えることもできるが,小学生に盲目的に教えるのは,論外である.この面積図の考え方を説明せずに,問題の解法として紹介しているサイトもネット上には散見され,数学を何でもかんでも公式にあてはめて解くものだという先入観の原因になっていないかと危惧するところである.
てんびん図の正体
話は戻って,てんびん図である.読者の方は,もうお気づきかと思うが,てんびん図は,この面積図の基本的な解釈をとっぱらい,最後の結論に行くための手続きなのである.上で説明した面積の一致を示す式は,以下のように展開できる.
$$
(0.04 - 0.032) \times 100 = (0.032 - 0.03) \times x \\
(0.04 - 0.032) / x = (0.032 - 0.03) / 100 \\
0.008 : x = 0.002 : 100
$$
これは,まさにてんびん図の言うところの濃度の比の逆比になっている.この面積図の結論,代数方程式の最終形態に一発で飛ぶためのアルゴリズムがてんびん図ということになる.うーむ・・・・.これに当てはめる能力が一体,何の役に立つのか私にはさっぱりわからない.当てはめて解いてる子供たちのどれくらいが,果たしててんびん図アルゴリズムの意味を理解しているのだろうか.どこかの中学校でてんびん図アルゴリズムの意味を説明される問題を出して欲しいものだ.この図への帰着を理解させるのではあれば,てんびん図も面積図もそこまで悪い図で話ではない.これは,問題を解釈し,抽象的な代数や幾何に帰着させることは,初等的な数学,算数の中核を成すところであると私は考えるからだ.
まとめ
てんびん図は,食塩水の代数方程式の解法を迂回するためのものであり,全体の解釈さえ,飛び越し,さっさと結果を得るためのアルゴリズムであることがわかった.このアルゴリズムにパラメータを当てはめて,食塩水の濃度を計算しろと解答例を示す問題集にも閉口するが,こんな奇怪なアルゴリズムでしか解けないような問題を出す方も出す方である.もはや,算数が簡単すぎてこのような奇怪な手法を弄するような問題を出さないと算数のテストの点数が飽和してしまうのが原因なのだろうが,そうなら,代数方程式で解くようにして解説してしまった方が早いとも言える.
小学校で教えられていないことを出題するのは不平等だとか,そのような解答を認めないという教師や塾講師のせいで,このような歪んだ状態になっていると私は考える.とかく,世の中には「習っていない手法で解答してはならない」という呪いが蔓延しているように私には感じられてならない.
神戸市の私立・灘中学校の大西衡教頭は「方程式も正しければマル。正しいものをバツにする理由がない。児童が勉強を先に進めてはダメな理由もありません」と話します。
日本のトップの中学校の教頭がこのような話をしてくれるのはうれしいことではあるが,市中には,アルゴリズムあてはめ問題集が跋扈しているのも事実である.果たして,中学受験数学に意味はあるのだろうか・・・・.
この記事が気に入ったらサポートをしてみませんか?
