２０２２年九大理系数学［３］その１

今回から３回に分けて、２０２２年九大理系数学［３］を解説します。
問題はこちら

今年の５題のセットの中で、最も難しい問題でした。一つ一つの要素を丁寧に分析、見極めて論証の方向性を整えることが求められる問題で、ハイレベルの良問だったと思います。

ここ数年、徐々に難化傾向となっていた九大理系数学の新たな到達点とも言える問題かなと思います。

では、今回は（１）を見ていきましょう。
問題は、（ｎ^２＋１）/２　と、（ｎ^２ー１）/２が整数でかつお互いに素であることを示すことを求めています。

なので、論証の方向性として、これを二つに切り分けましょう。
まず、（ｎ^２＋１）/２　と、（ｎ^２ー１）/２が整数であることを示します。
①の右辺は、ｍ^２の値に関わらず奇数と言えるので、左辺のｎ^４は奇数であり、当然ｎ^２、ｎも奇数と言えます。
よって、ｎ^２ー１，ｎ^２＋１は偶数と言えるので、
（ｎ^２＋１）/２　と、（ｎ^２ー１）/２は整数と言えます。

次に、（ｎ^２＋１）/２　と、（ｎ^２ー１）/２がお互いに素であることを示します。
一般にお互いに素であることを示す場合、最大公約数ｇを設定し、ｇ＝１を示す流れです。
ｎ^２を消していくと、方向性が見えてきます。

最後は

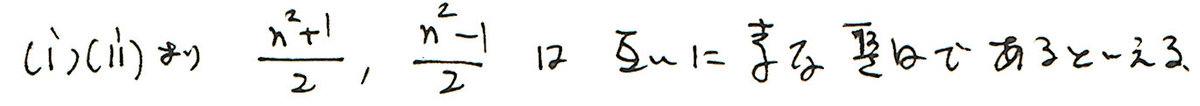
と結論づけることが出来ます。

この（ｎ^２＋１）/２　と、（ｎ^２ー１）/２がお互いに素であることは、（２）にじわりと効いてきます。

（２）まで手がつけられれば、合格安全圏に入ったと思うので、（２）が勝負所です。次回は（２）について解説します。