【解説】統計検定 2019年準1級 問2（幾何分布）

問題本文

問題本文は公式サイト又は公式問題集を参照してください。

問題解説（1）

問題要約

3枚のカード[x1, x2, x3]がどれも等しい確率で手に入る。
この時、全てのカードを買い揃える為に必要な購入回数の期待値を答えよ。

【ヒント】
幾何分布の期待値は以下の式を用いて良い。

幾何分布の期待値

回答

期待値: 5.5

解説

本問では幾何分布に関する基礎的な知識が問われています。
問題文中に期待値の求め方が示されている為、未所持のカードを入手する確率が分かれば以下の通り答えが求まります。

未所持のn枚目のカードを入手する確率

3枚のカードを揃える為に必要な購入回数の期待値

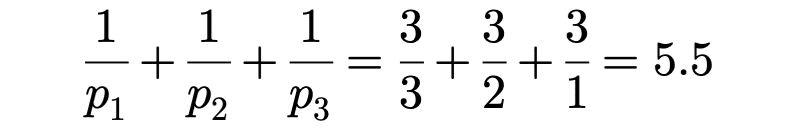
問題解説（2）

問題要約

4枚のカード[x1, x2, x3, x4]がどれも等しい確率で手に入る。
この時、以下に示すA, Bの方法で全てのカードを買い揃えた時、必要な購入回数の期待値の差を答えよ。

A: [x1, x2, x3]のカードを買い揃えた後、新たに発売されたx4を揃える
B: x4が発売された後に[x1, x2, x3, x4]のカードを揃える

回答

7/6

解説

(1)の問題が解けた方であれば、難なく解ける問題になっています。

A, Bで未所持のn枚目のカードを取得する確率

A, Bでカードを全て揃える為に必要な購入回数の期待値

A, Bでカードを全て揃える為に必要な購入回数の期待値の差

補足

本問では『成功までの回数を表したモデル』として幾何分布を扱いました。
しかし、負の二項分布に併せて『成功までに失敗した回数を表したモデル』として扱われることもあります。

文脈からどちらを指しているのか判断できるよう注意してください。