見出し画像

数式は触ってみないと何も分からない

shi3z

数式って不便すぎないか?

いやわからん。
俺は数学苦手だから。

でも例えば、プログラミング言語は、現代普通に使われるものだけ挙げても、C#、JavaScript、Ruby、Python、PHP、Java、Swiftとまあ軽く7種類くらい。C系で言えば、C、C++もあるし、C++もバージョンによってはほとんど別物になったりする。プログラミング言語ではない人工言語としても、HTML、SQL、VHDL・・・アセンブリ言語などがあり、使う人は少ないが恩恵に預かってる人が多い言語で言うとLISPやHaskellなんてのもある。

しかもこれらのプログラミング言語は、すべて「同じアルゴリズム」を記述することが可能なのだ。

「同じことを説明するのに複数の方法(言語)がある」と言うことが一体何の意味があるのか、プログラマー以外の人にはわかりにくいだろうが、プログラマーにとっては大問題である。

それぞれのプログラミング言語は、「この処理はこう書きたい」という言語設計者の欲求から設計されている。今簡単に「言語」と言ったけれども、実は「言語」と言うのは非常に低いレイヤーの話で、「この処理をこう書きたい」は、フレームワークでも表現される。

「こう書きたい」は「ここは書きたくない」の裏返しでもあり、「ここは書きたくない」部分をフレームワークが隠蔽する。面白いのは、フレームワーク開発者は設計上「書きたくない」部分を書くことに集中するのである。

すると、たとえ言語が同じでも、使うフレームワークが違えば全く異なる世界に突入すると言うことになる。

これに比べると、数式は表現力が弱い。
同じことを複数の表現で書けなくはないが、何となく全体的な互換性を考えているような気がする。そこが数式の良さでもあるが欠点でもあると思う。

例えば明らかに同じことを違う書き方で書くといえば、微分の書き方でいろんな種類がある。

行列の掛け算も、馴染みの方法以外に、量子力学ではブラ-ケット記法と言う奇妙な書き方ができる。

それぞれの記法が、プログラミング言語に当たるのだが、どれも説明を詳しく聞かないとパッと見ただけでは意味がわからない。

その結果、使われる言語(記法)が恐ろしく絞られている。

理系男子のバイブルと呼ばれている本で、ノーベル賞物理学者のリチャード・ファインマン(とその友人)によって書かれた「ご冗談でしょうファインマンさん」と言う本のなかに、ファインマンが独自の三角関数の記法を使っていたと言う話が出てくる。

ギリシャ文字の一部を引き延ばしてそこに数値を書き込むという記法で、引き伸ばされる線が右方向ならば正関数、左方向ならば逆関数になるようになっており、なかなか便利で気に入っていたそうだ。

しかし、友人にノートを見せた際、その独自の記法では全く伝わらず諦めて普通に三角関数を書くことにしたのだという。

これなどまさに現代であれば、「新しいプログラミング言語を作ろう」と思い立つ場面そのものなのだが、当時の時代の流れからして、若い物理学者が唐突に独自の記法を発明したとして、それを読んでもらえないと論文として意味をなさないので泣く泣く諦めた、というエピソードに見える。

数式にはメリットもあるのだがデメリットも多い。デメリットの最大のものは、数式をどうプログラムに展開していいか一見してよくわからないと言うことである。

例えば、力学で最もシンプルかつ重要な公式について例に出そう。

fは力、mは質量、aは加速度を表す

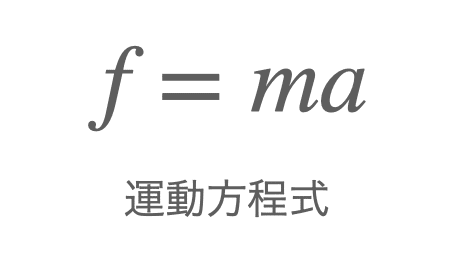
f=maは、極めて単純なしきである。
しかしこれをプログラムに変換して運動方程式を配慮した動きをプログラミングしろと言われると途端に難しくなる。

僕の場合、たまたま答えから先に勉強していたので難しくなかった。むしろ答えから数式を逆算したときに「こんなにすべてを省略していいのか」と思ったくらいだ。

答えは色々あるが、例えばこんなプログラムになる

f=1; // 力を1と定義する
m=1; //　質量を1とする
p = 0; // 座標
v = 0; // 速度
for(;;){
 a = f/m; // f=maをaについて式変形
 v += a; //加速度に速度を足す
 p += v; //位置に加速度を足す
}

f=maという式から、このプログラムを導出するのはそう簡単ではない。
まず、暗黙的に座標pと、速度vが出てくる。この二つがないと、そもそも運動方程式は意味をなさない。運動方程式が示しているのは、力と質量と加速度の関係だけだからだ。

加速度は、速度に対する差分であり、速度は座標に対する差分だ。
この問題は、速度と加速度の関係さえ知っていれば、小学生でも理解できる。

僕らの世代は小学生の頃にゲームを作るのが習慣になっている人が少なくなくて、ゲームを作ることで物理学に親しんでいった。

秋葉原プログラミング教室の教材では、最終的に「月がなぜ地球に落ちてこないのか」を運動方程式からプログラミングに落とし込むことで体験する。

僕もそうだったが、その瞬間にすべての意味を理解する必要はない。
高校生になって物理を選択し、運動方程式が出てきた時に、「あ!あれはこういうことだったのか」と分かればいい。それは体験を伴わないどんな学習よりも価値がある。これが本質的に「分かる」ということだと思う。

何が言いたいかというと、「分かる」ためには数式だけ見ていてもダメなのだ、ということだ。それでは応用できない。応用するためには、何を置いても触ることが大事なのだ。

学者だけが論文を読めばいいと言う時代であれば、「数式を読めないお前が悪い」で済んだのだが、もはやコンピュータプログラミングに数式が導いた結果を導入するのが当たり前の時代にそんなマッチョな話は通用しにくい。

何より、「数式が読めるだけ」では分かったことにならないのだ、というのがプログラマーの肌感覚だと思う。

これは物理学の世界でも、ずいぶん昔に発見された方程式が、できた段階ではその意味も解も分からず、時間を経てようやくその方程式の意味しているところがほかの研究者によって発見されるということからも想像できる。

何でこんなことを書いてるかというと、VisionOSのSDKがダウンロード可能になってなかなかダウンロードが終わらなくて「触らずにVisionOSのことが分かるものかよ」と思っている時間を何とか潰そうとした時に「やっぱり触らないと分からないよなあ」と思ったからである。