【集合論#3】ド・モルガンの法則

ド・モルガンの法則

(A∪B)ᶜ=Aᶜ∩Bᶜ
(A∩B)ᶜ=Aᶜ∪Bᶜ

この2つをまとめてド・モルガンの法則

AとBの和集合の補集合は、Aの補集合とBの補集合の共通部分

AとBの共通部分の補集合は、Aの補集合とBの補集合の和集合

ベン図を書くと明らか

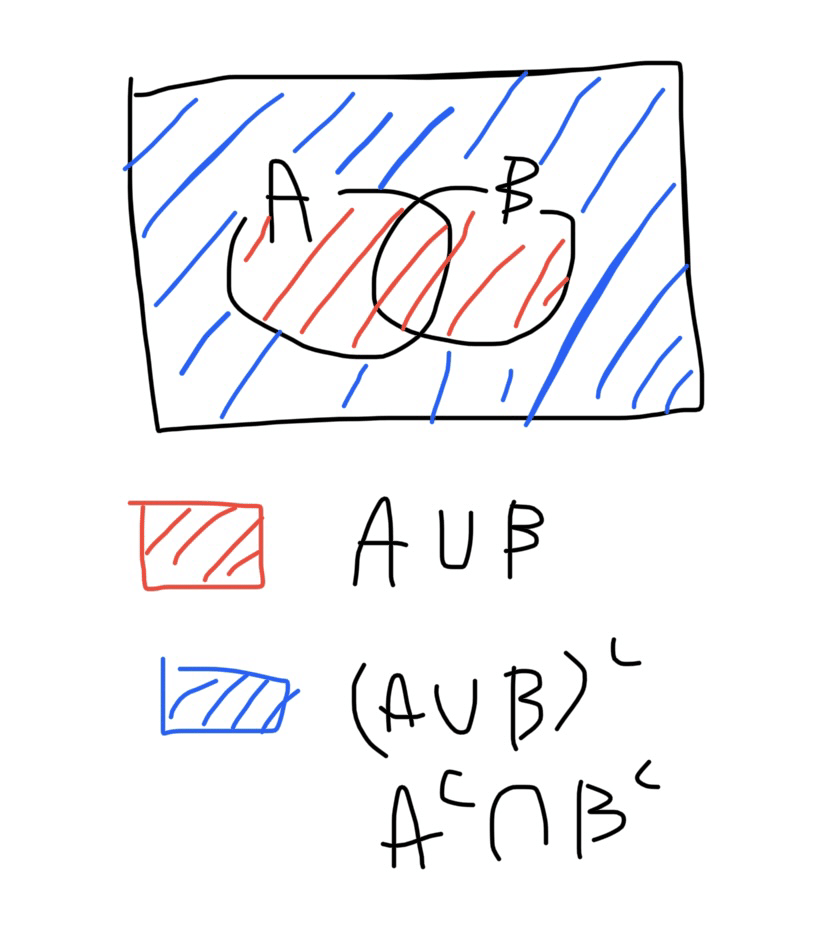
明らかといえど本当にそうなのか？
やはり証明が必要

証明

目標
イコールを示すから
①(A∪B)ᶜ⊂(Aᶜ∩Bᶜ)
と
②(A∪B)ᶜ⊃(Aᶜ∩Bᶜ)
の両方を示す

①の証明
x∈(A∪B)ᶜとする
A⊂A∪Bより
x∈Aᶜ
B⊂A∩Bより
x∈Bᶜ
xはこの2つを同時に満たさなければいけないので
x∈Aᶜかつx∈Bᶜ
つまり
x∈Aᶜ∩Bᶜ
(A∩B)ᶜの元が全てAᶜ∪Bᶜの元になったので
(A∪B)ᶜ⊂(Aᶜ∩Bᶜ)

②の証明
x∈(Aᶜ∩Bᶜ)とする
x∈Aᶜかつx∈Bᶜから
xはAにもBにも入っていない
x∈(A∪B)ᶜ
Aᶜ∩Bᶜの元は全て(A∪B)ᶜの元になるので
(A∪B)ᶜ⊃(Aᶜ∩Bᶜ)

①,②合わせて
(A∩B)ᶜ=Aᶜ∪Bᶜ
が証明された

もう1つも同じ理屈
もしくは
(A∩B)ᶜ=Aᶜ∪Bᶜ
の両辺の補集合をとることで
証明できる