【集合論#7】合成写像・逆像・逆写像

合成関数

f:A→B
と
g:B→C
という2つの写像があるときに
fでAをBにして、その後、gでBをCにする
とAからCへの写像ができる
g(f(x))

これを合成写像といい
g⚪︎f:A→C
と書く

例えば、
f:ℝ→ℝ
f(x)=2x
g:ℝ→ℝ
g(x)=x²
とすると

g⚪︎f(x)
=g(f(x))
=g(2x)
=(2x)²
=4x²

逆像

f:A→Bという写像はAの元aに対してf(a)を対応させた

逆にBの元bに対してf(a)=bを満たすaを対応させるものを考える

このようなものを逆像といい、a=f⁻¹(b)と書く
⁻¹は-1乗ではなく、逆のことをしたという意味
インバースと読む

例えば、
f:{1,2,3}→{1,2,3,4,5}
f(1)=2
f(2)=3
f(3)=4
という写像で

f⁻¹(2)=1
f⁻¹(3)=2
f⁻¹(4)=3
となる

矢印を逆向きに辿った

f⁻¹(1)やf⁻¹(5)は矢印が向いていないので存在しない

次にこのような写像
f(1)=1
f(2)=1
f(3)=2
f(4)=3
f(5)=3

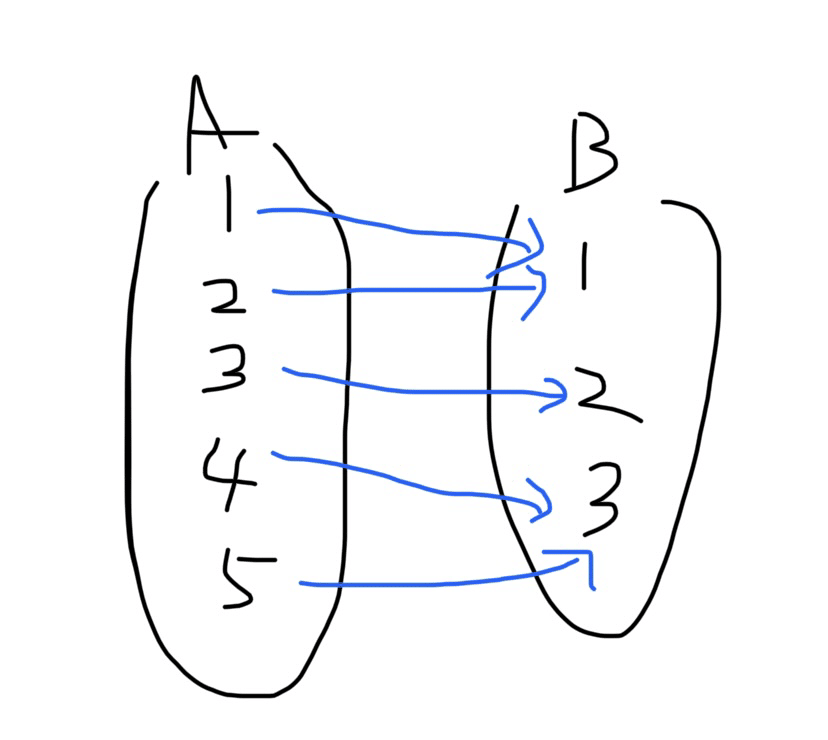
このとき、1から矢印を逆向きににたどると1と2の2つになる
なので、1の逆像は{1,2}の集合

f⁻¹(1)={1,2}

逆像が1つの時は、元が1つの集合とも見える
f⁻¹(2)={3}

最初の例で逆像がないものがあったが、それは逆像が空集合であるといえる

特に、0の逆像のことを核と言い、Ker(f)と書く
簡単に言えば、方程式の解のこと

逆写像

逆像は写像っぽく見えるけど写像ではない

写像A→Bは
Aの全ての元に対してBの元を対応させないといけない
Aのそれぞれの元はBの1つの元としか対応しない
というルールがある

先ほどあげた2つの逆像は、それぞれ満たしていない

逆像が逆写像になるには、単射であり、全射である必要がある
つまり全単射

単射であれば、1つの元から複数個の元を対応させることはない

全射であれば、全ての元に対応するものがある

f:A→B
f(x)=2x
とすると
fは全単射なので
逆写像
f⁻¹(x)=x/2
がある

写像と逆写像の合成写像は恒等写像になる
恒等写像とはf(x)=xのように自分自身を対応させるもの

f⚪︎f⁻¹(x)=x

行って戻ってきたら同じもの