主軸(回転対称軸ｎ)と縦,横の対称面m

m･n:m　雪の結晶，機械部品，日用品など

このタイプの対称性は，対称要素の数が多いにもかかわらず，その図形は非常にシンプルに見えます．それはおそらく，対称群の位数が高いためでしょう．ここであつかうm･n:mという対称性は，初歩的なよく知られている多くの図形に当てはまります．
対称m･n:mをもついろいろな図形：
正方柱プリズムm･4:m，正５角柱プリズムm･5:m，正3角双ピラミッドm･3:m，双円錐m･∞:m，シリンダーm･∞:m，回転楕円体m･∞:m

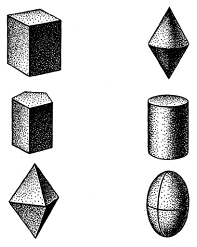
これらの図形の特徴は，いずれも，n回回転軸を特異軸（主軸）とし，それに沿ってn枚の縦の対称面mがあり，さらに，横の対称面mが，主軸に対して垂直に配置されていることにあります．
横方向の対称面と縦方向の対称面の相互作用から，横方向の対称面に平行なn本の２回軸が生まれます（図）．

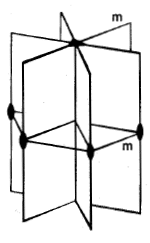
図は，対称クラスm･3:mの対称要素の配置を示す．垂直に配置したの3回軸（▲）にそって，3枚の対称面mが交差している．3回軸に垂直な対称面mがある．垂直と水平な対称面の交線は2回軸（黒い小楕円）である．

特に，位数が偶数の主軸の対称クラスには，対称心が現れる．これは，軸と軸に垂直な対称面との交点にできる．奇数位数の主軸の場合には，対称心はできない．

このタイプの対称性は，上と下，右と左，前と後ろを区別する必要がないものに適している．自然界では，果物や種子，小石などに見られ，非常に広く結晶にも見られる．特に，氷の結晶（雪の結晶）はこのような対称性を持っています（図）．

雪の結晶の形は実に多様で，BentleyとHumphreyが作成したアトラスには，1,000枚以上の写真が掲載されています．

この対称性m･n:mは，箱，タイル，レンガ，シャフト，チューブ，ナッツ，缶，コイン，鉛筆など，大量生産される技術的なものに広く採用されています．

記号m･n:mに現れる対称要素は，この群の生成元（群を生む対称要素）です：n回回転対称の主軸n，主軸に垂直な対称面m（：は主軸に垂直の意），主軸に平行な対称面m（･は主軸を含む面の意）．これらの極限群は，n=∞の場合で，m･∞:m．