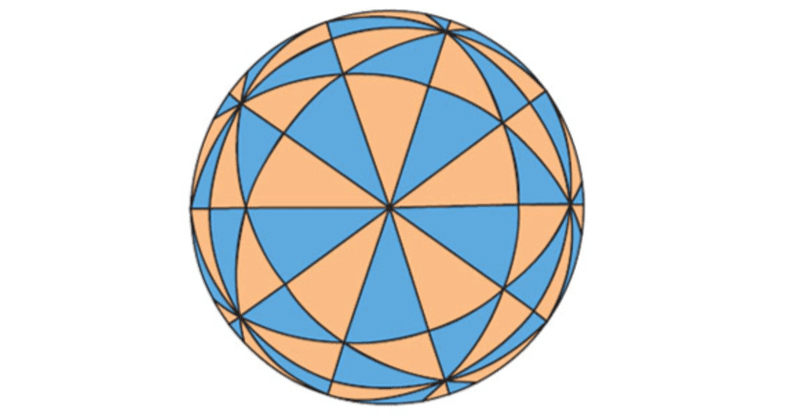
球面万華鏡と正多面体

正多面体を，球面万華鏡に対応させて考えることができます．Oを中心とした正多面体Mがあったとします．Aは正多面体のある面の中心，Bはその面の辺の中点，Cはその辺に属する2つの頂点のいずれかとします．頂点Oから発し，点A, B, Cをそれぞれ通過する辺が作る３角錐Kを，正多面体Mの基本錐と名付けます（図の場合は，立方体Mの例）．

面とその辺とその辺に属する頂点の選び方を変えれば，正多面体Mの様々な基本錐ができますが，それらは重なり合うことなく，空間全体を覆っています．基本錐の数Nは，以下のいずれかの計算で求めることができます．
N=2pG=4P=2qB
ここで，Gは多面体Mの面の数，Pはその辺の数，Bはその頂点の数，pは各面の辺の数，qは各頂点に集まる辺の数です．

したがって，立方体の場合は
G=6, P=12, B=8, p=4, q=3, N=48となります．

基本錐の面は，正多面体Mの対称面であり，共通の面を持つ2つの基本錐は，その共通平面に関して対称となります．例えば，立方体の場合，基本錐Kと基本錐K′は対称です．

基本錐KのエッジOAは，2p個の基本錐に共通なエッジです．したがって，エッジOAにおける基本錐Kの二面角はπ/pとなります．同様に，エッジOBの二面角はπ/2，エッジOCの二面角はπ/qであることが確認できます．したがって，任意の基本錐と正多面体Mの同心球面との交点は，鋭角π/pとπ/qを持つ直角球面三角形となります．こうして，球面万華鏡を作ることができます．

正多面体から球面万華鏡に移行するとき，基本錐のどの辺が面の中心を通り，どの辺が正多面体Mの頂点を通過するかの情報は失われます．もし，頂点が正多面体Mの面の中心となる正多面体M′を考えると，同じ球体万華鏡が対応します．このような正多面体MとM′は，互いに双対と呼ばれます．例えば，立方体は正八面体と双対です．正四面体は，自分自身に双対です．MからM′に移るには，数字のpとq，GとBを入れ替えます．

球面三角形で1/p+1/q+1/r>1を解いて，p,q≧3 の (p, q, r)の整数解を求める．
求めた(2, 3, 3), (2, 3, 4), (2, 3, 5)は，それぞれ，正4面体，立方体と正8面体，正12面体と正20面体に対応します．

球面三角形の面積は，その角の和からπを引いた値に等しいことが知られています．特に，鋭角π/pとπ/qとπ/2の直角球面三角形の面積は，(1/p + 1/q - 1/2)πになります．球の全表面は4πなので，ここから数Nの別の公式が導かれます:

N=４/(1/p+1/q+1/2)

n次元正多面体と(n - 1)次元球体上の万華鏡にも同様の関係があります．面白いことに，3次元空間では5つの正多面体がありますが，4次元空間では6つ，n＞4のn次元空間では3つの正多面体（４面体，立方体，８面体の類似体）しかありません．

引用：
E. B. Vinberg, published in the "Soros Educational Journal" (1997, No. 2)
«КВАНТ» No6, 2020