
網目パターンの重ね合わせ2
2つの同一な網目パターンを種々の回転角度で重ねたときの干渉で,何が起こるか考察しよう.例として,長方形の中心にも格子点のある(面心斜方格子)(図110d)の頂点に円環を配置した網目パターンの系をとり上げる.

Fig.159: 回転角小の間は二次的モザイク構造は,円環の一次構造を思わせる.

Fig.160:回転角が大きくなると,二次的像は一次の拡大像ではなくなる.二次的網目の対称性は,一次の網目の任意の回転に対しても変化しない.
図159と160を見ると,角度2θが小さいうちは,二次的図形は(素図形の数が不十分なために)一次図形の拡大図となることがわかる.角度2θが大きくなるにつれて,拡大の度合いは小さくなる.面心斜方格子の対称性を保ったまま,パターンは非常に大きく形を変え始める.図示された一連のパターンは,壁紙や織物に適するパターンの豊富なバリエーションが,異なる相対角度をなす2枚の同一の周期構造の単純な機械的重畳によって得られることを示している.この可能性を考えると,一連の疑問が湧く.例えば,同一の周期構造の負あるいは正の重畳によってどんな効果が得られるだろうか.実験を上記に記述したパターンで行うと,二次的に生じた6角形の各中心に暗い丸点が形成されることが判明した(図161).

図161:円環の正と負の系の干渉が,ハチの巣状の二次的像作り出し面心斜方格子の格子点に暗い場所がある.
特に興味深いのは,異なる図形を重畳したときの,対称性の相互作用に関する問題である.一般的な重畳や同一対称類の等価系の重畳,右手パターンと左手パターンあるいは異なる色に塗られた図形の相互作用などである(図162).
これらの問題は,ほとんど研究されたことがないが,我々は複合系の対称性原理を使い,これらを調査してみよう.この原理は12章で紹介する.

図162:非対称3角形(図154)の網目の右手と左手系の正の干渉は対称性を増加する.対称面は二次的周期構造に現れている.

図163:左手正と右手負による干渉.二次的な正方格子の点が現れている.
無限に繰り返すパターンの重畳で生じる二次的な形の多様性にもかかわらず,等式λ=2dsinθは成立している.ただし,そこでは同一網目2つの
のパターンが選択され,角度2θはあまり大きくない.
図163(正の左手系パターンを負の右手系パターンの上に重畳)では,二次的パターンが,一次のパターンの基底である正方格子を再現しているのが,はっきりわかる.後者は黒が正,白が負の小さい3角形の行からなる.
網目の拡大率(d/λの比)と角度2θは,互いに密接な相関がある図から決定され,この式が問題のケースに適用可能であることを示している.

図164
最後に,周期の異なる2つの縞模様の平行重ね合わせを考えてみよう(図164).これは,音響学,光学,無線技術,その他の波動物理の分野で出会うビート現象幾何学的な描像を提供し興味深い.
この現象は,同じ方向に移動する波長がわずかに異なる2つの平面波が,二次的に長い波長の波が生じる現象で,音響学的には周期的な音の強弱(ビート)として観測される.ビートは近似的に調整された2つの音叉を同時に鳴らすことで簡単に作れる.実際には,2つの同じピッチの音叉の一方だけに,ワックスを貼り付けてチューニングをずらす.
平行な2つのシステムの重畳で生じるビートは,図164に示すように,第1のシステムの隣接する2本の縞の間隔λ_{1} = 1.91 mm;第2のシステムのこの間隔λ_{2}=1.60mmとすると(これらの2つの量は,一次干渉の波長と呼ばれることがある),距離L=9.86mmは,密な隣接距離で,二次的な波長あるいはビート波の波長と同じである.
これらの量の関係をより詳細に検討すると次の式が得られ,既知のλ_{1},λ_{2}から,二次波の波長Lを計算することができる:
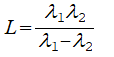
この記事が気に入ったらサポートをしてみませんか?
