
タイルとHeesh数
Haydar Nurligareev "Kvantik"# 10,2019より.Alexey Weiner画
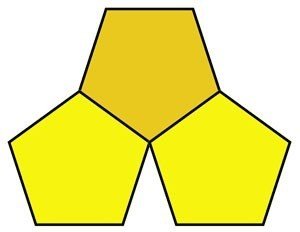
正3角形,正4角形,正6角形は,それぞれ無限に広い平面をタイル張りできます(図1).1つのタイルを置きその周囲をタイルで取り巻きます(レイヤー1).次のその周りを取り巻きます(レイヤー2).以下同様に無限に続けられるので,正3角形,正4角形,正5角形のHeesh数は∞といいます.

正5角形のタイルはタイル張りできません(図2).正5角形のHeesh数は0です.
ランダムに選択されたタイルにもHeesh数があり,通常は0または∞のいずれかです.Heesh番号が1,2,3,...の多角形はありますか?1968年にハインリッヒヒーシュHeeshがこの問題を定式化する前は,Heesh数が0か∞以外の既知のタイルは1つしかありませんでした(図3).このタイルは多角形でさえなく,1922年にWalterLitzmanの著書「AmusingandStrangeNumbersandShapes」に最初に登場しました.

Heesh自身が,Heesh数が1に等しい別のタイルを見つけました.これは,正方形,通常の三角形,および同じ三角形の半分で構成される5角形です(図4).

Anne Fontaineは,1991年にHeesh数が2のタイルの最初の例を示し,そのようなタイルを無数に作成しました.それらはすべて同じ正方形で構成されています.つまり,それらはポリオミノ図形です(図5).

同じ年に,ロバート・アンマンは通常の6角形に2つの突起を追加し,同じ溝を3つ切り取り,Heesh数が3の図を作りました(図6).アンマンのアイデアはシンプルでエレガントです.突起と同じ溝があるタイルを探す必要がありますが,その数は異なります.

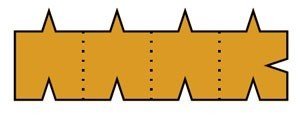
2001年にCaseyMannによって発見されたタイルの例を使用して,このアイデアがどのように機能するかを示しましょう.これは,4つの突起と5つの溝を持つ4セルの長方形の形をしています(図7).そのようなタイルのHeesh数が大きすぎない理由を以下で述べましょう.タイルのコピーで完全に覆われた正方形Sを考えてみましょう.各溝は同じ突起でしか閉じることができないため,正方形Sの内側にある溝と突起の数は 同じです.一方,正方形内の突起の数は、その面積(セル内)にほぼ等しくなります-タイルの各セルには突起が1つだけあり,溝の数はその面積の5/4にほぼ等しいためです-タイルでは,4つの突起ごとに5つの溝があるためです.しかし,大きな正方形では,これらの数を等しくすることはできません.
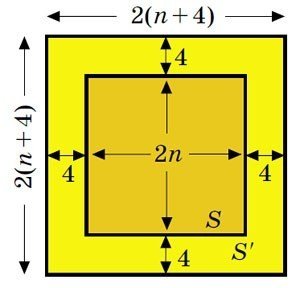
サイズ2n × 2nの正方形 Sをタイルで完全に覆います。これには少なくとも2n・2n/4=n^2のタイルが必要です.それらには合計5n^2の 溝があり,すべて埋める必要があります.一方,これらのスロットは2(n+4)×2(n+4)の正方形S 'の内側にあります(図8).したがって,2(n+5)2(n+5)個以下のセルからの突起で埋められます.したがって,突起の最大値は2(n+5)2(n+5)= 4n^2 + 40 n +100です.n > 100の場合,不等式n^2 > 40n + 100は確実に満たされ,5n^2 > 4n^2 + 40n + 100,つまり,突起よりも多くの溝があります.矛盾-すべてのスロットを埋めることはできません.したがって、このタイルのHeesh数は有限です.実際には3に等しい(図9)が,これまでのところ,コンピューター検索によってのみ証明することができます.

フィギュアを研究するのに最も簡単なのは,ポリオミノ,ポリアマンド, ポリヘックスです.それらはまた,互いに隣接する同じ「セル」で構成されており,ポリアマンドではセルは通常の三角形で,ポリヘックスでは通常の六角形です.ポリオミノ,ポリアマンド,またはポリヘックスからタイリングするときは,「市松模様」の紙にレイアウトします(図1).このような紙では,コンピュータ検索を整理するのは簡単です.これが,Casey Mannケーシー・マンがHeesh数3のポリアモンドを見つけた方法です(図10).

また,ケーシー・マンはHeesh数が有限であるがゼロに等しくない,突起と溝を備えたいくつかの新しい一連のポリオミノとポリヘックスを何とか入手しました.これが,ケーシー・マンのポリヘックスで,5つの六角形(突起と溝付き)で構成されています-このHeesh数は5で(図11),今日人類に知られている最大の有限のHeesh数を持つタイルです.

この記事が気に入ったらサポートをしてみませんか?
