実用的無限大

「幾何級数（指数関数）的に成長する」という言い回しは，日常語でよく使われる．
数列 $${\{b_1, b_2, b_3, ……..\}}$$で，$${b_{n+1}=b_{n}q}$$のような数列を幾何級数と呼び，$${q}$$は公比である．次のようにも書ける$${b_n=b_1q^{n-1}}$$
$${q>1}$$なら数列は増加し，$${1>q>0}$$ なら数列は減少する．

幾何級数的に説明できるいくつかの例を見てみよう．
１．
チェスの起源に関する最も有名な伝説がある．
昔々，古代インドで，セッサという賢者が新しいゲームのルールを考案し，シェラム王にプレゼントした．
王は魅了され，ゲームの考案者に自分の報酬を選ぶよう招いた．彼は自分の報酬を次のように選んだ．王様は，ボードの最初のマスに小麦を1粒置く，2番目のマスに2粒，3番目のマスに4粒というように，次のマスには前のマスの2倍の麦粒を置かなければならない．幾何級数的な増加である．$${b_1=1}$$，$${q=2}$$という「ささやかな」要求を満たすことは不可能だった．地球全体の収穫を何千年もかけて行わなければならない量である．

２．
幾何級数の想像を絶する成長は，ただ紙を折るだけでも感じることができる．二つ折りにすると紙の厚さは2倍になり，それを二つ折りにすると4倍になる．すぐに実践できる実用的な可能性がなくなってしまう．
一枚の紙を42回折ることができたと仮定すると，その厚さは地球から月までの距離よりも大きくなる．

３．
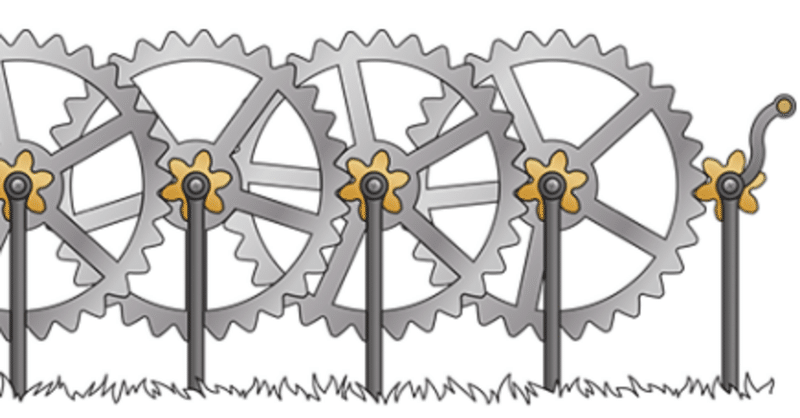
数列が減少する性質の例：冒頭の図のように歯車の連鎖を作ってみよう．

歯車の連鎖は前の連鎖の5倍遅く回転するとする．
この連鎖は十分に長いと仮定する．もし，最初の歯車の車軸を高速で回転させ始めたとしても，最後の歯車は実質的に回転しない．
例えば，連鎖に17個の歯車があり，最初の歯車が1秒間に1回転するとすると，「20年後」最後の歯車は1/1000回転もしない．だから，壁に永久に固定したも同然である．この先何年もの間，動かないのだ！
これは儚い人間の人生から見れば，実用的無限といえる．
「指数関数的に成長する」という表現は，これに非常に近い意味を持つ．

もしパラメータ$${n}$$が離散時間であるなら，$${b_{n+1}=b_1q^n}$$の式は，時間における量の急激な変化の記述とみなすことができる．高速連続過程では，$${y(t)=bq^t}$$の形の関数が現れ，これは指数関数と呼ばれる．したがって，関連する用語は指数関数的成長である．

応用：私たちを取り巻く世界
数学：幾何級数

『数学的構成要素』p.94-95より抜粋