コーシー-リーマンの方程式

コーシー (1789-1857)、リーマン (1826-1866)
これも19世紀の数学で重要な発見の一つです．数学が社会（科学技術も含まれる）とどのような係わりを持つかを知るのが私たちの目的です．数学の勉強会ではありませんが，複素関数論は19世紀に確立した重要な分野ですし，広い応用分野をもちますので，その基礎となる概念とはどのようなものでしょうか．お付き合いください．
私たちの使う関数論は19世紀の数学で十分なようです．Fourierフーリエ級数（変換）,Laplaceラプラス変換を取り上げましたが，複素関数に少しだけ言及します．今回は，コーシー-リーマンの方程式を見てみましょう．
数学の勉強会が目的ではないのでできるだけ言葉で説明します．

複素平面（x軸が実数，y軸が虚数）に定義域Dをもつ複素関数f(z)を考えましょう．この関数は領域Dで正則（微分可能）であるとします．微分可能な関数ですから，連続であることはいうまでもありません．
複素平面は2次元ですから，ある点zでの微分は，ｘ軸に沿って（xで偏微分）行う微分係数と，y軸に沿って（yで偏微分）行う微分係数がありますが，複素関数が正則であるとすると，どちらの微分係数も一致し，点zでの微分係数は確定しなければなりません．関数がDで正則とは，定義域Dのすべての点で微分係数が確定する（微分可能）ことです．

逆に，コーシー-リーマンの方程式が成立するなら，複素関数f(z)は正則であることが証明できます．

従って，複素関数が正則であるための必要十分条件は，コーシー-リーマンの方程式が成立することです．

■正則な複素関数　f(x,y)＝u(x,y)+iv(x,y)　はその実数部u(x,y)あるいは虚数部v(x,y)のどちらか一方を知れば他方は決まってしまう．

例えば，虚数部v(x,y)を知り，コーシー-リーマンの方程式を使うと，実数部u(x,y)を求めることができる．例えば，以下のyoutube動画には，このような問題の演習があります．

■応用について
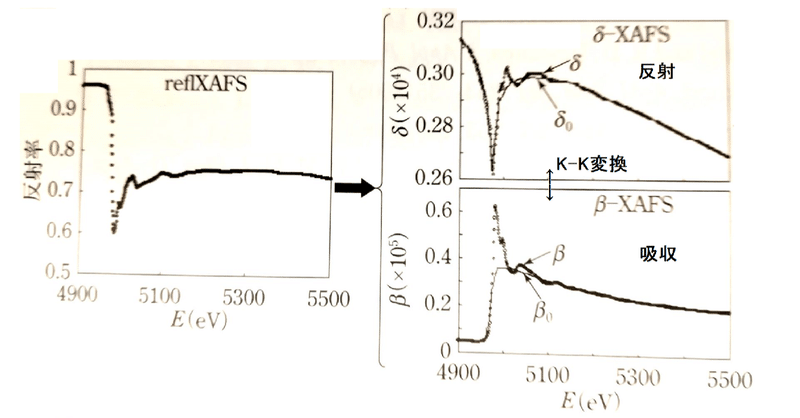
ちょっと数学から飛躍しますが，実部を知って虚部を求める例として，私のやった実験の話をします．