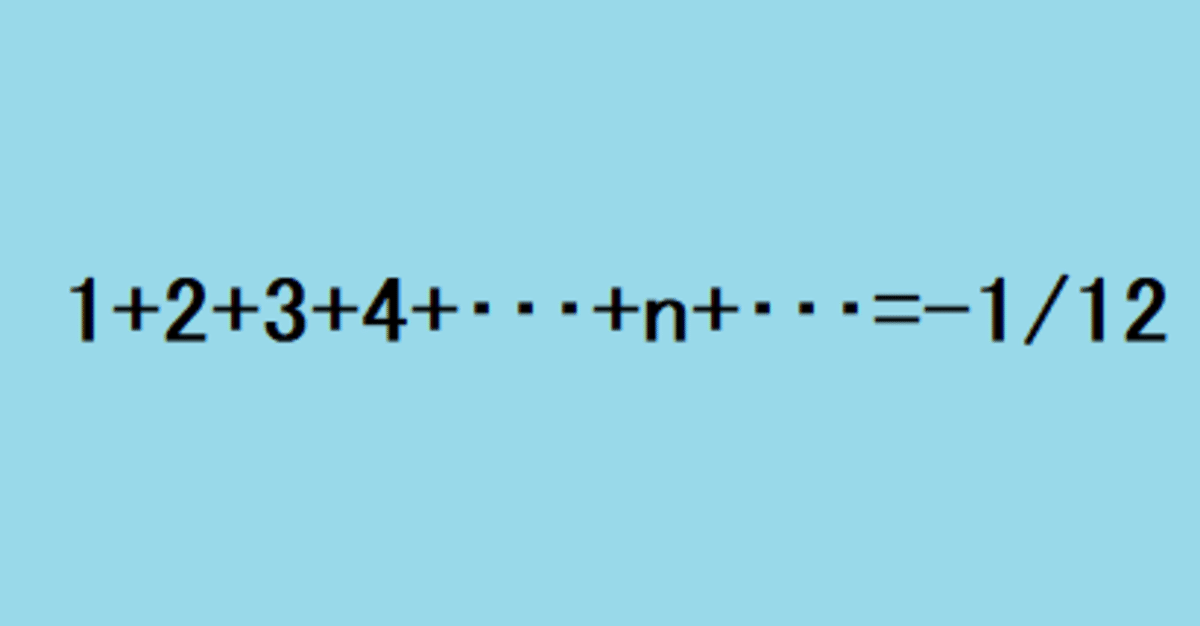
無限の脅威

まぐまぐに投稿したメルマガ（html版）のリメイクです．
数式は見やすく表示されていますか？添字の不統一が気になる方は，tex表示を用いている　数学月間の会HP　を訪問ください．

━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 ［2014.05.09］ No.002
<<数学と社会の架け橋＝数学月間>>
━━━━━━━━━━━━━━━━━━━━
■無限の脅威（2014年米国MAMの話題より）
http://www.mathaware.org/mam/2014/calendar/infinity.html）
今回は，奇妙な数学の話です．

■発散する級数

正の整数すべての総和が無限大でなく-1/12であるという．正気の沙汰なのか？　このとんでもない結果は，1748年に偉大なオイラーにより導かれた．
発散する数列は悪魔の発明であり，無限級数を用いると，どんな結論でも導くことができる．
発散する級数の研究は，アーベル（1802-1829）に端を発する．
数学者がこの悪魔の細部を解決するのに続く百年を要したのだ．
すなわち，リーマンの解析接続の理論(1859)を待ち理論的に解決した．
現代では，物理学（超弦理論,量子計算）や数学（ζゼータ関数）でこの結果を利用している．
リーマンは素数の分布を調べるためにζ関数に解析接続をした関数の0点を研究し，リーマン予想を提示した(1856）．これはまだ解かれていない．

■オイラーの発見が現実に
オイラー＋リーマンの ζ関数は無限級数の形で定義される．

この関数は，実部が1より大きいRe(s)>1複素平面で収束するが，
実部が1あるいは1より小さいRe(s)=<1複素平面では発散する．
（複素数sの実部が１よい大きいとき収束で，実部が1あるいは1より小さいとき発散）

そこで，全複素平面（ただし１は極）に，ζ 関数の定義域を拡張
するのに解析接続という手段が役立つ．

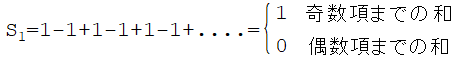
この和S_1は，偶数項で止めれば0，奇数項で止めれば１になる．
しかし，解析接続という理論を使うと1/2になることを以下に示す．

この多項式は公比x の等比級数だから，|x|<1 なら収束し,1/(1−x)になる．
もとの多項式は|x|<1の外では発散するので定義できないが，
級数を解析接続した関数1/(1−x)に繋ぎ，形式的だがx=−1を入れると, 1/2 が得られる．

級数 S_1,  S_2 などを数式と見立て加減演算をし，Sを求めてみよう．
∞+∞などの無限大を数値のように演算しているのが気持ち悪いが
解析接続で収束した級数を用いているので実は正しい結果になる．

■参考
http://www.mathaware.org/mam/2014/calendar/infinity.html
超弦理論入門，大栗博司，ブルーバックス
リーマン予想を解こう，黒川信重，技術評論社