ロビンソン・モザイク

この記事は，主として以下の記事の図を引用しながら，非周期のロビンソン・タイリングの顛末を筆者が解説したもので，翻訳ではありません．

Хайдар Нурлигареев，«Квантик» No10, 2020より
https://elementy.ru/nauchno-populyarnaya_biblioteka/435866/Mozaika_Robinsona
図Алексей Вайнер

何種類かのポリゴン（多角形）タイルよりなる有限集合があり，各ポリゴンタイルのコピーは好きなだけ作れるとします．そのようなコピーを隙間なく並べて平面全体をタイル張りします．たまたま，図１のタイル張りは，ポリゴンが1種類で構成されたもの（左図はクロス・ペントミノ図形だけ：右図は正6角形だけ）ですが，得られるタイリングは周期的になります．しかし，ポリゴンが1種類だけであっても，（例えば，正方形のみ，あるいは，正三角形のみの場合），タイリングは周期的にも非周期的にも作れます（図2）．

図１

図２

2次元の「周期的」タイリングとは，非平行な２つの方向への周期的な平行移動でタイリングパターンを自分自身に重ねることのできるものです．

驚くべき事実は，平面を非周期的にのみタイリングする図形集合が存在することです．20世紀半ばに（1966年），ロバート・バーガーが20,426個の異なるポリゴンタイル集合を用いて，最初のそのようなタイリングを作るまでは，このようなポリゴンタイル集合は存在しないと信じられていました．少し後，バーガー自身が，このポリゴン集合の数を104個に減らし，次の10年間で，多くの科学者の努力により，ポリゴン集合を2個にまで減らすことができました．2種類のポリゴンタイル集合より構成されるモザイクの発見はペンローズによってなされました．平面を非周期的にのみタイリングする単一のポリゴンがあるかどうかについてはまだ不明です．

次の6つのポリゴンの集合は、1971年にRaphael Robinsonによって提案されました（図3）。

これらの6種のタイルのみを用いて平面をタイル張りした例です.

少なくとも1つのタイル Aがタイリング中に必ずあるはずです(その理由はコーナーの突起に注目）．そのタイルAの向きは赤い線が右と上に出ていると仮定しましょう．これに隣接するのはタイルAでないことは明らかです．それでは，以下の図で？の位置にどんなタイルが置けるでしょうか？どちらの？の位置にもタイルAがないと仮定すると ，上側の？の右隣と右側の？の上隣りは両方ともタイル Aでなければならず，角が重なり合います．それゆえに，2つの？の少なくとも１つはタイル Aです．

タイルAが，タイルの右側の？にあると仮定し ます．すると，それらの間のタイルはCまたは Eとなり，2番目のタイルAは90°回転して赤い線が 左と上に突き出る向きになります（下図）．いずれにせよ，タイルAの間の上部中央はBの形の空きができます．

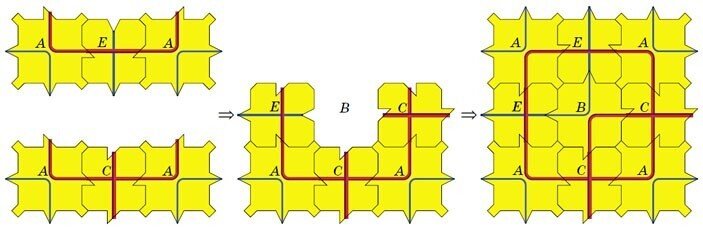
2つのタイルAの斜め上のタイルはBです．タイル Aと Bの辺は繋げて並べることはできません．タイルAは，自分以外の3つのタイルと角で隣接し，3×3の正方形の４つの隅にはタイルAがあり，それぞれの隅のタイルAは90°づつ回転してい ます．4つのAタイルの赤い線が向かい合って(赤い線の正方形ループができる)のがわかります．

タイルBは90°づつ回転した4つ方位がありますが，赤い線が繋がるような1つの方位に決まってしまい，3×3の正方形の中のタイル配置は一意に決まってしまいます（図7）．この正方形3×3で構成されたマクロタイルを，スケールを上げて，タイルAとまったく同じように見做すならば，7×7の正方形の角にそれぞれ90°づつ回転したものを配置することができます．マクロタイルの側面の中点から現れる赤い線は，お互いを結ぶ正方形のループになることも同様です．そして，タイルBは再び中央に配置される必要が あり，その4つの方位のうちのどれか1つに固定すると，残りのギャップは一意に埋まり，スーパーマクロタイルになります（図8）．

この統合プロセスはスケールを上げ（視野を拡大して）さらに継続できます．このようにして，サイズ1×1，3×3，7×7，15×15，31×31，...，（2^n-1)×(2^n-1)，....の階層的な正方形が作成されます．描かれるパターンは，２つの側面（左と下など）中央に伸びる2本の赤い線が作ります．

赤い線のループは，サイズが2×2，4×4，8×8，16×16，32×32，...，2^n×2^n，.....の正方形の階層になります．これらはロビンソンタイルの驚くべき特性を説明しています．

ロビンソンタイルを使用した平面のタイリングは非周期的です．非周期でないとすれば，タイリングパターン全体を移動して，違いがわからないように重ねることができるはずです．赤い四角は同じ赤い四角に移動する必要がありますが，ロビンソンタイルを使用したタイリングでは，どんどん大きな赤い正方形があらわれ，同じサイズの正方形どうしは互いに交差しません．結局のところ，どこまで移動しても，それを超えないほど大きな正方形があらわれ，周期はできません．

つづく