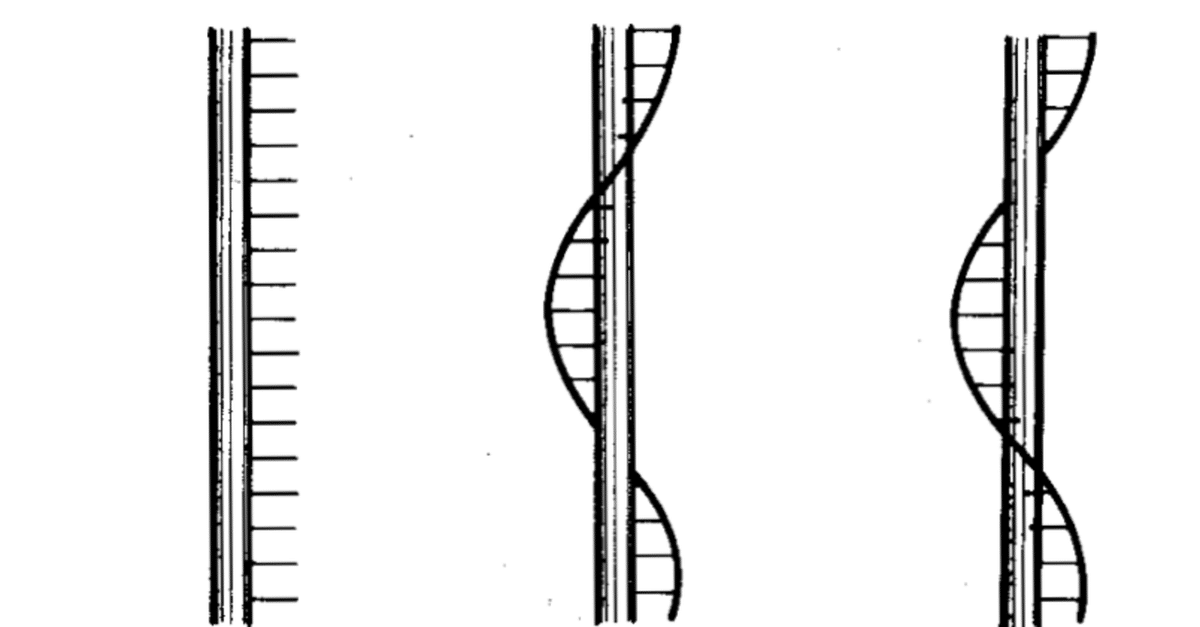
ロッド（棒）の対称性

図形のカテゴリー別にその対称性を調べるには，図形の対称操作で不変である「特異点」，「特異平面」，「特異軸」などを要請して，この要請を満足する「対称操作」の集合を，その図形の対称類とした．

有限図形の1点を特異点とするのが「点群」，1次元の並進軸や，2次元の並進軸をもつ「1次元空間群」，「2次元空間群」も作れる．

周期的図形であるが，特異平面を持つという要請を捨て，特異軸の存在要請を残した図形のカテゴリーは，ロッド（棒）のタイプである．

特異軸は，ロッドの軸で，このカテゴリーの図形の対称性には，並進軸の他に，単純回転，映進，任意位数のらせん軸がある．

ロッドのカテゴリーには，チューブ，ネジ，鎖，編まれた紐，コード，ビーズ紐，植物の茎，光線（偏光，非偏光），音波，種々の力線，数学のベクトルやテンソル（狭義の），等々がある．

■スクリュー対称軸の整合と非整合
ある有限図形が，回転軸に沿って角度αの回転と距離tの平行移動という2つの連続した（あるいは同時に起こる）操作の後に，始めの図形と完全に一致するなら，その図形は「スクリュー対称軸（あるいはらせん対称軸）がある」と言います．
ロッドの場合，角度αは必ずしも360°を整数で割ったものに等しい必要はないのだが，もしそのような場合は，α=360°/n，（ｎ：整数は，らせん軸の位数という）．　

例えば，このα＝60°なら，らせん軸の位数は６で，6回らせん軸：6_{1}, 6_{5}，これはねじの回転の向きに右回転と左回転に対応する．
ただし，位数２の場合のみ（あるいは，位数２のらせん軸を含むらせん軸），右手と左手の違いはない．

らせん軸の移動距離tは，a軸にそっての単位並進（格子定数）aとは別物なので，混同のないように注意せよ．特別な場合を考えると，αが1回転のときt=aとなる．周期的な結晶空間では，らせん軸は，2回，3回，4回，6回に限定されるが，ここでは，α→０，t→0の極限での「らせん軸」を導入する．これを，∞で表し，左回転と右回転の2種類の極限がある．