反転の利用ーパップスの定理

■円による反転鏡映の性質

①反転円の円周上の点は，反転しても元の点と同じ位置．
②反転では，円は円に変換される（直線も半径∞の円の仲間）
下図に反転円（赤い円）による，反転鏡映の例を示します．
●図１・反転円Oと交差する円Cは，交差の２点を共有する円cに変換される．
●図２・反転円Oと直交する円Cは，自分の上に変換される．
円周に直交するような反転円で分断された円の２つの部分は，反転円によるそれぞれの鏡像になる．
●図３・反転円Oの中心を通る円Aは，直線aに変換される．
特に，円Bが反転円Oと交差する場合は，交差する2点をよぎる直線ｂに変換される．
③反転円が直線なら，普通の鏡映像になります．
直線鏡の組み合わせで作られる映像は，良く知られた万華鏡です．
反転円を用いたアポロニウスの窓も拡張された万華鏡の映像と言えるでしょう．

■反転円の利用

反転の性質を使うと，パップスの定理の様な難しいものを簡単に証明できます．

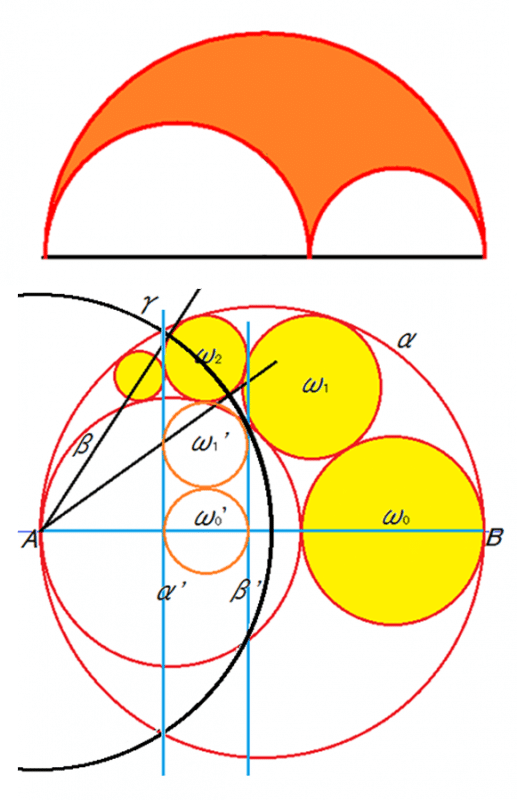
このような図形はアルベロス（靴屋のナイフ）といいます．
この中に面白い幾何学があります．

円弧αと円弧βに挟まれたアルベロスの領域に，互いに接す
るように円のチェーンω0, ω1,ω2, … があるとき， 円ωnの
中心と直径ABとの距離は円ωnの直径のn倍である．
（パップスの定理）

［以下の証明ができます］
円ω2の中心は，線分ABから円ω2の直径の2倍だけ離れていること．
① 点Aから円ω2へ接線を引く．両接点を通りAを中心とする円γは，円ω2
と直交します．（なぜなら，円の接線は接点での半径と直交するから）
② γを反転円にして，色々なものを反転してみましょう．
円ω2 は自分自身に．円α，β は，それぞれ 直線α’，β’に，
円ω1，ω0 は，それぞれ円ω1’，ω0’に，なります．
③ 円ω2，ω1’, ω0’の直径はすべて同じだから，パップスの定理が証明
された． （なぜなら，平行な直線α‘とβ’に挟まれているから）