特異点のある図形の対称類

対称要素の球面投影とステレオ投影

１つの特異点を持つ図形の対称類．

図形に対称心があるならば，それは特異点と一致しなければなりません．そうでなければ，（その特異点とは別に対称心があるなら），特異点の同価点がもう一つ生じ，特異点ではなくなります．
もし，図形に対称面と対称軸があるならば，それらが特異点で交わる必要があります．そうでなければ，特異点は対称要素によって繰り返され，複数生じ特異点ではなくなるからです．
特異点を球体の中心とすると，対称軸は球体の表面と正反対の2点で交差し，対称面は大円（子午線）に沿って球体の表面と交差するが，対称心は常に球の中心と一致します．
単純回転軸と球表面との交点には，軸の位数に等しい辺数の小さな黒の多角形で標記し，対称面と球表面の交線を太線円弧で標記し，対称心を小さな白い円で標記します．このような図は，図の対称要素の（3次元の）球面投影といいます．
3次元の球面を平面に変換投影すると有用な場合があります．
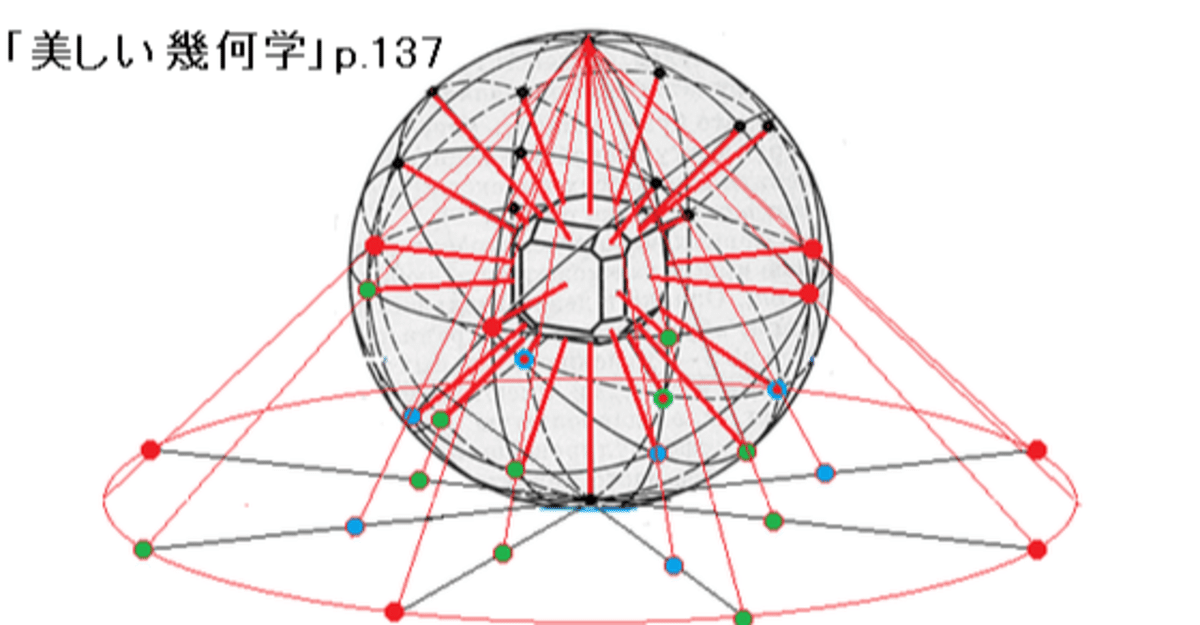
球面上の対称要素の出現点を，一定の規則に従って，球の赤道面に投影すること方法が，ステレオ投影です．
この投影は，地図製作と同様に，北極または南極から球面上の任意の点に引かれた光線によって行われます．
この光線と赤道面との交点は，球面上の点のステレオ投影像で，円弧や直線は対応する対称面の像となります．

対称要素のステレオ投影図を見ると，その対称類にどのような対称要素がいくつあるか，また，これらの対称要素が互いにどのように配置されているかを図から直接判断することができます．（表A）
このような図は，対称性を表すのに使う記号に比べて，わかりやすいのが利点です．
対称要素の記号は，投影図に付記されています．対称類の記号には，すべての対称要素が含まれているわけではありません．対称類を生成する対称要素だけが含まれ，それらの対称変換を用いることで，その類の他の（派生する）対称要素をすべて生成できます．
対称類のうち6つについては，次の関係があります．
~2=-1, ~2･m=2:m, 3/4･m=~6/4, 3/5･m=3/~10,
3/2:m=~6/2, 3/2･m=3/~4

（最後の2つのケースは，軸3に対す対称面mの向きが異なる）．
表Aでは，これらの対称類と，１つの極限類∞/∞･m=~∞/∞に対して，これらの関係の右辺に表示されている記号（慣用的に使用される）を使用しました．形式的な理由から，最も単純な4つの対称類には，それぞれ2つの同価な表記（図B）
2=1:2, 1:m=1･m, 2:m=~2･m, 2･m=m･1:m
があり，表Aの中では2回繰り返し現れており，紙面に対する対称要素の2つの異なる方向に対応しています．
これらの形式的な考察は，片面および両面のロゼットの対称類を考えるときに大きな役割を果たします．これらについては次の節で述べます．
特異点を持つ図形を特徴づけるすべての対称類は，結晶学では，「有限図形の対称類」と呼ばれ，対称変換の集合を点群と呼びます．

表Aは，これらの対称類を8つの列に分けて表示したものです．最初の7つの列は，対称が増加していく無限系列で，最後は，対応する記号の極限対称類を示しています．興味深いことに，2番目と3番目の列，そして6番目と7番目の列で極限類が同一であることです．
表の8列目には，正多面体の対称要素の投影を載せ，球対称の2つの極限類の記号を記しました．

図A

図B