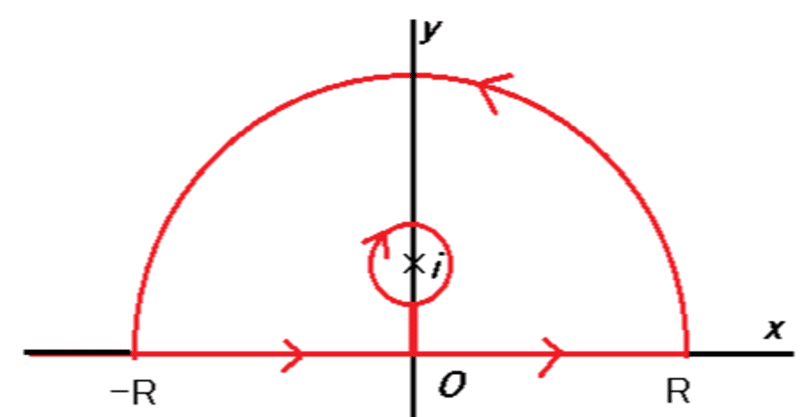
コーシーの積分定理
■コーシーの積分定理
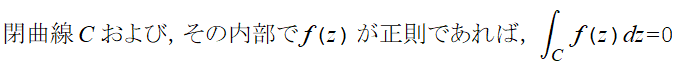
■ローラン展開と留数
関数G(s)に,極(分母が0となる特異点)がある場合,例えば,1つの極s1の周りで,次のようにローラン展開ができます.s1がn次の極とすると,
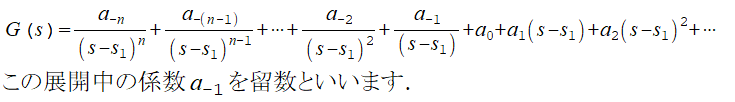
実は,G(s)を複素関数と見たとき,極s=s1で,G(s)は正則ではありません.s=s1を内部に含むような閉曲線Cに沿って左回りに1周G(s)を積分すると
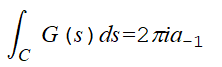
となります.これを留数の定理といいます.
さてこの証明は,難しくはありません.興味おありでしたら,親切な解説をしているyoutube動画(以下)がありますので,そちらをご覧ください.
関数をローラン展開すると,いろいろな次数の項がでて来ますが,閉曲線に沿って1周積分すると,なぜ,-1次の項の係数(留数)だけが残るのか不思議ですね.証明をyoutube動画で確認ください.たいへん都合の良い便利な性質です.
いろいろな場面で,いろいろな積分をするのに,留数定理を使います.「道具としての数学」の面目躍如です.複素関数論はいろいろな分野でとても活躍しています.
■話は変わりますが,ローラン展開の留数を見つける手法と一寸似た手法で,ラプラス逆変換をするときに,部分分数に展開できます.以下の例題をご覧下さい.
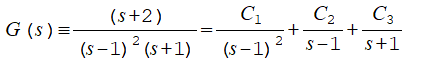
答えは,C1=1/2,C2=-1/4,C3=1/4 です.うまく見つけられましたか.
この記事が気に入ったらサポートをしてみませんか?
