ユニット折り紙塗り分け

24枚のユニットで作るユニット折り紙の立体は下図のようなものです．
4回回転対称軸，3回回転対称軸の主なもの（全部ではありません）を記入しました．2回回転対称軸や鏡映面もありますが略しました．探してみてください．例えば，緑色の3回回転対称軸は，図形の3回対称性を保存するわけですが，色に関しては，緑色を保存し，青→黄→ピンクの3色を置換します．
青色の3回回転対称軸は，青色を保存し，黄→緑→ピンクの3色を置換します．このように，ユニット折り紙の色（ユニット）の配置を，図形の形の対称性と矛盾しない配置とする方法を考えましょう．

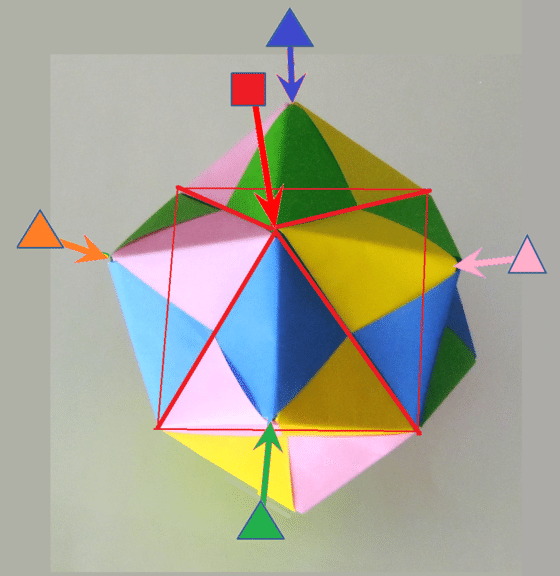
この立体の形は，正8面体の面（赤線で描いた正3角形）の上に，
ピラミッド（頂点は直角三角形面の直角が3つ集まっている）が乗っている形です．
これから作る展開図では，ピラミッドは正8面体の面（正3角形）に
射影されているので，頂点はぺちゃんこ（平面図）です．

正8面体の展開図の各面を，このように塗り分けるようにユニット（各色が1つのユニット）折り紙を組み立てると，正8面体の各頂点のある4回回転軸（x,y,z軸の方向に3本ある）で4色置換が起こり，正８面体の面の真ん中を通る3回軸（4本ある）は，1色は保存し，残る3色を置換する3回軸だということがわかるでしょう．もちろん辺の真ん中を通る6本の2回軸の色置換も完璧です．

このような色の配置は実際にユニット折り紙で実現可能です．作ってみてください．ユニット折り紙の規則では２つの直角3角形ピラミッドをつなぐユニットは1つのみですから，展開図の正３角形の面内の垂直2等分線を越えて同色の配置を１つ作ります．残りは，垂直2等分線の両側で分かれる別々のユニットになります．４色のバリエーションはいくらでもできますが，
配置に関しての解はただ一つのようです．
ただし，ユニットの作り方で右回りと左回りのものがあります．

この立体を眺めると4回軸の周りに，4つの色の帯の大円（緑，黄，青，ピンク）が見えます．各色の帯の大円は，各3回軸を地球の地軸と見立てたとき赤道に相当します．そして，その3回軸が保存する色が，帯状に現れるのです．

この立体には4色置換が行われる4回回転軸（3本）があり，外から（x,y,z軸の正方向）見て右回りに以下の順です：
x軸：黄→ピンク→青→緑，
y軸：黄→ピンク→緑→青，
z軸：黄→青→ピンク→緑

3色置換が行われる3回回転軸（4本）があります．
z軸（ｚ>0方向）の外から見て右回りに以下の順に置換が起こります：
黄→緑→青（保存：ピンク），黄→緑→ピンク（保存：青），
ピンク→青→緑（保存：黄），黄→ピンク→青（保存：緑）

■正20面体（あるいは双対な正12面体）
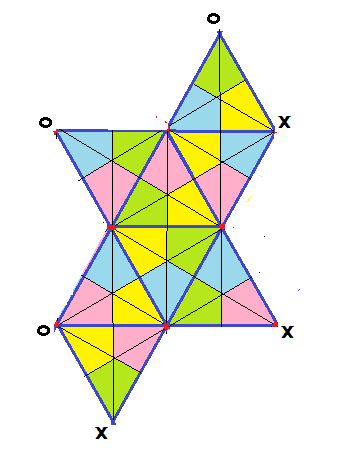
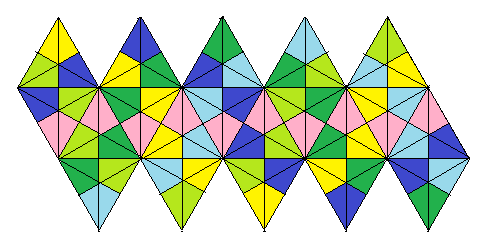
60ユニット（正20面体の面の上にピラミッドが乗っている）の立体の塗り分けを考えます．
以下は展開図

6色を使って塗り分けます．
5回回転軸は6本ありますが，それぞれを地球の地軸とすると，それぞれの赤道に相当する大円に配置される1色が保存され，残りの5色が順番に置換されます．3回回転軸は10本ありますが，それぞれ2組の3色置換になります．

実は，正20面体（あるいは，正12面体）群の位数（対称操作の総数）は60です（ユニット数に等しい）．
ーーーーー
■平面
「大川組子」（昔，さなさんブログから教えていただきました）という伝統工芸があります．シンプルで精緻な組子で感動します．ななつ星の写真をご参照ください．

これらの組子はどちらも三角の格子でできています．ただし，どちらの組子も格子の中身に，対称性は同じだが異なるモチーフが2種類（あるいは3種類）あり，単純ではない面白い図案になっています．
さて今日は，この組子とユニット折り紙の関係についてです．

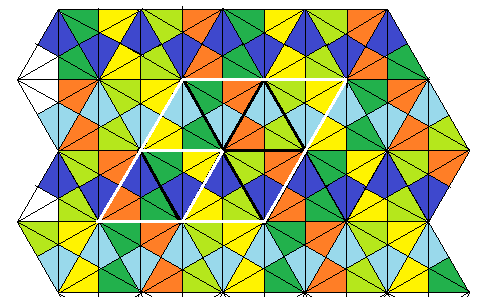
ユニット折り紙で作る多面体の場合と異なり，平面ですので正三角形が頂点で6つ集まっています．
そして正三角形の格子の上にピラミッドが乗っています．
図はユニット折り紙でこれを作り真上から見たものです．
6回軸の色置換を完全にするために，この図では６色使いました．
（地図の塗り分けで，4色問題というのがありましたね．長い間未解決の難問でしたが今は証明されています．この図の場合は，実は3色あれば塗り分けられます．一色の周りは4辺で，皆頂点で接続していますから）

そして，これは壁紙模様の平面群の一つで6回対称です．
色置換の対称性も完全にするには6色で塗り分ける必要があります．
色の区別ができる場合の単位胞タイルは大きな白い4辺形，
色の区別ができない場合の単位胞は小さな白い4辺形です．