
球体の2つの対称類
幾何学を学んだ人は、証明しなくても明らかなことを証明しなければならないときに、最大の困難を経験したことでしょう。球体の対称性についても同様です。球体は最も単純な図形の一つですが、最も複雑な対称性を持っています。連続等方な物質、すなわち、すべての方向が等価な物質でできた普通の球は、球の中心を通るあらゆる直径に沿って無限位数の対称軸を持っています。[無限位数というのは,微小角度の回転でも対称性を保つ回転対称軸です]
これらの軸をのせる対称面が無数にあります。対称心は、球の中心と一致します。さらに、これらすべての対称要素が存在する結果として、球は、単純回転軸および回映軸の両者を含む無限集合を含んでいます。球の対称要素の完全な集合を得るためには、生成要素(生成元)として、任意の角度の2つの無限軸と1つの対称面を採用するだけで十分です:∞/∞・m
球体の中心はその特異点です。球の内部または表面上の任意の点は、中心から同じ距離にある等価な点の無限集合をなしています。有限群では、群の位数(群内の異なる対称変換の数)を、等価点の数と点の多重度の積として定義しました。無限群の場合に対応する量を決定するには、群論や集合論からのより複雑な方法を用いなければなりません。
無限群では、位数の概念はべき乗の概念に置き換えられます。無限群Gを無限部分群Hに対して一連の剰余類で展開すると、
![]()
Gの位数はHの位数にsをかけたものになります。また、群を余因子の積で表すと、その位数(べき乗)は余因子の位数の積に等しい。

これらの極限群の位数は、それぞれ、2∞,2∞,2∞,4∞,2∞^3 です。
ここで、∞は,群∞を示す円錐の円形断面を形成する等価な点の一次元連続体の位数です。この断面のすべての点は、∞群では1倍ですが、∞mm群では2倍になります。なぜなら、対称面mがこれらの点のすべてを通過するからです。
同様に、円柱の円形断面の中央部の点は、m, 2, mm2群に属する変換の作用を受けてもそれぞれの位置が維持されるので、∞/m, ∞22群では2倍、∞/mmm群では4倍になることがわかる。∞∞群と∞∞m群では、等価な点が∞^2の2次元の球形の連続体を形成しており、これらの点の数∞とそれらの多重度である2∞を掛け合わせて、現在の関心事である∞∞群の位数を決定している。∞∞群の位数=∞^2・∞ =∞^3, ∞∞m群の位数=∞^2・2∞=2∞^3
対称形のクラスごとに、非常に多くの異なるタイプの図形が無限に存在することがすでにわかっています。球面対称はこの点では例外で、クラス ∞/∞・m は球、より正確には、任意の半径の同心円球のシステムにのみ適用されます。
立方体の場合、正多面体の対称クラスの数が3から7に増えたのは、幾何学的等価性(合同、鏡像の存在)に加えて、図形面の物理的な等価性を考慮したからである。類似していることから、球体、すなわち、すべての方向に等しい半径を持つ図形は、いくつかの対称クラスを持つことが予想される。球の対称性を考えるために、3つの球の表面にコンマの形をした非対称なウロコがついていると想像してみよう。
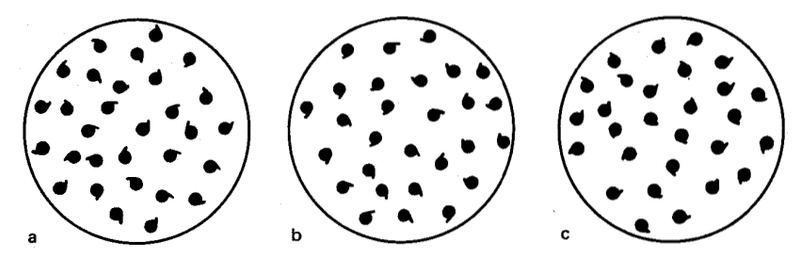
ウロコの分布は任意であるが、密度は均一である。1つ目の球の表面には右回りと左回りのコンマが同じ数だけあり、2つ目の球の目盛りは右回りのコンマだけで構成され、3つ目の球の目盛りは左回りのコンマだけで構成されています。1つ目の球を手に取り、まず左に回転させ、次に右に回転させると、右回転と左回転の摩擦力に違いはありません。どちらの場合も、手に著しい傷をつける目盛りの数が等しいからです。2番目と3番目の球体では状況が異なります。これらの球体では、時計回りと反時計回りの回転に伴う摩擦が異なるからである。読者は、我々の鱗のあるボールは真の球体とは見なされないので、ボールに当てはまることが理想的な球体にも当てはまるとは限らないと反論するかもしれない。これに対して私たちは、「本当の」球は、ある有限の精度以上には理想的な法則を満たさない物質的な球でしかないと答えます。さらに、理想的な球であっても、鱗が無限小さければ、鱗状になり得ます。
また、対称面のない球体の例として、透明なガラス球に有機物(砂糖など)の水溶液を入れると、光線の偏光面が左右に回転します。このような球体に偏光した光を通すと、溶解した物質の性質に応じて偏光面が右回り、左回りに回転する。
このように、理論的にも実際にも、球の対称性には2つのクラスが存在することがわかります。最初のクラス(∞/∞・m)では、無限の対称面、無限位数の対称軸、および対称心がありますが、2番目のクラス(∞/∞)では、対称面と対称心はありません。軸以外の対称要素が存在しない他のすべての対称クラスと同様に、球対称の第2クラス(∞/∞)は、2つの対掌体があります。右手および左手の球は、∞/∞対称性を持つ図形です。すべての球体の半径は等しいので、すべての球体は等方的であります。
これらの異なる対称性を持つ球体は、自然界ではいわゆる球晶の形で見られる。球晶の発生と成長は、様々な物質を人工的に調製したものを、対物ガラスとカバーガラスの間に少量ずつ溶かして、顕微鏡で簡単に観察することができる。試料を冷やすと、しばしば球晶が現れる。
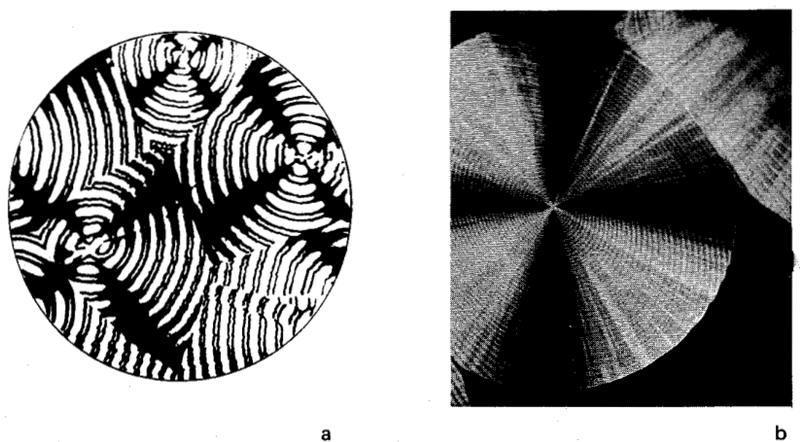
この実験は、特に硫黄でうまくいきます。球晶または球状硫黄結晶は、細い(おそらく分子レベルで細い)放射状のフィラメントで構成されています。球晶を偏光で観察し、クロスニコルで観察すると、常に黒い十字が見えます(図68参照)。顕微鏡のステージ・テーブルを回転させても静止している。この光学的現象は、球晶が放射状の構造を持っていることを証明するものです。球状結晶の中には、繊維がねじれているものがあり、これを偏光で観察すると、干渉色の同心円が交互に現れる。
ねじれの性質によって、右巻きの球晶と左巻きの球晶を明確に区別することができる。捻じれていない繊維の球状物質は、通常の球の対称性を持っている。
この記事が気に入ったらサポートをしてみませんか?
