No.068 統計学のお勉強 1標本 母比率の検定

1.今回の目的

統計検定2級の勉強をしていますが、文系出身の私にはかなり難しいです。
過去問をパターン化して、取れる問題を確実にゲットしたいといことで、今回は母比率の検定について2018年-2021年6月の過去問をまとめてみました。
統計検定2級公式問題集2018-2022年(日本統計学会編)を参考にpythonで問題を解いてみます。
この過去問集では、2018年6月、2018年11月、2019年6月、 2019年11月、2021年6月と計5回の検定試験の問題が網羅されています。
調べてみたところ、1標本の母比率の検定は毎回1問出題されています。

著作権の関係もあるので、問題の概要はさらっとまとめますが、以下のような問題です。

1. 2021年6月_問17(1):  500回の画びょう投げ→284回表  95％信頼区間は?

2. 2019年11月_問13:  100人に出口調査 Aに投票は54人  95%信頼区間は？

3. 2019年6月_問14:  300匹の魚に目印してリリース後、再度池から魚を200匹捕獲すると20匹に目印がついていた。95%信頼区間は?

4. 2018年11月_問12:  アンケート回答者1338人中 ほぼ毎日利用する人の割合は2.0%.  95%信頼区間は?

5. 2018年6月_問11(1):  総務省の調査によると、北海道の野球の行動者率は7.1%, 標本サイズは4663人。 95%信頼区間は?

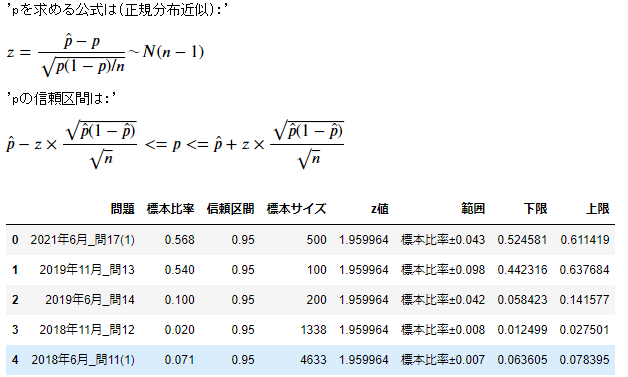
この問題において、計算の前提として必要なのは、標本比率と信頼区間と標本サイズです。それを下記の式に当てはめます。なお、過去5回ともに95％区間で問題が出ていますので、思い切ってz=1.96という値を暗記してしまうのも良いと思います。

あとは、√(標本比率 x (1-標本比率) / 標本サイズ)をかけて、標本比率からの±すれば算出されます。pythonで一気にといて、後は自力で計算もできるように練習します。

import numpy as np
import pandas as pd
from IPython.display import display
from IPython.display import Math

df=pd.DataFrame({'問題':['2021年6月_問17(1)','2019年11月_問13','2019年6月_問14','2018年11月_問12','2018年6月_問11(1)'],
    '標本比率':[284/500,54/100,20/200,0.02,0.071],
    '信頼区間':[0.95,0.95,0.95,0.95,0.95],       
    '標本サイズ': [500,100, 200,1338,4633]})
df

df['z値']=stats.norm.ppf(loc = 0, scale = 1, q = (1-df['信頼区間'])/2)*-1
df['範囲']='標本比率±'+(np.round(df['z値'] * np.sqrt(df['標本比率']*(1-df['標本比率'])/df['標本サイズ']),3)).astype(str)
df['下限'] = df['標本比率'] - df['z値'] * np.sqrt(df['標本比率']*(1-df['標本比率'])/df['標本サイズ'])
df['上限'] = df['標本比率'] + df['z値'] * np.sqrt(df['標本比率']*(1-df['標本比率'])/df['標本サイズ'])

display('pを求める公式は(正規分布近似):',Math(r'{z=\frac{\hat{p}-p}{\sqrt{p(1-p)/n}}}～N(n-1)'))
display('pの信頼区間は:',Math(r'\hat{p}-z\times\frac{\sqrt{\hat{p}(1-\hat{p})}}{\sqrt{n}}<=p<=\hat{p}+z\times\frac{\sqrt{\hat{p}(1-\hat{p})}}{\sqrt{n}}'))
df

以上です。