小角X線散乱（SAXS）（9）- 【演習】Zimmプロット

Zimmプロットの式を導き出す練習問題です。

【演習】Zimmプロット

---

ランダムに配向している粒子において、散乱ベクトル$${h}$$が十分小さい領域$${(h\ll 1/R_G)}$$では、一般的に次のZimmプロットが成り立つことを示せ[1]：

$$
P(h)^{-1}=1+\dfrac{R_G^2}{3}h^2+\cdots,           \;\;\;\;\;\; (1)
$$

$${P(h)}$$：散乱関数[1]、$${h}$$：散乱ベクトル[1]の大きさ、$${R_G}$$：回転半径

ただし、回転半径$${R_G}$$は、離散点の場合は、

$$
R_G^2 = \dfrac{\sum_k f_k (\boldsymbol{r}_k - \boldsymbol{r}_G )^2}{\sum_k f_k}　\;\;\;\;\;\; (2)
$$

で定義され、連続体の場合は、

$$
R_G^2 = \dfrac{\int_V \rho(\boldsymbol{r})(\boldsymbol{r} - \boldsymbol{r}_G )^2 \mathrm{d}\boldsymbol{r}}{\int_V  \rho(\boldsymbol{r}) \mathrm{d}\boldsymbol{r}} \;\;\;\;\;\; (3)
$$

で定義されるものとする。

$${\boldsymbol{r}_k}$$：散乱点$${k}$$の位置ベクトル、$${f_k}$$：散乱点$${k}$$での電子の個数、$${\boldsymbol{r}_G}$$：電子の分布の重心、$${\rho(\boldsymbol{r})}$$：位置ベクトル$${\boldsymbol{r}}$$での電子密度、$${V}$$：粒子の領域

図1 点Gは電子の分布の重心。点Pは任意の散乱点。

なお、重心$${\boldsymbol{r}_G}$$は、次式で定義される：

$$
\boldsymbol{r}_G = \dfrac{\sum_k f_k \boldsymbol{r}_k}{\sum_k f_k} = \dfrac{\int_V \rho(\boldsymbol{r}) \boldsymbol{r} \mathrm{d} \boldsymbol{r}}{\int_V \rho(\boldsymbol{r}) \mathrm{d} \boldsymbol{r}}
$$

---

【解説】
離散点の場合：
ランダムに配向している粒子では、散乱強度$${I(h)}$$について次のDebyeの散乱式が成り立ちます[1]：

$$
I(h)=A_e^2\displaystyle\sum_{j}\displaystyle\sum_{k}f_jf_k\dfrac{\sin{hr_{jk}}}{hr_{jk}}
$$

$$
r_{jk} =|\boldsymbol{r}_{jk}|\\\boldsymbol{r}_{jk} =\boldsymbol{r}_k - \boldsymbol{r}_j
$$

ここで、

$$
\displaystyle \frac{\sin x}{x} =\displaystyle \sum_{n=0}^\infty (-1)^n\frac{x^{2n}}{(2n+1)!} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} +- \cdots \;\;\;\; [|x|<\infty]
$$

を利用すれば、

$$
I(h)=A_e^2\displaystyle\sum_{j}\displaystyle\sum_{k}f_jf_k \big (1-\dfrac{r_{jk}^2}{6}h^2 + \cdots \big )\\ =A_e^2 \Big (\displaystyle\sum_{j}\displaystyle\sum_{k}f_jf_k -\dfrac{\sum_{j}\sum_{k}f_jf_k r_{jk}^2}{6} h^2 + \cdots \Big) \;\;\;\;\;\;\; (4)
$$

式を変形します：

$$
r_{jk}^2 = (\boldsymbol{r}_k - \boldsymbol{r}_j)^2=\{(\boldsymbol{r}_k - \boldsymbol{r}_G) - (\boldsymbol{r}_j - \boldsymbol{r}_G) \}^2 =\\ = (\boldsymbol{r}_k - \boldsymbol{r}_G)^2 + (\boldsymbol{r}_j - \boldsymbol{r}_G)^2 - 2 (\boldsymbol{r}_k - \boldsymbol{r}_G) \cdot (\boldsymbol{r}_j - \boldsymbol{r}_G)
$$

よって、

$$
\sum_{j}\sum_{k}f_jf_k r_{jk}^2 = \\ =\sum_{j}\sum_{k}f_jf_k (\boldsymbol{r}_k - \boldsymbol{r}_G)^2 + \sum_{j}\sum_{k}f_jf_k (\boldsymbol{r}_j - \boldsymbol{r}_G)^2 \\ - 2 \sum_{j}\sum_{k}f_jf_k (\boldsymbol{r}_k - \boldsymbol{r}_G) \cdot (\boldsymbol{r}_j - \boldsymbol{r}_G)\\ = \sum_jf_j\sum_k f_k (\boldsymbol{r}_k - \boldsymbol{r}_G)^2 + \sum_k f_k \sum_j f_j (\boldsymbol{r}_j - \boldsymbol{r}_G)^2 \\ - 2\sum_j f_j (\boldsymbol{r}_j - \boldsymbol{r}_G) \cdot \sum_k f_k (\boldsymbol{r}_k - \boldsymbol{r}_G) \;\;\;\;\;\; (5)
$$

ところで、重心の定義から、

$$
\sum_j f_j (\boldsymbol{r}_j - \boldsymbol{r}_G) = \boldsymbol{0} \;\;\;\;\;\; (6)
$$

になるので、

$$
\displaystyle \sum_{j}\sum_{k}f_jf_k r_{jk}^2 = 2\Big(\sum_k f_k \Big) \sum_k f_k (\boldsymbol{r}_k - \boldsymbol{r}_G)^2  \;\;\;\;\;\; (7)
$$

これを式(4)に代入し、$${R_G}$$の定義式(2)を考慮すると、

$$
I(h)=A_e^2 \Big (\displaystyle\sum_{j}\displaystyle\sum_{k}f_jf_k - \dfrac{\Big(\sum_k f_k \Big) \sum_k f_k (\boldsymbol{r}_k - \boldsymbol{r}_G)^2}{3}h^2 + \cdots \Big) =\\ = A_e^2 \Big (\displaystyle \sum_k f_k \Big )^2 \Big (1 - \dfrac{\sum_k f_k (\boldsymbol{r}_k - \boldsymbol{r}_G)^2}{3\sum_k f_k} h^2+ \cdots \Big )=\\ = A_e^2 \Big (\displaystyle \sum_k f_k \Big )^2 \Big (1 - \dfrac{R_G^2}{3} h^2 + \cdots \Big ) \;\;\;\;\;\; (8)
$$

ここで、$${\sum_j \sum_k f_j f_k = (\sum_k f_k)^2}$$を用いました。

$$
I(0) = \displaystyle \lim_{h \to 0} I(h) = A_e^2 \Big (\displaystyle \sum_k f_k \Big )^2　\;\;\;\;\;\; (9)
$$

だから、散乱関数$${P(h)(=I(h)/I(0))}$$は、$${h}$$の2次までとると、

$$
P(h) = 1 - \dfrac{R_G^2}{3} h^2 +- \cdots
$$

よって、

$$
\dfrac{1}{P(h)} = 1 + \dfrac{R_G^2}{3} h^2 +- \cdots
$$

ここで、べき級数、

$$
\displaystyle \frac{1}{1-x} = \displaystyle \sum_{n=0}^\infty x^n = 1+x+x^2+x^3+ \cdots \; [|x|< 1]
$$

を使いました。
（離散点の場合終）

連続体の場合：
Debyeの散乱式は[1]、

$$
I(h) = A_e^2 \displaystyle \int_V \int_V \rho(\boldsymbol{r}) \rho(\boldsymbol{r}') \dfrac{\sin{h |\boldsymbol{r}-\boldsymbol{r}'|}}{h|\boldsymbol{r}-\boldsymbol{r}'|} \mathrm{d}\boldsymbol{r} \mathrm{d}\boldsymbol{r}'
$$

式(4)に相当する式は、

$$
I(h) = A_e^2 \Big ( \displaystyle \int_V \int_V \rho(\boldsymbol{r}) \rho(\boldsymbol{r}') \mathrm{d}\boldsymbol{r} \mathrm{d}\boldsymbol{r}' - \frac{h^2}{6}  \displaystyle \int_V \int_V \rho(\boldsymbol{r}) \rho(\boldsymbol{r}') (\boldsymbol{r} - \boldsymbol{r}')^2 \mathrm{d}\boldsymbol{r} \mathrm{d}\boldsymbol{r}' + \cdots \Big )
$$

式(5)に相当する式は、

$$
\displaystyle \int_V \int_V \rho(\boldsymbol{r}) \rho(\boldsymbol{r}') (\boldsymbol{r} - \boldsymbol{r}')^2 \mathrm{d}\boldsymbol{r} \mathrm{d}\boldsymbol{r}' = \\ = \displaystyle \int_V \rho(\boldsymbol{r}')\mathrm{d}\boldsymbol{r}' \int_V \rho(\boldsymbol{r})(\boldsymbol{r}-\boldsymbol{r}_G)^2 \mathrm{d}\boldsymbol{r} + \displaystyle \int_V \rho(\boldsymbol{r})\mathrm{d}\boldsymbol{r} \int_V \rho(\boldsymbol{r}')(\boldsymbol{r}'-\boldsymbol{r}_G)^2 \mathrm{d}\boldsymbol{r}' \\ - 2\int_V \rho(\boldsymbol{r})(\boldsymbol{r}-\boldsymbol{r}_G) \mathrm{d}\boldsymbol{r} \cdot \int_V \rho(\boldsymbol{r}')(\boldsymbol{r}'-\boldsymbol{r}_G) \mathrm{d}\boldsymbol{r}'
$$

重心の定義から、式(6)に相当して、

$$
\displaystyle \int_V \rho(\boldsymbol{r})(\boldsymbol{r}-\boldsymbol{r}_G) \mathrm{d}\boldsymbol{r} = \boldsymbol 0
$$

式(7)に相当して、

$$
\displaystyle \int_V \int_V \rho(\boldsymbol{r}) \rho(\boldsymbol{r}') (\boldsymbol{r} - \boldsymbol{r}')^2 \mathrm{d}\boldsymbol{r} \mathrm{d}\boldsymbol{r}' = 2 \int_V \rho(\boldsymbol{r}')\mathrm{d}\boldsymbol{r}' \int_V \rho(\boldsymbol{r})(\boldsymbol{r}-\boldsymbol{r}_G)^2 \mathrm{d}\boldsymbol{r}
$$

結局、式(8)に相当して、

$$
I(h) = A_e^2 \Big ( \displaystyle \int_V \rho(\boldsymbol{r}) \mathrm{d} \boldsymbol{r} \Big )^2 \Big (1 - \dfrac{\int_V \rho(\boldsymbol{r})(\boldsymbol{r} - \boldsymbol{r}_G )^2\mathrm{d}\boldsymbol{r}}{3 \int_V \rho(\boldsymbol{r}) \mathrm{d}\boldsymbol{r}} h^2+ \cdots \Big )=\\ =A_e^2 \Big ( \displaystyle \int_V \rho(\boldsymbol{r}) \mathrm{d} \boldsymbol{r} \Big )^2 \Big (1 - \dfrac{R_G^2}{3 } h^2+ \cdots \Big )
$$

ここでも、回転半径$${R_G}$$の定義式(3)を用いました。また、

$$
\displaystyle \int_V \int_V \rho(\boldsymbol{r}) \rho(\boldsymbol{r}') \mathrm{d}\boldsymbol{r} \mathrm{d}\boldsymbol{r}' = \displaystyle \int_V \rho(\boldsymbol{r})\mathrm{d}\boldsymbol{r} \int_V\rho(\boldsymbol{r}')  \mathrm{d}\boldsymbol{r}' =\Big( \displaystyle \int_V \rho(\boldsymbol{r})\mathrm{d}\boldsymbol{r} \Big )^2
$$

を用いました。式(9)に相当して、

$$
I(0) = \displaystyle \lim_{h \to 0} I(h) = A_e^2 \Big (\displaystyle \int_V \rho(\boldsymbol{r}) \mathrm{d}\boldsymbol{r} \Big )^2
$$

となります。これ以降の式は離散点の場合と同じです。
（連続体の場合終）

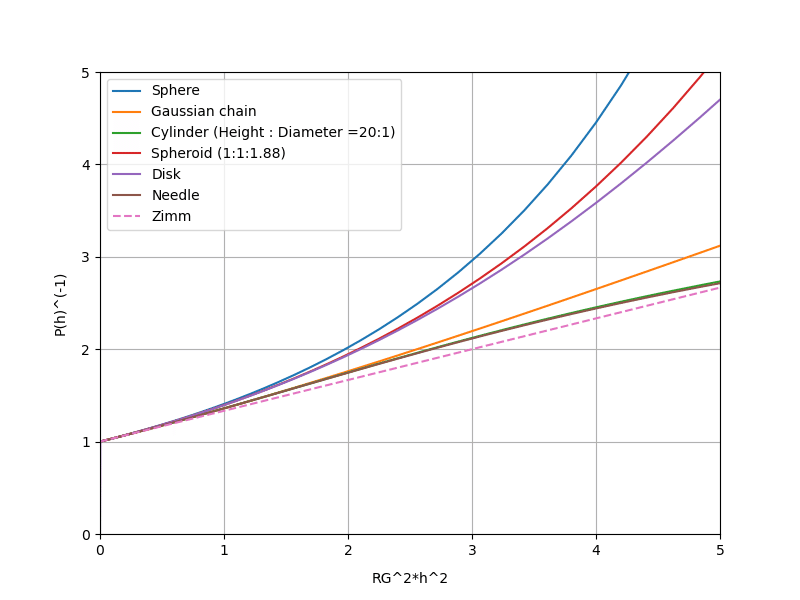
下図は典型的な形状の散乱関数$${P(h)}$$をZimmプロットしたものです[1]：

図2 簡単な形状のZimmプロット。初期勾配から回転半径RGが求められます。縦軸は散乱関数P(h)の逆数、横軸は波数ベクトルの2乗で、回転半径RGで規格化されています。球（Sphere)、ガウス鎖（Gaussian chain）、円柱（Cylinder）、回転楕円体（Spheroid）、無限に薄い円板（Disk）、無限に細い棒（Needle）。破線（Zimm）は傾き1/3の直線。Pythonで計算しました。

文献

[1] 小角X線散乱（SAXS）（1） - 基本的なこと（note記事）

---

【免責事項】本記事は単なるメモとして書かれたもので、その正確性を必ずしも保証するものではありません。本記事によって生じたトラブル、損失、又は損害に対して一切責任を負いません。また、著者が所属する組織とは関係ありません。誤りがあればご指摘ください。クレームはご遠慮ください。