2重N足振り子の運動方程式

こんにちは、えむしーじじょうのShikiです。

今回は変わった振り子の運動方程式のお話。N重振り子の方程式のときと同様に、導出の過程はpdfで清書しましたので、興味ある方はダウンロードしてみて下さい。

2重N足振り子の運動方程式.pdf

186744 Bytes

ファイルダウンロードについて

ダウンロード

まえがき

N重振り子で面白い初期条件は無いかと思案していたら、ペンデュラムウェーブという面白い振り子の存在を発見しました。

これはこれで面白いのですが、このペンデュラムウェーブのような複数の振り子を振り子に付けてみたらどうなるだろうか、ということに興味を引かれてしまいました。

さっそく、運動方程式を求めてみるとすぐに式の傾向が見えきて、さくっとN次まで求めることができました。そうして、texで資料にまとめて、シミュレーション動画も作り一区切りが付いたのでnoteで紹介することにいたしました。

ちなみに2重N足振り子という名前ですが、調べた限りでは呼び名が分からなかったため、私が名付けています。もし、先行研究などで既に名前が付いているのであればご一報下さい。

2重振り子

まずはここから始まります。2重N足振り子で言うところの2重1足振り子になります。N重振り子の記事で既にやっているので再掲となります。前記事同様に変数の定義や導出の過程は「2重N足振り子の運動方程式.pdf」の1章をご覧頂くとして、結果だけを示すと運動方程式は次のようになり

角度に関する加速度は次のようになります。

そしてお次は2重2足振り子です。

2重2足振り子

2重2足振り子は人の足をモデル化する例として求められている記事がありました。ネーミングもそれに因んでいます。私自身は初めて求める運動方程式だったのですが、なかなか奇麗な形に収まりました。演習問題にしても良いレベルです。変数の定義や導出の過程は「2重N足振り子の運動方程式.pdf」の2章をご覧下さい。運動方程式は次のようになり

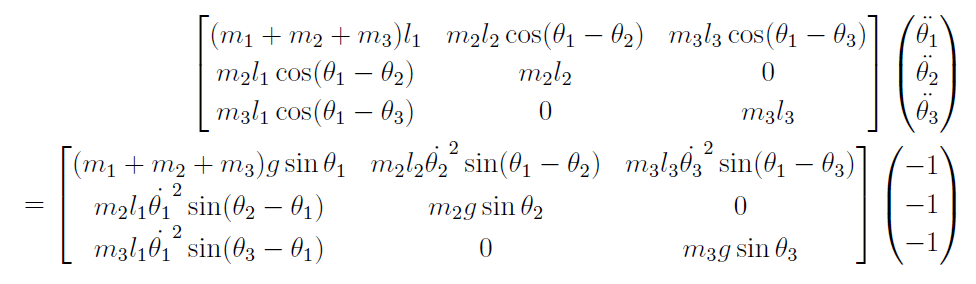
角度に関する加速度は次のようになります。

式や動画から分かることですが2重2足振り子は質点m2と質点m3は質点m1を介して力の伝達しています。そのため、片方が最下点・速度0の初期値でも、もう一方が動いていればm1を介して動き出します。そして、当然ですが、2重振り子の延長なので、この振り子もカオスになっています。

そして、この式を眺めると既に傾向が見えてきたので、2重3足振り子を求めることなく一気にN足に手を出しました。

2重N足振り子

数をいくら増やしたところで所詮は質点m1と繋がっているだけなので、恐るるに足らず。2重2足振り子の導出過程をiに変えてやる程度の労力で求めることができます。詳しい変数の定義や導出の過程は「2重N足振り子の運動方程式.pdf」の3章をご覧下さい。運動方程式と加速度は次のようになります。大きい括弧を使った行列で表す方が、分かりが良いかもと思いつつ、要素での表現にしてみました。

このA,Bの要素をpythonで書く場合は以下のようにして定義できます。

for i in range(n):
   for j in range(n):
       if i == 0 and j == 0:
           for k in range(n):
               A[i][j] += m[k]
               B[i][j] += m[k]
       elif i == 0 or j == 0 or i == j:
           A[i][j] += m[max(i,j)]
           B[i][j] += m[max(i,j)]
           
       if i == j:
           A[i][j] *= l[j]
           B[i][j] *= g * np.sin(x[i])
       elif i == 0 or j == 0:
           A[i][j] *= l[j]*np.cos(x[i]-x[j])
           B[i][j] *= l[j]*v[j]**2*np.sin(x[i]-x[j])

また、計算途中でm,g,lが一定である場合(ほとんどそうだと思いますが…)は積分の計算前に定数としてまとめて計算すると高速化できます。numpyの行列計算の性質を利用するとさらに高速化できますが、副作用でコードが複雑化してくるので注意が必要です。

ということで、シミュレーション結果のご紹介。

2重32足振り子辺りでサイエンスアートとして楽しめるようになってきました。最後に示している2重1024足振り子はどこまで増やすことができるか、というチャレンジ精神で計算したものになります(15時間くらいかかったので二度とやりたくないですが…)。美しい仕上がりになったので(PCが)苦労した甲斐がありました。

N重振り子の場合は計算負荷の問題だけでなく、Nを増やすと計算誤差によってエネルギーが保存されない問題がありました。ところが2重N足振り子は系が単純なため、Nをどこまで増やしても積分が安定しエネルギーが保存されます。だから、処理速度が許す限りどこまでも増やすことができます。

「簡単、軽い、美しい」そんな2重N足振り子を紹介いたしました。

終わり。