
三角山パズルに使っている立体の正方形に注目
三角山パズルでは56個の特別な立体を使っています。
立体の名前は切稜立方体といって立方体の12個の辺(稜)を45°で切り取ってできる立体です。切り取ると12個の面が増えますので立方体の6面に加えて18面体になります。ごく浅く切り取ると面取りされた立方体ですし、立方体の面がなくなるまで深く切り取ると菱形12面体になります。切り取る面の対面との距離を立方体の辺の長さに合わせると18の面が全て球に接する「内接球を持つ切稜立方体」になります。三角山パズルに使っているのがその立体です。
立方体の切り残された6面が正方形です。一辺の長さは外形の八角形の一辺の長さと同じです。

元の立方体の一辺の長さを1とした時に、正方形の一辺の長さはいくつでしょうか? 考えるのが嫌な時にはFusion360でモデルを作って寸法を調べたりします。立方体の一辺が30mmの時は12.426mmでした。一辺の長さが1の時には、30mmで割って0.4142になります。

正方形ABCDと八角形EFGHIJKLと正方形の中心をOとします。正方形の一辺の長さAB=1とします。LEは正八角形の一辺です。正方形の一辺ABの中点をM、正八角形の一辺LEの中点をN、として、OM=ON=1/2です。OAは45°の直角三角形AMOの斜辺なので√2/2 です。AN = AO-NO = √2/2 - 1/2です。
AN = LN = NEなので、八角形の一辺LEは √2 - 1 となります。
なので、立方体の切り残された正方形の一辺の長さは(√2 - 1) = 0.4142…
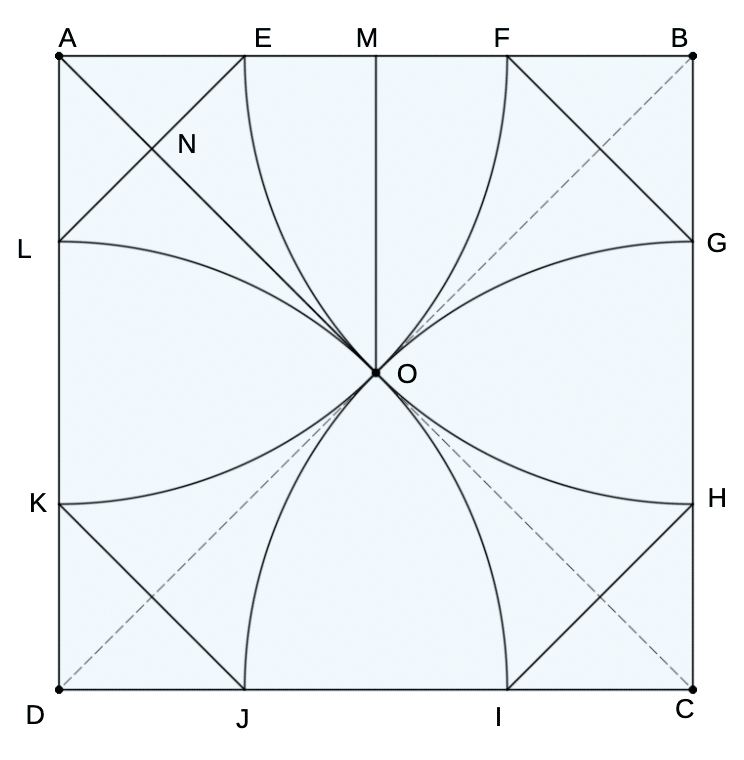
正方形から定規とコンパスで正八角形を描く時には頂点から中心を通る円弧を描いて辺と交わる点を正八角形の頂点とすれば良いということも昔から知られているらしい。
EF = AB - AE - FB
AE = FB = 1 - √2/2
EF 1 - (1 - √2/2) x 2 = √2 - 1
この記事が気に入ったらサポートをしてみませんか?
