Co-Localization 4　3.定量分析

３．定量分析

　本章（３．定量分析）では、共局在の定量に用いる指標・検定法について解説します。共局在の定量方法は大別して２つあります。定量を、画像のピクセル単位 (pixel by pixel)でおこなうのか、それとも標的分子のクラスター単位 (cluster by cluster)でおこなうのかの２つです。ピクセル単位の定量は標的分子の局在パターンに関係なくどんな画像にも適用できます。一方、クラスター単位の定量は、標的分子が輝点状・粒子状の局在パターンを示すときにのみ用いることができます。ピクセル単位・クラスター単位いずれも定量に用いる指標 (index)が複数あります。いずれの指標も長所・短所があり、指標の不適切な選択は誤った解釈へと繋がります。研究者は指標の長所・短所をしっかりと理解する必要があります。

ピクセル単位での定量

　ピクセル単位 (pixel by pixel)での定量は、統計学の相関係数の定量とよく似ています。相関係数の定量と同じように、複数の指標があり、各指標で長所・短所が異なります。そのため、画像のSNや研究目的にふさわしい適切な指標を選択する必要があります。研究者が最適な指標を選択できるように、各指標の長所・短所を解説しました。選択の大きな基準として、「蛍光分子のシグナルに外れ値・異常値があるか」と「バックグランド値、Threshold値を正確に決定できるか」の２つが挙げられます。まずは、この2つの基準を判定するために、2色の蛍光シグナルの散布図を作成し、データの分布を可視化すべきです。シグナルに外れ値・異常値がなければPearson係数が第一候補となります。外れ値・異常値があった場合、Spearman係数・Kendall係数・ICQ・Manders Correlation係数といった他の選択肢が候補となります。ただし、上記2つの基準以外にも選択の基準はあるのでそれぞれの指標をしっかりと理解することが大事です。さらに、算出された指標の値は、統計学的な有意性を検定する必要があります。検定の方法は、2色の画像の一方の画像を、バラバラにするか (randomization)、ずらすか (translation)で2つに大別されます。これについても解説します。

「Pearson係数 (PCC)」

　Pearson係数 (PCC)とは、統計学のPearsonの積率相関係数、つまり一般的に使われている相関係数のことです。-１から１の値を取り、値が負の場合は２分子の局在に負の相関が、０の場合は無相関、正の場合は正の相関があります。Pearson係数 (PCC)の長所は、バックグラウンドの蛍光の影響を受けないことです（図１）。蛍光輝度の絶対値ではなく、平均値からの差（偏差）、つまり相対値を使って算出しているからです。このため、SNが悪くバックグラウンドを正確に減算できない画像の定量をすることが可能です。また別の長所として、パラメトリックな定量であるため、標本集団が正規分布であるならば、定量した値の正確性が高いです。

　一方、PCCの短所は3つあります。１つ目は外れ値やノイズの影響を受けやすいことです。標本集団が正規分布している（パラメトリック）という仮定に基づいているためです。例えば、ほとんどのピクセルで相関がなくても、非常に大きな蛍光強度を持つピクセルに相関があった場合、係数の値が大きくなり現実の共局在を反映した値ではなくなります（図２）。正規性検定や散布図作成といった方法で、標本集団が正規分布しているか、つまり、パラメトリックであるかを確認する必要があります。2つ目の短所は、係数の値から共局在のパターンを想像することが難しいことです。値が+1や-1に近い場合、解釈は容易ですが、係数の値が中間(-0.5～0.5)的な場合、2つの分子がどのように局在しているかが想像できません（図３）。3つ目は、各色（各分子）の個別の情報を含んでいないことです。個別の情報とは、たとえば赤色の分子のほとんどは緑色の分子と共局在しているが、逆に緑色の分子は一部が共局在しているだけで大部分は共局在していないといったことです。このため、これらPCCの短所を補う指標が開発されてきました（後述）。

「Spearman係数」

　Spearmanの順位相関係数のことです。外れ値の影響を受けやすいPearson係数の短所を克服した、ノンパラメトリックな指標です。計算方法はPearson係数と同じですが、Pearson係数のように蛍光強度の「値」ではなく、蛍光強度の「順位」を計算に用いています。蛍光強度の「順位」とは、各ピクセルの蛍光強度の「値」を、すべてのピクセルで順位付けし直したものです。つまり、データを比例尺度から間隔尺度へと変換し、正規化しています。正規化によって、データに外れ値が存在していても、外れ値の影響を受けずに定量することが可能です。Pearson係数と同様に、Spearman係数はバックグラウンドの影響を受けません。また、ノンパラメトリックな手法のため、標本集団の分布の形を問わないという点も長所です。一方、短所は、間隔尺度というノンパラメトリックな手法で定量しているため、パラメトリックなPearson係数に比べ正確性では劣ります。そのため、外れ値がない、正規分布つまりパラメトリックなデータではPearson係数を用いるべきです。

「Kendall係数」

　Kendallの順位相関係数のことです。Spearman係数と同様にPearson係数の短所を克服した、ノンパラメトリックな指標です。任意の２ピクセル間の蛍光輝度値の大小関係を使って相関を評価しています。具体的には、あるピクセルの蛍光輝度値が別のピクセルの値よりも、2色（ex. 赤と緑）とも大きいあるいは2色ともに小さい場合+1を、それ以外の場合 -1とします（データを比例尺度から順序尺度へと変換しています）。赤と緑色の間に正の相関があれば+1になる組が増えます。一方、相関が負であるならば -1になる組が増えます。すべてのピクセル間 (n(n-1)/2組) について計算を行い、その合計値で相関を評価しています。Pearson係数と同様に、-１から１の値を取ります。Kendall係数はSpearman係数とほぼ似たような値を示します。両者を使い分ける基準はなく、どちらを用いても差し支えがありません。長所・短所もSpearman係数の場合と同じになります。

「Intensity Correlation Quotient (ICQ)」

　Intensity Correlation Quotient (ICQ)は、Spearman・Kendall係数と同様にPearson係数の短所を克服した、ノンパラメトリックな指標です。求め方は、まず２色の偏差の積をピクセルごとに求めます（上の式参照）。偏差とは、平均値からの差のことで、偏差の積はProduct of the Difference from the Mean for each channel (PDM)と呼ばれます。PDMが正の値をとるピクセルは、各色の値が平均値よりも、共に多いあるいは共に少ない場合となり、正の相関があることを示しています。逆に、PDMが負の値をとるピクセルは、負の相関があることを示しています。そして、PDMが正の値をとるピクセルの割合を求めることで局在の相関性を評価しています。-0.5から0.5の値を取り、値が負の場合は２分子の局在に負の相関が、０の場合は無相関、正の場合は正の相関があります。データを比例尺度から名義尺度へと変換している以外は、Spearman・Kendall係数と似ています。そのため、長所・短所も両係数と同じです。両係数との違いに言及している文献がないため、両係数との使い分けの基準は不明です。

「Manders Correlation係数 (MCC)」

　Manders Correlation係数 (MCC)は、共局在している分子の割合を表しています。全ての分子のうち、何％が相手の分子と共局在しているかということです。指標値の意味がわかりやすいため、解釈が難しいPearson係数よりも扱いやすいという長所があります。計算式の分母は、全ピクセルの蛍光輝度の合計値です。計算式の分子は、相手の分子が存在しているピクセルのみの蛍光輝度の合計値です。MCCは、各分子（各色）ごとで別々に係数を算出しているため、各分子の個別情報がないPearson係数の短所も克服しています。

　MCCの注意すべき短所の１つ目として、２つの分子の相関関係を反映していない点が挙げられます。つまり、一緒にいるかどうかしか評価しておらず、「どのように」一緒にいるかは評価していないということです。共局在 (co-localization)とは、２つの要素を含んでいます。1つ目の要素は、単に空間的に同じ場所に存在する、オーバーラップしているかということです (co-occurrence)。２つ目の要素は、単なるオーバーラップだけではなく、そのオーバーラップに相関・比例関係があるかということです (correlation)。２つ目の要素 (correlation)まで評価するPearson係数 (PCC)に対し、MCCでは1つ目の要素 (co-occurrence)までしか評価していません。当然、共局在の相関性までは議論するときには、MCCを用いることはできません。

　２つ目の短所として、バックグラウンドの影響を受けやすいという点が挙げられます。MCCでは、相手分子の蛍光がわずかでもあれば、そのピクセルは共局在と判定しています。そのため、バックグラウンドの減算が不十分で、バックグラウンドの蛍光がわずかでも残っていた場合、相手分子が全く存在しなくても、そのピクセルは共局在と誤って判定されてしまいます。逆に、バックグラウンドの減算を過剰におこない、相手分子由来の蛍光の値まで減算した場合、相手分子が存在していても、そのピクセルは共局在していないと判定されることになります。MCCによる定量では、減算するバックグラウンドの値によって全く違った定量値が算出されるので特に注意が必要です。

　Manders Correlation係数 (MCC)とは別に、Manders Overlap係数 (MOC)という係数も存在します。混同しないように注意が必要です。MOCはPCCと似ていますが、デメリットが多いため使わないほうが無難です。

「normalized mean deviation product (nMDP)」

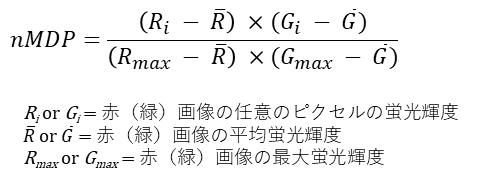
　normalized mean deviation product (nMDP)は、共局在の空間情報を表すことのできる唯一の指標です。他の指標は、すべてのピクセルを使って指標値を算出しているため、ピクセルごとの共局在の情報は平均化され、失われているからです。nMDPの求め方は、ICQと同様に、まず２色の偏差の積 (PDM)をピクセルごとに求めています。さらに、このPDMを偏差の最大値の積で平均化しています。この平均化によって、別の画像とのnMDP値の比較を可能にしています。nMDPの値は-1から1の値を取り、値が負の場合は２分子の局在に負の相関が、正の場合は正の相関があります。可視化の際には、負の値を寒色、正の値を暖色にすることで、共局在の空間的な解釈を容易にしています（下図）。nMDPは、PCCと同様に偏差を使っているので、バックグラウンドの蛍光があっても定量には影響を受けません。逆に、PCCと同様にパラメトリックな指標のため、外れ値・異常値の影響を受けます。また、nMDPはピクセルごとに算出されるため、特定のROIや画像全体の共局在の程度を１つの値として総括することはできません。総括する指標値として、nMDP値が正の値をとるピクセルの割合を、nMDPの提唱者F. Jaskolskiは提案しています (Icorr)。

https://sites.google.com/site/colocalizationcolormap/home

「threshold overlap score (TOS)」

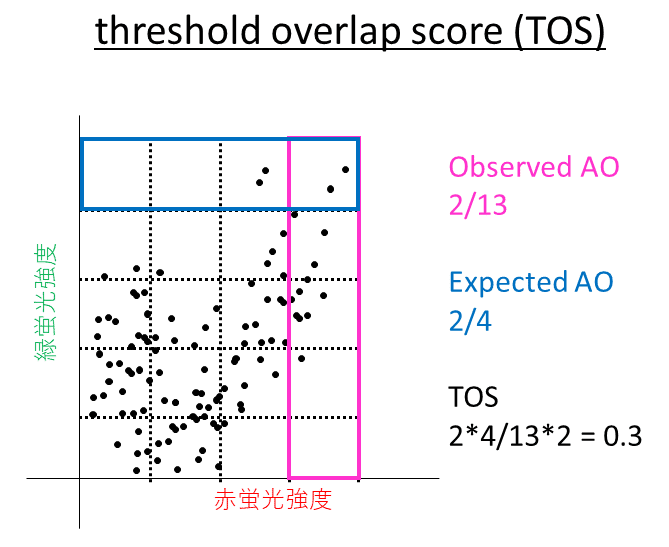
　threshold overlap score (TOS)は、不適切なThreshold設定・バックグラウンド減算によって、共局在の解釈を間違えてしまうことを防ぐために考案された指標です。TOSでは、Thresholdを任意に１つ設定するのではなく、機械的に複数設定します。そして、各Thresholdで定量をおこない、複数の結果を比較することで解釈の誤りを防いでいます。Thresholdは２色それぞれで設定しますので、定量結果は２次元行列のかたちで表されます。TOSの値は、データの存在確率の実測値と予測値の比で表されます（下図）。TOSの値は0以上の値をとり、1より大きければ共局在、1ならば偶然、1未満ならば”非”共局在とみなします。複数の結果の中から、最大のものをTOSmax、最小のものをTOSmin、Thresholdが最大のセルの値をTOShと定義しています。この3種類の指標の中から、画像状態・実験目的に応じた最適なものを選ぶことになります。TOSの短所としては、MCCと同様に、共局在の2つの要素、co-occurrenceとcorrelationのうち、1つ目のco-occurrenceまでしか評価していないことです。当然、共局在の相関性までは議論するときには、TOSを用いることはできません。

定量法まとめ

検定法

　定量した指標値が統計学的に有意かどうかを検定する必要があります。共局在の定量に用いた2色の画像の片方（e.x.赤）を「ランダム移動 (Randomization)」・「X方向水平移動 (X-translation)」・「XY方向水平移動 (XY-translation)」のいずれかで処理して、検定に使う画像を作成します。検定の方法は、検定に用いる画像の作成方法によって３つに分けられます。「ランダム移動 (Randomization)」によって作成した画像とは、定量に用いた画像 (オリジナル画像)の片方 (e.x. 赤)をPSF (point spread function)単位でバラバラにしてシャッフルした画像のことです。ランダム画像による検定は、以下の通りにおこないます。まず、ランダム画像 (e.x. 赤)とオリジナル画像 (e.x. 緑)とで共局在を定量します。この定量の値がオリジナル画像同士の値よりも低ければ、オリジナル画像の勝ちとします。ランダム画像の作成と定量を繰り返し、オリジナル画像の勝率を求めます。そして、オリジナル画像同士の勝率が９５％以上であれば、オリジナル画像同士の定量値は有意であると見まします。一方、「X方向水平移動 (X-translation)」・「XY方向水平移動 (XY-translation)」によって作成した画像とは、定量に用いた画像 (オリジナル画像)の片方 (e.x. 赤)を X方向あるいは XY方向に少しずつずらしていった画像のことです。水平移動画像による検定は、以下の通りにおこないます。まず、水平移動した画像 (e.x. 赤)とオリジナル画像 (e.x. 緑)とで共局在を定量します。移動距離を変えていき、定量を繰り返します。移動距離と定量値との関係をプロットし、局在に相関がなくなる距離を見出します。そして、局在が無相関となる距離以遠の水平移動画像だけの定量値のヒストグラムを作成します。このヒストグラムの９５％信頼区間外に、オリジナル画像同士の定量値が存在すれば、オリジナル画像同士の定量値は有意であるとみなします。
（引用F）

クラスター単位での定量

　標的分子の局在が輝点状・粒子状（クラスター）のパターンを示すときは、ピクセル単位ではなく、クラスター単位で共局在の定量をすべきです。輝点・粒子を単位として共局在を定量できるので、ピクセル単位での定量に比べ、より正確で、意義のある評価ができるためです。クラスター単位の定量方法は、３つのステップからなります。最初のステップで、標的分子の蛍光をクラスター単位に分離 (segmentation)します。ついで次のステップで、分離したクラスターの中心位置を求めます。そして最後のステップで、2色のクラスターの中心位置の距離を求めます。１つ目のステップの分離 (segmentation)は、それだけの説明でかなりのボリュームになってしまうため、別の機会に改めて解説します。次のステップで求める中心位置は、幾何中心 (geometric center)と質量中心 (center of mass)の2種類あります。幾何中心 (geometric center)とは、その図形に属する全ての点の算術平均の位置のことです。一方、質量中心 (center of mass)とは、蛍光輝度値を質量と見立て、その重力の合力の作用点の位置のことです。クラスター内で蛍光輝度分布が一様であれば、幾何中心と質量中心は同じ位置になります。研究の条件・目的に応じて、幾何中心と質量中心のどちらかを選択する必要があります。最後のステップで、最も近くにいる相手分子のクラスターとの中心位置間の距離を求めます。求めた距離を使って共局在を評価します。

　クラスター単位での共局在の評価の指標は２つあります。１つ目の指標は、単純にクラスター間の中心距離の平均値です (Nearest neighbor distance)。小さいほど近くに局在していることを示します。２つ目の指標は、相手クラスターと共局在しているクラスターの割合です (Center coincidence)。全クラスターのうち、何％が相手と一緒にいるかということです。一緒にいるかどうかは、クラスター間の中心距離がPSFよりも小さいかどうかで判定します。PSF (Point Spread Function)とは、日本語で点像分布関数と呼ばれています。PSFとは、無限に小さい「点」光源であっても、対物レンズといった光学系の特性によって、「広がり」をもって結像してしまうことです。通常は、広がりの半値全幅 (full width at half maximum, FWHM)で表現します。この広がりのため、PSFよりも近くにいる２点は、同じ空間に位置（共局在）しているとみなします。

参考文献・サイト

（引用F）
Steensel, B. van, E. P. van Binnendijk, C. D. Hornsby, H. T. van der Voort, Z. S. Krozowski, E. R. de Kloet, and R. van Driel. “Partial Colocalization of Glucocorticoid and Mineralocorticoid Receptors in Discrete Compartments in Nuclei of Rat Hippocampus Neurons.” Journal of Cell Science 109, no. 4 (April 1, 1996): 787–92.
Ramírez, O., A. García, R. Rojas, A. Couve, and S. Härtel. “Confined Displacement Algorithm Determines True and Random Colocalization in Fluorescence Microscopy.” Journal of Microscopy 239, no. 3 (2010): 173–83. https://doi.org/10.1111/j.1365-2818.2010.03369.x.
http://www.sussex.ac.uk/gdsc/intranet/pdfs/Colocalisation.pdf