SIRモデル・SZRモデルの数的解析　ゾンビの拡大を予測する

前回の記事はこちら

概要

SIRモデル・SZRモデルを方程式に落とし込み、数的解析を行った。解析によると、SIRモデルにおいては必ず感染は収束することがわかった。SZRモデルにおいては初動でゾンビを破壊しつくさない限り、必ず人類は滅亡する。

はじめに

SIRモデルとSZRモデルの記事では、様々にパラメータを代入してシミュレーションを行い、その結果を紹介した。しかしパラメータを設定し、その結果を見るためにいちいちシミュレーションをしていたのでは時間がかかって仕方がない。そこで今回は面倒なシミュレーションを省略し、結果を予測するための数的解析の手法を紹介する。

SIRモデルの数式化

まず、数的解析のためにSIRモデルを例にシミュレーションの数式化を行う。SIRモデルは次の図で説明されるものだった。Sが非感染者、Iが感染者、Rが除外者だ。

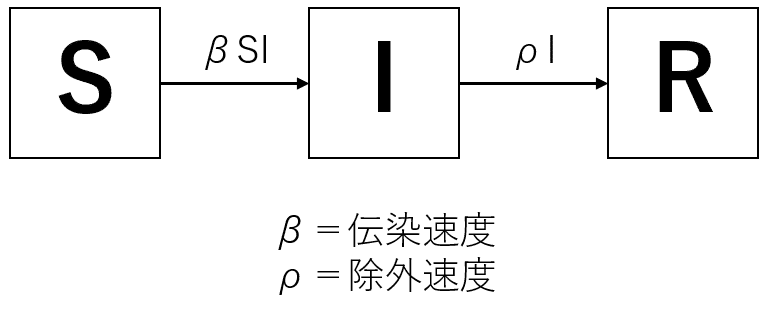
この図の矢印は一日当たりの増加量を意味しているのだった。とすれば、たとえば非感染者のみの増加量に注目すると、次のような式で表すことができる。

（一日当たりの非感染者の増加量）＝-βSZ

βSZにマイナスがついているのは、減るからだ。「いくら増加したか？」を考えるときに減少を表すには負の符号をつければよい。中学校で習ったことだ。
また、同様にして感染者と除外者の一日当たりの増加量はそれぞれ次の通りになる。

（一日当たりの感染者の増加量）＝βSZ-ρI
（一日当たりの除外者の増加量）＝ρI

いちいち「一日当たりの～の増加量」などと書くのは面倒なので、今後は一日当たりの増加量を示すときには、記号にダッシュをつけて書くことにする。すなわち、

S'＝-βSI
I'＝βSI-ρI
R'＝ρI

となる。

SIRモデルの平衡解

さて、それでは式変形をして解析していこう。皆が知りたいのはパンデミックが終息するかどうかだろう。パンデミックが止まるというのは感染者の増加が止まることに等しい。そこで、I'=0として、式変形をしてみる。すると、

I'=0
⇒　βSI-ρI＝0
⇒（βS-ρ）I＝0

第二行から第三行への式変形は「因数分解」だ。（）内の式かIのどちらか片方がゼロになれば第三行の式は成り立ち、感染者の増加は止まる。
I=0のとき感染者の増加が止まるのは当然だろう。感染者がいなくなれば感染者の減少は起こりえず、新規感染者も増えないからだ。一方、βS-ρ=0の場合は感染者の増加と減少が完全につりあって状態を指す。言い換えれば感染者の見かけ上の変化がゼロになっているということで、つまり、非感染者から感染者への変化は起こっていることもある。

高校で化学を習った方にはなじみあるかもしれないが、とにかく実際の、あるいは見かけ上の変化がゼロになっている状態を平衡状態と呼ぶ。そして数学的には、平衡状態になるようなSやIの値を平衡解と呼ぶ。上の議論より、SIRモデルの平衡解には次のふたつが挙げられる。

I=0
または、S=ρ/β

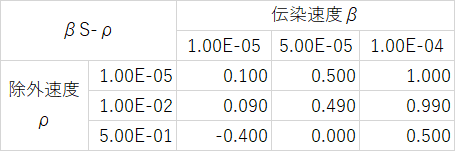
それぞれが具体的に何を意味するのか、SIRモデルの計算で見てみよう。以下にSIRモデルの計算結果を示す。いつものように、S=9999、I=1でシミュレーションを行った。青が非感染者、オレンジが感染者、灰色が除外者を表しているまた、使用したパラメータからρ/βを計算して表にまとめた。

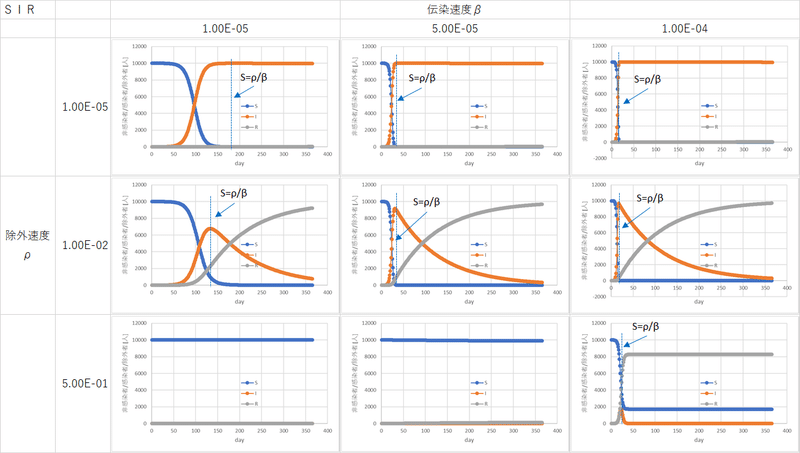
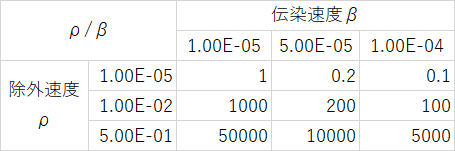
上図の上三列以外では、最終的にI=0になっていることがわかる。また、上三列についてもシミュレーションを続ければいずれはI=0へと収束する。したがって、I=0はシミュレーションを無限に長く続ければどんなパラメータを設定しても出現する。これは、単純なSIRモデルにおいては必ず感染は収束することを意味する。ただ、除外者が恢復者か死亡者かはわからないが。
また、それぞれのシミュレーション結果でS=ρ/βになるタイミングを矢印で示した。図と表から次のふたつがわかる。①S=ρ/βとなるタイミングで感染者数はピークをとる。②ρ/βが感染者数の初期値（上のシミュレーションでは9999人）を上回る場合、感染者は増えない。

①について、「ピーク」というのは増加（I'>0）から減少（I'<0）へ転じる瞬間のことだ。ゆえに、ピークの瞬間にのみI'=0となる。高校数学では「微分係数がゼロになる」という言葉で親しまれている。
次に②について。S=ρ/βというのは、もともとβS-ρ=0から来ていた。この式に上で行ったシミュレーションのパラメータとSの初期値9999を代入すると、以下の通りになる。

I'=（βS-ρ）IにI=1を代入すると得られることから、βS-ρというのは感染者一人あたりによる感染者の増加数なので、それが負あるいはゼロになっている場合には感染者の増加が全く起こらないというわけだ。

以上、I'の式変形からシミュレーションの結果を予測できることを示した。順序としては以下の通りになる。
～解析手法～
　I'=βSI-ρIを因数分解し、I'=（βS-ρ）Iとした
～解析結果～
1. βS-ρが正であれば感染者数は増加する
2. S=ρ/βのタイミングで感染者数はピークをとる
3. シミュレーションを長い時間続けると、必ずI=0となり、感染は収束する

SZRモデルの数的解析

同様に、SZRモデルも式計算で予測してみよう。SZRモデルは次の図で表される。SIR・SZRモデルの紹介記事では除外者からゾンビへの蘇生が含まれていたが、続く記事でζ=0としていたので今後は省略することにする。

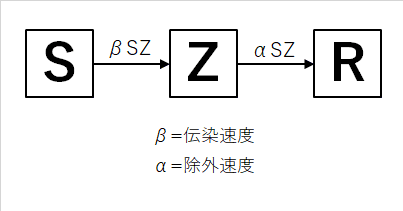
式は次の通りになる。

S'=-βSZ
Z'=βSZ-αSZ
R'=αSZ

今回はZ'に注目して計算を進めよう。

Z'=（β-α）SZ
⇒　Z'=0となるのは、β-α=0, S=0, Z=0のとき

平衡解をひとつずつ見ていこう。

①β-α=0というのは、ゾンビへの感染数とゾンビの破壊数がつり合うことにより、見かけ上の変化がゼロになることを意味する。このとき、確かにゾンビの数は変化しないのだが、その一方でβが正の値をとる限り人間は減り続け、動かない死体の数は増え続ける。したがって、最終的には人類は滅亡する。
また、S、Z、Rいずれの数値も入っていないため、シミュレーションの開始時点にしか関与しない。βはゾンビの増加に関与し、αは減少に関与するので、β-α>0のときゾンビの感染は拡大し、β-α<0のときゾンビの感染は収束を迎える。

②S=0というのは、もちろん人類が滅亡したタイミングを指す。人類が消えうせ、ゾンビが大陸を跋扈する世界の襲来だ。
シミュレーションは必ずS>0から始めるので、この平衡解はシミュレーションが進んだ場合の最終結果のひとつといえる。ただし、SZRモデルの方程式を見る限り、βが正の値をとる限り人間は減り続けるので、最も有力な解ともいえるだろう。

③Z=0というのは、S=0とは逆にゾンビが滅亡したタイミングを指す。
シミュレーションにおいてはS、Zとも正の値をとる。ゆえに、ゾンビが減るためにはβ-α<0、つまりゾンビが増えるよりも速く人間がゾンビを破壊することを意味し、β、αがシミュレーション内で一定の値をとるのであれば先手必勝しかない。初動でゾンビを破壊しつくす以外に人類生存の道はない。

以上、SZRモデルの数的解析によれば、シミュレーション結果は次のように予想される。
～解析手法～
　Z'=βSZ-αSZを因数分解し、Z'=（β-α）SZとした
～解析結果～
1. β-α>0のとき感染者数は増加し、人類滅亡で終息を迎える
2. β-α=0のとき感染者数は増加しないが、人類は減り続け、いずれ滅亡する
3. β-α<0のときゾンビは早い段階でいなくなる。人類は滅亡しない

この解析結果はSZRモデルのシミュレーション結果をよく説明している。

最後に

今回はSIRモデルとSZRモデルの数的解析を行った。中学数学の知識さえあれば解析できる内容としたが、大学数学の知識があればさらに詳細に解析することができる。たとえば、SIR・SZRモデルの方程式は正確には微分方程式とよばれる。微分方程式は行列とベクトルで表され、その際に使われた行列（ヤコビアンとよばれる）の固有値を求めることで、平衡解やシミュレーションのある時点の安定性を知ることができる。余裕があればこちらも解説したい。