
アスカ見参 連結四分割マップの通路、部屋位置を予測する
連結四分割マップについて
アスカ見参には以下のようなマップがあります。

アスカ見参のwikiに「連結四分割」と記載されていたので、以後このように呼びます。
このマップは出現した時点で、部屋の上下または左右に通路が2つずつあるのでこれは連結四分割マップだなという予想は簡単につきます。
そして開幕時点で自分の現在いる部屋が上下or左右は通路の位置ですぐにわかるのですが、上なのか下なのか、右なのか左なのかを判断することはなかなか難しいです。
フロアを巡回する場合はターン数が少なくて済むなるべく短いほうの通路を進みたいし、開幕で敵に囲まれている場合は反対側から敵が来るまで時間のかかる長いほうの通路に入りたいと思ったりするわけですが、どちらが短いほうの通路でどちらが長いほうの通路かがわからないので苦労します。
通路が寄っているほうがマップの中心側になっていたり、通路が壁から離れているほうが長いほうの通路だったりするような気もするんですが、そう思って通路を進むと予想と正反対だったりしてしまうことも多く確信がもてません。
今回は何とかこの連結四分割マップで自分がどの部屋にいるかを判断する方法がないかと考えてみました。
仮説と検証
普段ダンジョンに潜っているときに感じる
・通路が寄っているほうがマップの中心な気がする
・通路が部屋の壁から離れているほうが長い通路な気がする
これらの感覚をもとに
「壁から通路までのマス数が少ないほうが短い通路、壁からのマス数が多いほうが長い通路である確率が高い」
すなわち
「ある部屋において短い通路と長い通路それぞれの壁から通路までのマス数の合計数をで考えた時に、合計数の多いほうが長い通路である確率が高い」
という仮説をたてました。
そしてこれを検証するために次のように各部屋の入口に番号をつけ、それらの入口が壁から何マス目にあるかを調べてみることにしました。

4つの部屋をA,B,C,Dとし、各部屋の入口に画像のように番号をつけ、入口の番号は短いほうの通路を奇数、長いほうの通路を偶数としました。
壁からの距離を数えるときの注意点として
・不定形の部屋の場合は欠けている部分を補完した長方形で考える
・迷路部屋の場合は一番外周の通路を部屋の端と考える
・2マス通路の場合は壁から遠いほうのマスを入口と考える
としています。
上記のマップで数えてみると次のようになります。
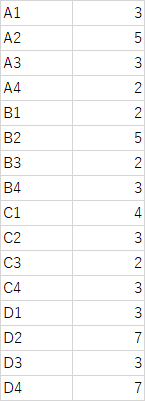
これをいくつかのマップで調べてみて集計してみました。
実際に裏白1Fでマップを採取して20個の連結四分割マップを調べた結果が次の表です。

上の表の見方は
①マップから採取したデータ
各部屋の各入口の壁からのマス数を数えて入力したもの
②全部屋
数えたマス数を短い通路と長い通路に分けてそれぞれの4つの部屋の合計をとったもの
③上下部屋
上下の部屋(部屋Aと部屋C)のみで数えたマス数を短い通路と長い通路に分けてそれぞれの合計をとったもの
④左右部屋
左右の部屋(部屋Bと部屋D)のみで数えたマス数を短い通路と長い通路に分けてそれぞれの合計をとったもの
⑤部屋毎の信頼度
各部屋毎に短い通路の合計数と長い通路の合計数を比較して合計数の少ないほうへ進んだ場合にそれが短い通路であるかどうか
当たっていれば1、ハズレていれば0、合計数が同一の場合は空白とした
となっています。
順番に詳しく説明していきます。
①は裏白の1Fを繰り返して連結四分割が出た時に採取して各部屋の各入口の壁からの距離を調べて入力したデータです。
②は短い通路の合計と長い通路の合計をマップ毎にとったものでほとんどのマップで長い通路のほうが合計値が多くなっています。
全20マップの内、長い通路のほうが多くなったのが16、短い通路のほうが多くなったのが3、同一だったのが1でした。
全20マップの合計で比較した場合も短い通路が463、長い通路が526と長い通路のほうが多くなっています。
これは通路が壁から離れているほうが長い通路である確率が高いと一応言えるのではないでしょうか。
③は上下の部屋のみに対して②と同じように集計したものです。こちらは全20マップの内、長い通路のほうが多くなったのが9、短い通路のほうが多くなったのが10、同一だったのが1でした。なんと、長い通路のほうが少なくなってしまいました。合計数も短い通路が220、長い通路が214と長い通路のほうが少なくなりました。やはり、仮説は間違っているのでしょうか・・・
④は左右の部屋のみに対して②と同じように集計したものです。こちらは全20マップの内、長い通路のほうが多くなったのが16、短い通路のほうが多くなったのが3、同一だったのが1でした。合計数は短い通路が243、長い通路が312とこちらは長い通路が多くなってくれました。
ここまで見てきた感じ、全体としては長い通路のほうのマス数のほうが多くなっていて、一見仮説が正しいように思えるが上下の部屋だけで見ると逆転してしまっていて確信は持てないという感じです。
そこでふと思ったのが、なんか下側の部屋がおかしくない?なんかあたかも上の部屋のようにふるまってなってない?ということです。ここまで上下と左右に分けてみてきましたが、下の部屋がなんか仮説と反対になっていることが多いような気がしました。
なので、今度は部屋毎に仮説に基づいてマス数が少ないほうの通路へ進んだ時に短いほうの通路へ行けるかどうかを調べてみました。それが⑤の部屋毎の信頼度です。
⑤部屋毎の信頼度は各部屋毎に短い通路の合計数と長い通路の合計数を比較して合計数の少ないほうへ進んだ場合にそれが短い通路であるかどうか、
当たっていれば1、ハズレていれば0、合計数が同一の場合は空白としています。1が多ければ仮説通りに進めば当たりやすい、0が多ければハズレやすい、空白の場合は判断のしようがないということです。
例えばAの部屋の場合A1+A3とA2+A4を比較してA1+A3のほうが少なければA1,A3側へ進み、それが短い通路であるかどうかということです。
この結果が次のように意外なものとなりました。
部屋A(上) 当たり16 はずれ3 判断不能1 当たりの確率84%
部屋B(右) 当たり15 はずれ5 判断不能0 当たりの確率75%
部屋C(下) 当たり1 はずれ14 判断不能5 当たりの確率7%
部屋D(左) 当たり14 はずれ3 判断不能3 当たりの確率82%
※当たりの確率は判断不能を除いて算出
なんと、上・右・左の部屋は仮説通りに進むと高確率で当たり、下の部屋だけが仮説通りに進むとかなりの確率で外れるという結果になりました。下の部屋はかなりの嘘つきだったわけです。当たりの確率が7%ということは外れる確率が93%になるので、これは上の部屋の当たりの確率を上回っています。
ということは上側の部屋の当たり確率を考慮しても、開幕で上下の部屋だった場合、仮説と反対方向へ進んだ方が当たりやすいということになります。
上が84%、下の逆が93%なので確率的にはほぼ五分五分に近くはなりますが、反対に進んだ方が少しだけ分が良いです。
まとめ
今回の検証でわかったことをまとめますと以下のようになります。
1.開幕で左右の部屋の時、通路の入口の壁からの距離を右側の通路2つと左側の通路2つに分けてそれぞれ合計して比較し、値の小さい方へ進むと短い通路へ行きやすく、その確率も高い。(確率は70%以上?)
2.開幕で上下の部屋の時、通路の入口の壁からの距離を上側の通路2つと下側の通路2つに分けてそれぞれ合計して比較し、値の大きい方へ進むと短い通路へ行きやすいが、その確率は高くはない。(確率は五分五分に近い?)
3.それぞれ合計した値が同じ場合は今回の方法では判別できない。
以上のことがわかりましたが、検証したマップ数が少ないので100%の確信はないという感じです。今回は検証したマップ数がたったの20なので、もっと多くのマップで検証すれば違った結果になるかもしれません。本当は100以上のマップで検証したかったのですが、連結四分割マップがなかなか出てくれないので20で断念しました。
あと今回の検証中に思ったことがあるのですが
・上下の部屋に比べて左右の部屋のほうが広い?
・上と下を比較すると下側の部屋は小さいことが多い?
というような気がしました。
左右の部屋のほうが大きいのであれば、開幕は左右の部屋から始まる確率が高く、左右の部屋の場合は今回の仮説に基づいて行動すれば有利になります。
また、下の部屋が小さいというのが本当であれば、開幕がかなり小さい部屋であれば下の部屋と割り切って行動することもありかと思います。
これらも今後調べる機会があれば調べてみたいです。
今回の検証は以上です。お読みいただきありがとうございました。
2022/10/23追記 100マップによる追加検証
20マップでの調査をここまで書いてきましたが、後日改めて100マップで追加調査を行ったのでその結果を報告しておきます。
20マップの時と同様に
「ある部屋において短い通路と長い通路それぞれの壁から通路までのマス数の合計数をで考えた時に、合計数の多いほうが長い通路である」
という仮説のもと100個の連結四分割マップに対して調査を行いました。
上下左右の部屋別に集計すると以下の表1のようになりました。

20マップの時と同様に上、右、左の部屋は正しく、下の部屋は正しくないという結果になっています。
判断不能の場合を除いて正解とハズレの確率を求めると以下の表2のようになります。
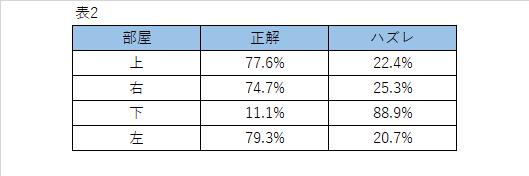
では、実際のダンジョンでどのように行動すればよいのでしょうか。
上下の部屋と左右の部屋に分けて、判断不能の場合も考慮しながら確率を計算してみます。
短いほうの通路へ行きたい場合、合計マスを計算して判断できれば合計数の少ないほうへ、合計数が同じ場合はランダムに移動とするのが現実的かと思います。
したがって短いほうの通路へ行きたい場合は
・合計マス数を計算して少ない方へ移動(確率は上の確率の表のとおり)
・合計マス数が同一の場合は好きな方へ移動(確率1/2)
のように移動することを前提としておきます。
左右の部屋の場合
開幕が右の部屋である確率と左の部屋である確率を同じと仮定すると開幕が左右の部屋のときに前提のとおりに移動して当たる確率は
当たる確率=
1/2(右判断可能率×右当たる確率+右判断不能率×1/2)
+1/2(左判断可能率×左当たる確率+左判断不能率×1/2)
で計算できます。
実際に表1の数字をもとに計算してみると
開幕が左右の部屋の時に自分のいる部屋を判断できる確率は72.8%となりました。
上下の部屋の場合
開幕が上の部屋である確率と左の部屋である確率を同じと仮定します。
そして上下の部屋の場合は下の部屋の外れる確率が上の部屋の当たる確率を上回っているので、前提と逆に動くことにします。
計算式は
当たる確率=
1/2(上判断可能率×上ハズレ確率+上判断不能率×1/2)
+1/2(下判断可能率×下ハズレ確率+下判断不能率×1/2)
で表されます。
こちらも表1の数字をもとに計算してみると
開幕が上下の部屋の時に自分のいる部屋を判断できる確率は54.0%となりました。
ここまでずらずらと検証したことを書いてきましたが、うまくまとめることができずかなり読みにくい内容だったかと思います。最後に今まで検証してきた結論を書きますので、よくわからなかった方は以下だけでも読んで頂ければ幸いです。
結論:連結四分割マップが出た時に短いほうの通路へ行きたい場合は以下のように行動すると正解する確率が高い
① まず通路の位置で自分が上下の部屋にいるのか、左右の部屋にいるのかを判断する
② 部屋の壁から通路までのマス数を上下の部屋ならば上と下に分けて、左右の部屋ならば右と左に分けてそれぞれ合計する
③ 合計した値を比較して値が同じならば、好きな方へ進む
④ 合計した値が異なり上下の部屋の時であれば、合計した値が大きいほうの通路へ進む
⑤ 合計した値が異なり左右の部屋の時であれば、合計した値が小さいほうの通路へ進む
⑥ ①~⑤のように行動すれば、上下の部屋のときは54.0%、左右の部屋のときは72.8%で短い通路に行くことができる
というのが結論です。確率の部分はマップの検証数を増やせば多少は変化してくると思いますが、大きくは変わらないでしょう。
今回の方法では上下の部屋は五分五分、左右の部屋は7割程度で当てることが出来ると考えてよいと思います。
今回は通路までのマス数のみで判断しようと試みましたが、通路の形状などから判断する方法もあるかもしれません。あとは上下の部屋の場合は水路と壁があったりして即座に判断できるケースもあります。
なんで下の部屋だけ当たり確率が極端に低いのか?などまだまだ謎は残りますが、今回の調査はここで終了とさせていただきます。
以上、追加調査の報告でした。お読みいただきありがとうございました。
