
サルでもわかるプライス方程式
プライス方程式(Price equation)は、ある遺伝的な形質の、次世代への伝わり方についての式です(註1)。つまり進化の方程式といってもいいでしょう。この場合の「遺伝的」というのは遺伝子による伝達のみを指すものではなく、例えば文化的な形質が社会的に伝達される場合にも当てはまります。つまり、文化進化についても適用できるということです。さらに、この式を拡張することにより、利他行動が進化する条件についても知ることができます。利他行動の進化については、その要因として血縁淘汰理論と互恵的利他主義の理論が挙げられることがほとんどですが、実はこれらはプライス方程式の拡張によって統一的に理解できます。ここでは、できる限り分かりやすくプライス方程式について説明します。できれば数式は使いたくないのですが、世の中には数式を使った方が分かりやすくなることもあるのですね。というわけで、数式は出てきますが、割り算とか掛け算とか、ごく簡単なものです。式の詳しい展開は省略するので、自分で計算してみてください。
1. プライス方程式とは
世代交代による形質の変化は「淘汰」と「伝達」に分けられるというのが、プライス方程式の「キモ」です。まずは「淘汰」の部分についてみていきましょう。
個体のもつある形質をZとします。例えば身体の大きさであるとか、足の速さであるとかいった個体差のある形質を想定してもらってもかまいません。このZがどれくらい次世代に伝わるかは、個体がその形質をもっている程度と、その形質が次世代にコピーされる数(適応度)をかけた値として表されます。iという個体の形質Zを数値化したものをzi、個体iの適応度をwiとすると、 個体iの形質が次世代に伝わる程度は、両者をかけてzi * wiとなります。
具体例として、4個体からなる集団を考えましょう(図1)。いささか個体数が少ないですが、これは計算を簡単にするためです。形質Zを5という程度でもつ個体(z = 5)が2個体、7という程度でもつ個体(z = 7)が2個体いるとします。そうすると、集団の形質Zの平均値(E(z))は6.0となります。
zが5の2個体は、それぞれ3個体と4個体の子を次世代に残したとします。一方、zが7の2個体はそれぞれ7個体と6個体を残したとします。そうすると、集団の適応度の平均値(E(w))は5になりますね。
各個体の形質Zが次世代に伝わる程度はzi * wiなので、4個体についてこれらを足し合わせ、次世代の個体数で割ったものが、次世代の集団における形質Zの平均値(E’(z))です。次世代の個体数は20個体なので、E’(z)は126を20で割って6.3です。
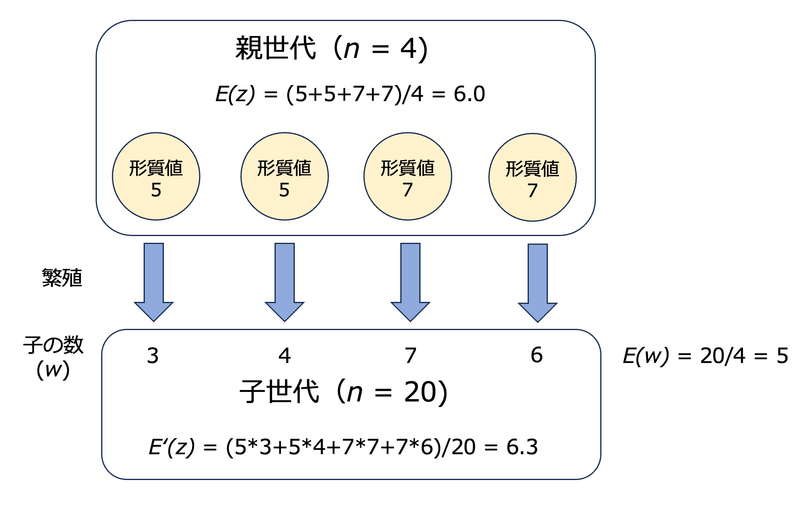
形質Zの変化、つまりE’(z)- E(z)= ΔE(z)は0.3となります。Zは大きくなる方向に進化したわけですが、これは形質が5よりも7の個体の方が多くの子を残していることから、直感的に理解できるのではないでしょうか。以上を数式で書くと以下のようになります(註2)。
$${{\large\Delta E(z)}={\huge\frac{\sum_{i=1}^n z_i * w_i}{\sum_{i=1}^n w_i}-\frac{\sum_{i=1}^n z_i}{n}}}$$ (1)
両辺にE(w)、つまりΣwi /nをかけると、
$${{\large\ E(w)}\ {\large\Delta E(z)}={\huge\frac{\sum_{i=1}^n z_i * w_i}{n}-\frac{\sum_{i=1}^n z_i}{n} \frac{\sum_{i=1}^n w_i}{n}}}$$ (2)
例として考えた集団の数値をこれに当てはめてみましょう。左辺は5*0.3 = 1.5ですね。右辺は126/4から6*5を引いて、こちらも1.5です。
(2)式はzとwの共分散として書くことができます(註3)。つまり、
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\operatorname{\it{Cov}}\left(z_i, w_i\right)}}$$ (3)
これがプライス方程式の「淘汰」の部分です。さて、なぜ共分散なのでしょうか。この場合、形質の偏差と適応度の偏差の積の平均値、ということになります。形質の偏差と適応度の偏差の積が正の方向に大きくなるということは、形質と適応度とのあいだに正の相関があるということです。知っている人もいると思いますが、共分散をそれぞれの変数の標準偏差の積で割ったものが相関係数ですね。つまり、ある形質値が大きければ、それだけ適応度も高くなるという関係があるということです。そのような場合には、次世代において形質値が大きくなる、つまり形質値を大きくする方向に進化が進むということは直感的に理解できるでしょう。逆に、形質の偏差と適応度の偏差の積が負の方向に大きくなると、ある形質値が大きいほど次世代に伝わりにくくなるということなので、形質値が小さくなる方向に進化が進むということです。
次に、「伝達」の部分について考えます。ここまでのモデルでは、世代のあいだでzが変化しないということを前提としていました。つまり、zが5である個体の子は同じ5という値を受け継ぐということです。しかし、場合によってはzが変化することもあります。例えば形質Zに突然変異が起こり、5が6になるかもしれません。その分を考慮したのが「伝達」の項です。これは、各個体の親世代と子世代のzの変化量(zi’- zi)に各個体の適応度wiをかけたものの平均値として表されます。つまり、ある個体のzが5から6になれば1増えたことになるのですが、その個体が残した子の分だけ次世代で増えるということです。親の形質値が子に忠実に伝わるのなら、この項は0とみなしてもかまいません。(3)式にこの「伝達」によって変化する分を加えると、
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\operatorname{\it{Cov}}\left(z_i, w_i\right)+E\left(w_i \Delta z_i\right)}}$$ (4)
となります。これが完全なプライス方程式と呼ばれるものです。
さて、上記のように、共分散の正負が進化の方向を決めるわけですが、それはつまり適応度と形質のあいだに何らかの関係があるということであり、各個体の適応度wiは、以下のように形質ziにある係数をかけたものとして表現することができます。
$${{\large\ w_i}={\large\beta_i z_i+\beta_0}}$$ (5)
形質が変化すると、それにβiをかけた分だけ適応度も変化します。例えば、Zが足の速さだとすると、足が速ければそれだけ捕食者から逃げやすく、生き延びやすいでしょう。結果的に他の個体よりも多くの子を残す、つまり適応度wが上がることになります。足の速さがどれくらい子の数に影響するのか、というのが係数のβiです。β0は形質Zとは関係のない適応度を表しています。適応度が形質の関数であるということは、これを(4)式に代入すると、共分散は形質の分散にβiをかけたものとなるので、
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\beta_i Var(z_i)+E\left(w_i \Delta z_i\right)}}$$ (6)
と書くことができます(註4)。ちなみにVar(zi)とはzの分散のことです。さて、なぜ形質値の分散なのでしょうか。上記のように適応度は形質値の関数なので、数学的には共分散が分散になるということなのですが、前の世代と次世代のあいだで形質値に差がつくためには、そもそも形質がばらついていないといけません。もし全個体のzが同じ値、つまり全くばらつきが無いとしたら、それがコピーされる程度には差がつかないので、次世代のzの平均値は前の世代と同じになるでしょう。逆に、zのばらつきが大きければ、形質値に応じて子の数が変わるので、それだけ次世代のE’(z)は変化しやすくなり、その程度はβiに依存するというわけです。
2. プライス方程式の拡張
さて、(6)式を見て何か気がつかないでしょうか?左辺は平均適応度に形質Zの平均の変化量をかけたものですが、それは右辺の第2項の括弧の中と同じかたちをしています。ということは、ここにもうひとつプライス方程式を入れて、入れ子状にすることができるということです。具体的に説明しましょう。
これまでは、個体からなる集団のなかで、ある形質がどのように変化するのかについて考えてきましたが、入れ子状にするということは、集団を淘汰の単位とみなすということです。つまり、いくつかの集団の集まりをポピュレーションと呼ぶとすると、このポピュレーションのなかで、ある形質がどのように変化するのかについて、集団のレベルと個体のレベルに分けて考えるということになります(図2)。これを複数レベル淘汰(multi-level selection)といいます。
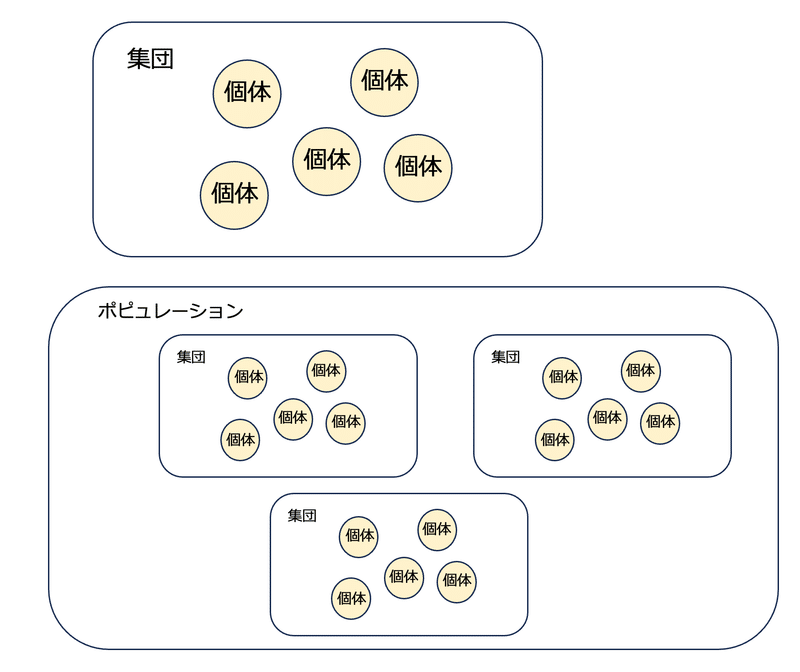
例えばポピュレーションを構成するそれぞれの集団をgとして、その集団内の個体をigとすると、まず集団g内におけるZの変化について、以下のようなプライス方程式を書くことができます。
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\operatorname{\it{Cov}}\left(z_{ig}, w_{ig}\right)+E\left(w_{ig} \Delta z_{ig}\right)}}$$ (7)
次に、この集団をひとつの単位として考えてみましょう。この場合、(7)式のE(w)はそれぞれの集団の適応度wg、ΔE(z)はそれぞれの集団の形質変化量Δzgとみなせます。集団レベルでの淘汰と伝達についてプライス方程式を書くと、次世代集団への伝達はE(wgΔzg)であり、さらに集団間での淘汰を考えて、
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\operatorname{\it{Cov}}\left(z_g, w_g\right)+E({\large\operatorname{\it{Cov}}\left(z_{ig}, w_{ig}\right)+E\left(w_{ig} \Delta z_{ig}\right)})}}$$ (8)
となります。さて、集団gの適応度wgも、やはり集団gがもつ形質zgの度合いに影響されます。その係数をβgとし、(7)式における個体レベルの「伝達」の項を0とすると、(8)式は
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\beta_g Var(z_g)+\beta_i E(Var(z_{ig}))}}$$ (9)
とすることができます。
3. 利他行動が進化する条件
プライス方程式の拡張により明らかになったのが、どのような条件があれば利他行動が進化できるのか、ということです。例えば、集団内のある個体が別の個体に利他行動をして、やり手の適応度はcだけ下がり、受け手の適応度はbだけ上がったとしましょう。つまり、利他行動によって集団のメンバーの適応度はb-cだけ上がることになります。利他行動という形質をどれだけ強くもつかという程度をZとすると、Zの程度にb-cをかけたものが集団の適応度です。つまり、上記の係数βgがb-cです。一方、個体の適応度はZの程度に-cをかけたものとなります。つまり、上記の係数βiが-cです。b-cは正の値であり、-cは負の値です。分散(Var)は二乗値なので必ず正の値ですね。ということは、Zを増やそうとすると、(7)式の左辺のVar(zg)はなるべく大きな、逆にVar(zig)はなるべく小さな値でなければなりません。つまり、集団間の分散は大きく、一方で集団内の個体間の分散は小さい方が、利他行動は進化しやすいということになります。集団間の分散は大きく、集団内の個体間の分散は小さいというのはどういうことかというと、集団内の形質のばらつきが、集団間に比べて小さいということなので、形質の程度、つまり利他性が似たものどうしが集まって集団を形成しているということです。これを「正の同類性」(positive assortment)といいます。
正の同類性が実現されやすいのは、血縁集団です。なぜなら、血縁集団は同じ祖先からきた特定の遺伝子を高い確率で共有しており、また血縁個体どうしは近くにいることが多いので、関わりあう機会も多いからです。血縁どうしのあいだで利他行動がよくみられるのは、そのような理由によるのです。ただ、正の同類性が実現できれば、必ずしも血縁どうしでなくとも利他行動は進化することができます。非血縁間の利他行動の進化を説明するものとして互恵的利他主義の理論がありますが、互恵的利他主義が成り立つためには、フリーライダー、つまりお返しをしない人が排除される必要があります。これはつまり、ちゃんとお返しをする人だけで集団を形成するということですから、やはり正の同類性なのですね。実際、利他性の高い私たちヒトには、正の同類性を保証するための心のしくみが適応によって備わっていると考えられます。例えば、私たちは他者の表情や身ぶりを見ただけで、その人がどれくらい利他的なのかということをある程度正確に判断できるという実験結果があります。どうやら目の周囲の筋肉の動きによって判断しているようなのですが、これは、正の同類性を保つための適応ではないでしょうか(註5)。利他行動の進化については、その説明として血縁淘汰理論と互恵的利他主義の理論、そして間接互恵性が挙げられることがほとんどですが、実はこれらはプライス方程式によって統一的に理解できるものなのです。
註
1) プライス方程式の詳細とジョージ・プライスについては、
オレン・ハーマン (2011). 親切な進化生物学者 ジョージ・プライスと利他行動の対価(垂水雄二 訳). みすず書房
を参照のこと。
プライス方程式と血縁淘汰理論との関係については、
サミュエル・ボウルズ/ハーバート・ギンタス (2017). 協力する種(竹澤正哲他 訳). NTT出版
の訳者による解説を参照のこと。
2) 数学に疎い人のために説明しておくと、Σ(シグマ)とは「全部足し合わせる」という意味である。Δ(デルタ)は「差分」や「変化量」を表す記号。
3) E(XY)-E(X)E(Y)=Cov(X,Y)という関係がある。ちなみにXの分散とは「Xの偏差の二乗の平均」であり、XとYとの共分散とは、「Xの偏差とYの偏差の積の平均」と定義される。偏差とは、平均との差のことである。
4) (6)式の導出の過程を詳しく書いておくと、まず(5) 式を(4)式に代入して、
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\operatorname{\it{Cov}}\left(z_i, \beta_i z_i+\beta_0\right)+E\left(w_i \Delta z_i\right)}}$$
Cov (aX+b,cY+d)=acCov(X,Y)という関係があるので、
$${{\large\ E(w)}\ {\large\Delta E(z)}={\large\operatorname{\beta_i \it{Cov}}\left(z_i, z_i\right)+E\left(w_i \Delta z_i\right)}}$$
ziどうしの共分散とはziの分散のことなので、(6)式を得る。
5) 小田亮 (2011). 利他学. 新潮選書
謝辞
総合研究大学院大学の大槻久さんには原稿を読んでいただき、貴重なコメントをいただきました。ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
