流体力学　２つの質量保存則が等しいことを確認する

おつかれさまです。日々学習したことをまとめています。今回は流体力学の質量保存則について、見出し画像の2式が同じ式つまり互いに必要十分条件であることを復習していきまーす。

質量保存則の復習

そもそも流体力学の質量保存則はこちらの2式です！

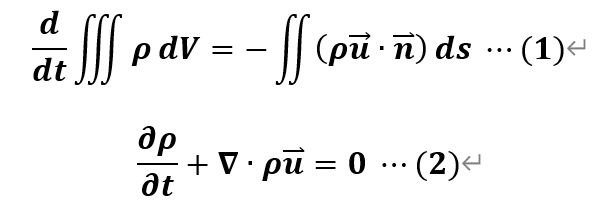
まずこの2式が何を表しているかイメージできないと愛着が湧かないですよね＼(^o^)／

流体力学では（１）式も（２）式も同じく質量保存則を表しています！
じゃーなんで形が違うの？(^o^;
って思いましたが2つの式は導出のアプローチが異なります。

（１）式は積分形つまり有限の大きさの領域に対して積分方程式の釣り合い式を得るアプローチ
（２）式は微分形つまり要素の大きさを無限性にして微分方程式の釣り合い式を得るアプローチ

で導出しているのです！どうしてそれらのアプローチで（１）式と（２）式が導出できるかってところは今回は触れません。とはいえ2式とも質量保存則を表すなら（１）式と（２）式は同じであるはずですよね。

確認してみた

それでは実際に2式が同じであるかを確認していきます！今回は（２）式を変形していって（１）式を導いていきます！逆の手順で（１）式から（２）式に変形できるので（１）式は（２）式の必要十分条件となります。

まず（１）式の右辺に対してガウスの発散定理を用いて式変形をします。

（ガウスの発散定理についてはこちらのnoteも書いています。もし良かったら見てみてください）

つづいて（１,２）式の左辺を変形します。このとき微小体積は空間に固定していて時間変化をしないので体積についての積分と時間についての微分の順番を入れ替えます。

後少しです。（１,３）式を整理すると

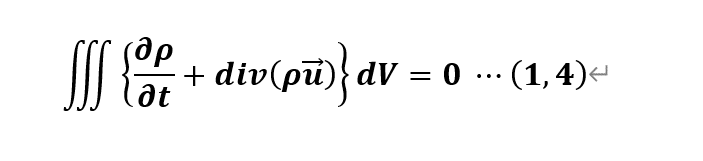
ここで（１,４）式は任意のVで成り立つので

が成り立ちます。ここでdivを∇を用いて表現すると

となり、これは（２）式と一致しました！
逆に（２）式から（１）式も導出できるので（１）式と（２）式は同じ式であることが確認できました！

さいごに

同じ式なのに表し方が2つあるのはややこしいですね。。
基本的に微分形の（２）式で考えられるそうですが、複雑な任意形状を扱う時に積分形の（１）式やガウスの発散定理が登場してくるそうです。

ガウスの発散定理有能すぎですね。

最後まで閲覧していただきありがとうございました！