x + 0.25 - 0.25 = xが成り立たないxとは何か

スタンフォードのコンピュータサイエンスの授業で、ときどきこれは良問と思う問題がテストで出ることがある。僕の印象に残っているのは「xをfloatとするとき、x + 0.25 - 0.25 = xが成り立たないxを求めよ」というものだ。浮動小数点数を理解していないと、両辺が同じにならないケースがあるほうが不自然に思えるだろうから、この問題は浮動小数点数の奇妙さを結構うまく突いていると思う。この問題を元に浮動小数点数についてちょっと説明してみよう。

まずコンピュータ上での数について少し考えてみよう。コンピュータにおける数と、数学の整数や実数は、よく考えてみると全然違う。コンピュータは有限の記憶領域しか持っていないので、無数にある数を表すことが根本的にできない。つまりコンピュータ上の数は「本物の数になるべく似せた別の何か」だ。現実的には、例えば32ビットの数なら2^32パターンしか表せないので、その限られた点を無限に続く数直線上にどう置くか、というのが、コンピュータにおける数の表現の設計の重要なポイントになってくる。

整数型なら単純に0を中心として1ずつ離して点を置いているわけだ。

浮動小数点数ではもうちょっと凝った点の置き方をする。実数のように使える数の体系にしたいので、0に近い極めて小さな数から極めて大きな数までを表せるようにしたいのだが、その範囲に一様に密に点を配置すると全然ビットが足りない。そこで浮動小数点数では、0近傍の小さな数は密に並べて、大きな数は間隔を開けて配置する、ということをしている。具体的な点の密度や間隔はパラメータによって変わってくるが、イメージとしては浮動小数点数は下の数直線のようになっている。

具体例として、2進数で7桁分の記憶領域があるして、それをうまく使って大きな範囲の正の数を表すことを考えてみよう。7桁を単純に整数として全部使うと0000000₂〜1111111₂つまり0〜127を表せるだけだが（"₂"は2進数という意味の表記）、例えばAAA BBBBというように3桁と4桁に区切って次のようにしてみると、文字通りに桁違いに広い範囲の数を表すことができる。

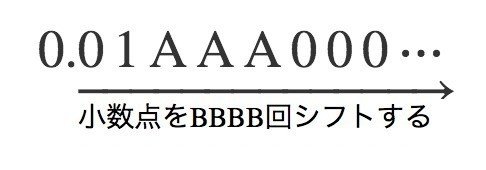
このやり方では、例えば101 0010は0.01 101 000⋯₂の小数点を右に0010₂ = 2桁ずらしたもの、つまり1.101₂を表すということになる。このように小数点記号が動くので浮動小数点数は浮動小数点数と呼ばれている。一般的に書くとAAA BBBBは0.01AAA₂ * 2^BBBB₂を表しているということになる。

いくつか具体的に数を考えてみよう。この方法で表せる一番小さい数は000 0000つまり0.01 000₂ = 1/4 = 0.25で、その次に小さい数は001 0000つまり0.01 001₂ = 1/4 + 1/32 = 0.28125ということになる。同じように、一番大きい数は111 1111つまり1 111 0000000000₂ = 15360で、二番目に大きい数は110 1111つまり1 110 0000000000₂ = 14336だ。小さな数の間隔は1/32だが、大きな数の間隔は1024になっている。

実際にはぴったり0なども表したいので、極めて小さい数の場合は暗黙のうちにくっついてくる1を0にするといった例外ルールなどがあるのだが、基本的な理解としてはこれが浮動小数点数というものだ。

さて、この方法ではAAAの部分にしか好きな数字を入れることができない。1AAA₂と1AAA0₂を比べてみると、1AAA0₂のほうが点の間隔が2倍飛びになっている。2進数では小数点を右に1桁ずらすことで数を2倍大きくすることができるけど、そうすると上のような方法で「次に表すことのできる数」も2倍間隔になってしまう。別の言い方をすると浮動小数点数では、数の大きさに対して点の間隔が常に一定の比に収まっている。

この点の間隔の性質は考えてみればそう悪いものでもない。現実世界の計測値などを考えると、大きな値には大きな誤差が、小さな値には小さな誤差があるのが普通だから、大きな数をそこまで精密に表せなくても実用上困らない、と考えることができる。浮動小数点数はそういう割り切りのもとにデザインされた数の体系なのだ。

さて、一番最初の問題に戻って答えを考えてみよう。答えは2^nという形で答えなければいけなかった。解答を得るためのアイデアは次のとおりだ。0から離れるにつれてときどき点の間隔が2倍になっていくのだから、どこかの点では、数直線の左側の点は0.25しか離れてないけど、次の右側の点は0.5離れている、というものがあるはずだ。それを本物の32ビット浮動小数点数で考えると2^22になる。この値では、0.25を足した数が次に表現可能な数とのちょうど中間で、丸められて2^22に戻ってしまう。しかし0.25引くことは普通にできるので、2^22 + 0.25 - 0.25は2^22 - 0.25になる。これは2^22とは異なる数なので、これが答えの一つということになる。

実際のテストだと、試験対策をしてきているとはいってもこれを5分くらいで考えて解かないといけないので結構大変だ。

JavaScriptだとすべての数が実は64ビット浮動小数点数なので、上のような現象を簡単に観測することができる。ブラウザのデバグコンソールを開いてMath.pow(2, 53)とそれにプラスマイナス1したものを計算してみよう。マイナス1することはできるが、プラス1しても元の数と変わらないことが観測できると思う。JavaScriptである一定の数を足す、というカウンタを作っていると、カウンタがある時から突然増えなくなってしまうのだが、これはつまり上のようなメカニズムによるものなのだ。

浮動小数点数をなんとなく実数と同じだと思って使っていると、奇妙な問題が起こったときにまったく手も足も出ない。ある程度きっちり仕組みを理解しておくことは重要だと思う。

（追記：浮動小数点数で暗黙のうちについてくる1がなぜ必要かというと、0.0 010₂ * 2 = 0.0 001₂ * 4というように、それがないと同じ数を複数の方法で表せるようになってしまう、というのが主な理由。）