グラフ理論

１．グラフ理論とは

数学でグラフと聞くと、2次関数などで扱った座標平面を思い出すかもしれませんが、グラフ理論で扱うグラフはちょっと違います。

点と点を線でつないで、点同士のつながりを見える形であらわしたもの、これをグラフとよびます。これらの点のことを頂点、線のことを枝とよぶことが多いです。

グラフ理論は様々な分野で使われています。

たとえばインターネットのルーティングプロトコルや、言語学で単語同士のネットワーク表現など、モノとモノの関係性に対して有用な分野です。

とはいえ、実際どのように役立っているかは想像しづらいですよね。

そこで、グラフ理論の中でも理解しやすく、日常でも使える（かもしれない）問題について考えてみましょう。

２．オイラーの定理

オイラーの定理は、その名の通りレオンハルト・オイラーさんが考えた定理です。

この定理では、”ある条件を満たすグラフは一筆書きができる”ということを証明しています。

例として、以下の２つの図形を考えてみましょう。

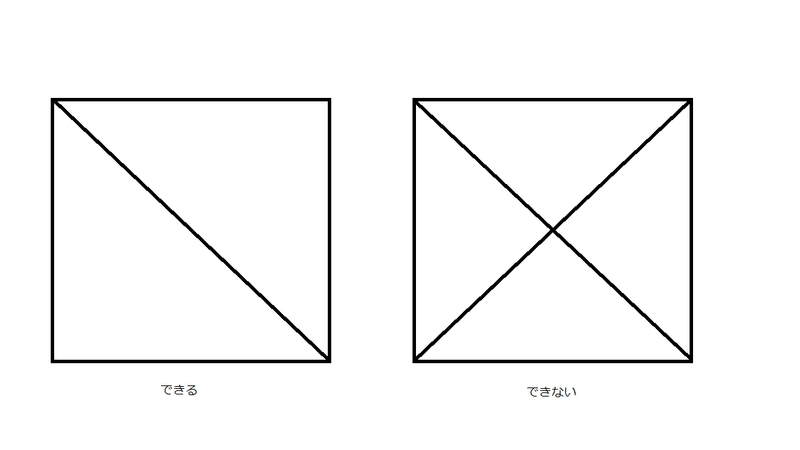
実際にやってみればわかりますが、左の図形は一筆書き可能です。

一方、右の図形は左の図形に1本直線を加えただけですが、一筆書きすることができません。

この2つの図形の違いは一体何でしょうか？

答えは、頂点につながる枝の本数（その頂点の次数とよびます）にあります。

2つの図形の次数を書き出してみましょう。

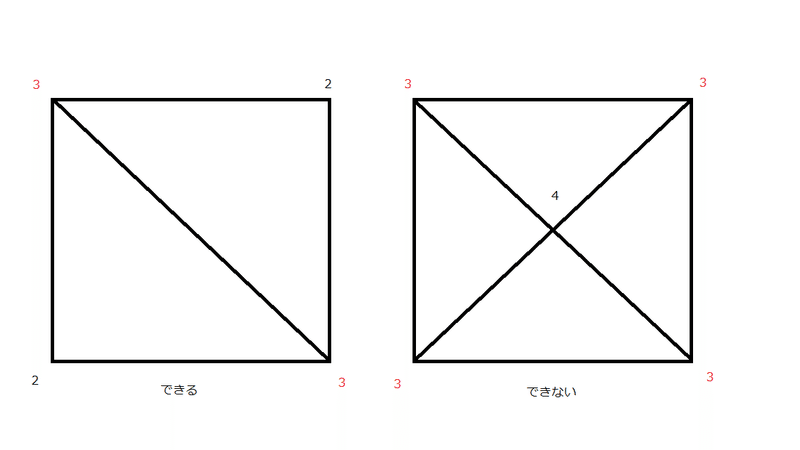
ポイントは、”次数が奇数である頂点が、いくつあるか”です。

左は2つで、右は4つとなっていますが、一筆書きができるのは次数が奇数である頂点が、0個または2個の場合に限ります。

一筆書きの途中で、ある頂点を通過するときを考えてみます。

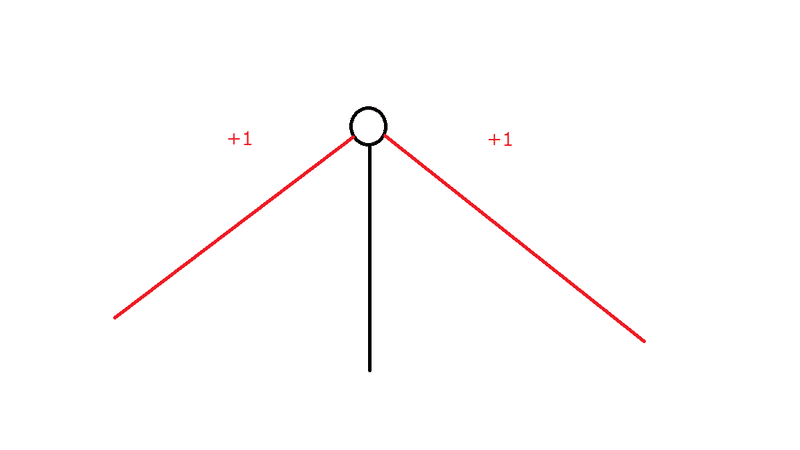
上の図を見ればわかるように、ある頂点に入るときと出るときとで、それぞれ1本ずつ枝を使っています。つまり再びこの頂点を通るためには、さらにあと2本の枝が必要になるのです。

これで、一筆書きの途中経路の頂点は、つながる枝の本数（次数）が偶数であることがわかりました。

頂点に入るだけ、もしくは出るだけならば1本しか枝を使わなくて済むので、始点か終点ならば次数が奇数の頂点を許すことができます。すなわち、次数が奇数の頂点が2個あって、かつそれらが始点と終点ならば一筆書きが可能です。

0個の場合は、どの頂点も出入りできるので、どこからでも一筆書きができるということになります。

３．まとめ

一筆書きができるかどうかは、図形をグラフとしてみたときの次数を見ればわかってしまいます。このように、視覚的に問題が解けてしまうのがグラフ理論の良さだと思います。

ほんのさわりですが、グラフ理論の面白さを感じてもらえましたか？

このほかにもグラフ理論の面白い問題はたくさんあるので、別の機会に紹介したいと思います。