機械学習５：過学習を抑える回帰モデル

こんばんは。自己学習のための機械学習勉強、第５回め。

#過学習を抑える方法

# ①学習（訓練）データの数を増やす
# ②（モデルを簡単なものにする）
# ③正則化を実施する
#「正則化」とは、過学習を防いで汎化性能（未知のデータへの対応能力）を高めるためのテクニックの一つで、モデルに「正則化項」というものを付けることでモデルの形が複雑になりすぎないように調整しようとするもの
→過学習の制御を行うことができる

# リッジ回帰

線形モデルによる回帰の1つである。
# 予測に用いられる式は、正常最小二乗法のものと同じである。Y=w1x1+w2x2...+b
# ここでは、係数の絶対値の大きさを可能な限り小さくしたい。つまり、wの要素をなるべく0に近くにする。“予測をうまく行いつつ、個々の特徴量が出力に与える影響をなるべく小さくしたい（つまり傾きを小さくしたい）。”

#正規化を用いて、過学習を何とかする
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test, y_test)))
”
Training set score: 0.89
Test set score: 0.75
#汎化性能７５％

リッジモデルのパラメーター「α」

# “Ridgeモデルでは、モデルの簡潔さ（0に近い係数の数）と、訓練セットに対する性能がトレードオフの関係になる。

# このどちらに重きを置くかは、ユーザがalphaパラメータを用いて指定することができる。

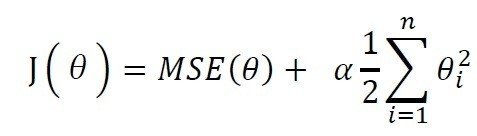
alphaを強くすると？係数も小さくなる（正則化が強くなる）？？

# 先の例では、デフォルトのalpha=1.0を用いた。
# 最良のalphaは、データセットに依存する。alphaを増やすと、係数はより0に近くなり、 訓練セットに対する性能は低下するが、汎化にはそちらのほうがよいかも。

ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge10.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge10.score(X_test, y_test)))
Training set score: 0.79
Test set score: 0.64
#64%

ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge01.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge01.score(X_test, y_test)))
# Training set score: 0.93
# Test set score: 0.77
# #77%

#Lasso

# “リッジ回帰と同様に、Lassoも係数が0になるように制約をかけるのだが、少し違い、こちらはL1正則化と呼ばれる。L1正則化の結果、Lassoにおいては、いくつかの係数が完全に0になる。
#これは 、モデルにおいていくつかの特徴量が完全に無視されるということになる。自動的に特徴量を選択していると考えても良い。いくつかの係数が0になると、モデルを解釈しやすくなり、どの特徴量が重要なのかが明らかになる。”

#“これは、モデルにおいていくつかの特徴量が完全に無視されるということになる。
#自動的に特徴量を選択していると考えても良い 。いくつかの係数が0になると、モデルを解釈しやすくなりどの特徴量が重要なのかが明らかになる。”

from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso.coef_ != 0)))

Training set score: 0.29
Test set score: 0.21
Number of features used: 4

汎化性能が悪い。

Lassoのパラメータ

# “Ridgeと同じようにLassoにも、係数を0に向かわせる強さを制御する正則化パラメータalphaがある。”
#上の例ではデフォルトのalpha =1.0となっていた。
# 適合不足を減らすためには、alphaを減らせばよい。この際、max_iter（最大の繰り返し回数）を デフォルト値から増やしてやる必要がある。
# "max_iter"の値を増やしている。
# こうしておかないとモデルが、"max_iter"を増やすように警告を発する

lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso001.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso001.coef_ != 0)))
#Training set score: 0.90
Test set score: 0.77
Number of features used: 33

# #“alphaを小さくすると、より複雑なモデルに適合するようになり、訓練データに対しても、
# テストデータに対しても良い結果が得られている。性能はRidgeよりも少しだけ良いぐらいだが、104の特徴量のうち、わずか33しか使っていない。これによってモデルは潜在的には理解しやすくなっている。”

実際の活用

# “実際に使う場合には、この2つのうちではリッジ回帰をまず試してみるとよいだろう、しかし、特徴量がたくさんあって、そのうち重要なものはわずかしかないことが予測されるのであれば、Lassoのほうが向いているだろう。同様に、解釈しやすいモデルが欲しいのなら、重要な特徴量のサブセットを選んでくれるLassoのほうが理解しやすいモデルが得られるだろう。scikit-learnには、LassoとRidgeのペナルティを組み合わせたElasticNetクラスがある。実用上は、この組み合わせが最良の結果をもたらすが、それにはL1正則化のパラメータとL2正則化のパラメータの2つを調整するというコストがかかる。