機械学習④ 線形モデル

#線形回帰

#線形回帰 、もしくは通常最小二乗法（ordinary least squares：OLS）は、最も単純で、最も古典的な線形回帰手法である。線形回帰では、訓練データにおいて予測と真の回帰ターゲットyとの平均二乗誤差（mean squared error）が最小になるように、パラメータwとbを求める。平均二乗誤差は、予測と真の値との差を二乗したものの平均値である。

y=ｗ[1]x[1]+w[2]x[2]+....bの形になる

mglearn.plots.plot_linear_regression_wave()

“Out[24]:
w[0]: 0.393906  b: -0.031804”
 

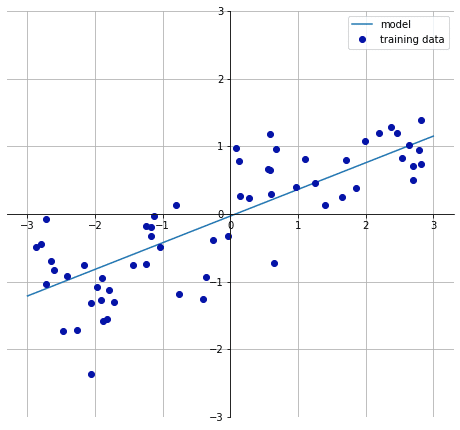
実際にやってみる。

X, y = mglearn.datasets.load_extended_boston()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
​

ｌｒの中身。
# “傾き」を表すパラメータ（w）は、重み、もしくは係数（coefficient）と呼ばれ、coef_属性に格納される。オフセットもしくは切片（intercept、b）はintercept_属性に格納される。”

print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test, y_test)))
# Training set score: 0.95
# Test set score: 0.61

訓練データへの適合が高すぎるため、これは過学習になる。（訓練データへ適合しすぎて、予測ができていない。）

#過学習を抑える方法
# ①学習（訓練）データの数を増やす
# ②（モデルを簡単なものにする）
# ③正則化を実施する
#「正則化」とは、過学習を防いで汎化性能（未知のデータへの対応能力）を高めるためのテクニックの一つで、モデルに「正則化項」というものを付けることでモデルの形が複雑になりすぎないように調整しようとするもの
#過学習の制御を行う

次回へ。