
S&P500って1日や1年にどれくらい上下に変動するものなの?調べてみました。
きっかけはこのXのポストから
新NISAで株を始めた皆様
— chanco@ 損柱 (@chanco09751990) January 19, 2024
この状態でも株を買えますか?🤭
コロナショックの時の米株の様子です🫨 pic.twitter.com/ulKiGvVTS9
数年に1,2回起こる程度の下げなので気になりませんね。私はキャッシュポジションが1%未満のフルインベストのポートフォリオなので何もすることがありませんが。
— らんぶる (@ramblelazy) January 19, 2024
・むしろ買いまくる
— chanco@ 損柱 (@chanco09751990) January 20, 2024
・ただのバーゲンセール
・総悲観は買い
・最高の仕込み場
と、買う言ってる人が非常に多いのですが
実際この状態になったら皆逆のことしちゃうんだよぉぉぉぉ🫨 https://t.co/NDX5vUzeSD
といったことがあり、それじゃあS&P500指数がスタートした1957年3月4日から2023年12月29日(30日、31日は土曜日、日曜日でお休み)のデータを拾ってきて、1日にどれくらい変動するものか調べてみようと思い、作業を進めていくうちに「○○バブル」や「○○ショック」のときはどうだったかも調べてみようという気持ちになり、さらには「GAFAMとか言われているけど、それらってインターネットバブルのときはどうだったの?」と5社についても調べました。
で、Excelで1日や1年での変動幅はどれくらいなのかは比較的早く集計できたのですが、「○○バブル」や「○○ショック」まで手を出したらちょっと時間がかかってしまいましたが、こちらもExcelにチャートを描かせて「ここで○○があった」とか「○○バブルがはじけたり○○ショック前のピークから下落を始めてボトムまで○年○ヶ月かかて、そこからピークの水準まで戻るのに△年△ヶ月かかった」といったことも調べ終わりました。
あとは当時の雰囲気はどうだったのかといったことも手をつけ始めてどんどん手を広げていったことで疲れてきてしまって3月くらいで作業は止まってしまい「あー、早く作業を進めてさっさと終わらせたいなー」と思いつつも他のことをやっていたりしてずーっと頭に引っかかっていたのですが、とりあえず小出しでもいいからできたのだけでもnoteに上げて少しは頭に引っかかっているのを減らそうと思い、今回は「S&P500って1日や1年にどれくらい上下に変動するものなの?」ということで、そもそもこれを始めることになったきっかけの部分を書くことにしました。
1929年の世界恐慌前と後のダウ平均のチャートが手に入ったり、ちょっと前にやたらと「ニフティ・フィフティに似ている」と騒がれていたけどWikipediaを調べたら何故かロシアのWikipediaに日本語で書かれたものがあるのに日本のWikipediaには無かったり、ニフティ・フィフティでワッショイワッショイしていたときにバフェットがとった行動が興味深かったり(自称バフェット信者や自称バフェット研究家なら知っていて当然のことなんだけど、私も調べたことで「あれはニフティ・フィフティのときのことだったのか」と点と点が結びついたりして「おおっ!」となった)といったこともあるけど、それはまた今度ということで。
すでに書いていた部分をそのままつかっていたりするのでいつも以上にヘンなところがあるかもしれませんが、ご容赦を。
最初にS&P500のチャートを眺めてみる
単に日次データをグラフ化すると、このような感じになります。

上昇している長期のデータをグラフ化あるあるですが、昔はほぼ底近くを横ばいで推移し変化が見られませんが、ある時点から上昇を始め、どんどん傾きがキツくなり、最後はほぼ垂直になります。これはこれで正しいのですが、古い期間の変化はほぼ読み取れませんし、直近では急上昇しているので「昔はヨコヨコだけど、最近になって上昇した指数なんだ」と誤解してしまいます。古い期間を数年だけ抜き出してグラフ化するとちゃんと日々上げ下げをしているのが分かります。
1957年からの長期データで変化を見たい場合は、対数グラフで表示します。Excelの場合、縦軸の目盛りの部分をクリックして選択し、右クリックで表示されるメニューから縦軸の設定メニューを表示させ、その中から対数で表示するチェックボックスがありますのでそれをチェックすれば対数グラフになります。その結果が次のグラフです。

縦軸の目盛りが1,10,100,1000,10000と10倍ずつ増えているのが分かると思います。これが対数グラフの特徴です(このように縦軸だけといったように縦軸、横軸のどちらかだけを対数表示にしたのを片対数グラフといい、縦軸と横軸の両方を対数にしたのは両対数グラフと呼ばれたりします)。
対数グラフとして表示するのは、毎日、あるいは毎年○%の複利で上昇している場合、普通にグラフ化すると先ほどのように途中から急上昇したものになるのですが、対数グラフで表示させると仮に毎年10%ずつ増加している場合、ずっと同じ傾きでデータが表示され、元データの数字が大きくなっても10%ずつ増加しているなら昔でも最近でも同じ傾きで表示されます。
資産運用では基本的に複利で考えます。100万円が10%増えた場合と1,000万円が10%増えた場合、金額は違っても資産が増えた割合は同じですから対数グラフでは同じ傾きになります。ですので対数グラフの傾きを見れば資産の大きさに関係なく、その人の運用能力や他人との比較も簡単に分かります。運用している資産に限らず、株価だったりS&P500やダウ平均といった指数の比較でも使えます。
これはExcelだけでなく、日本や米国のYahoo!Financeや、証券会社が提供しているソフトウェアでチャート表示されるものであれば簡単に対数グラフに切り替えることができます。
基本的なことなので「単利と複利」といったことに触れている投資本なら説明されていることですが、もし説明がなかったら著者が忘れているなり片手落ちだったりホニャララな本かもしれませんので、要注意です。
複利といったら「アインシュタインが複利はウンヌンと言った」いうのが有名ですが、Wikipediaでアインシュタインのページを見ていたらこのように記載されていました。
日本のネット上で、アインシュタインが述べたとされるいくつかの言葉が出回っているが、そのほとんどはアインシュタインによるものではない。例としては、「日本が世界の盟主になる」とした予言(アインシュタインの予言や、「『複利』は人類史上最大の発見」とするもの、またそこから派生した「アインシュタインの72の法則」と呼ばれるものなどである。
バフェット関連の書籍を昔から書いているロバート・G・ハグストロームも間違った引用をしていました。
アルバート・アインシュタインの有名な言葉をご存じだろう。「複利で計算する利息は世界の8番目の不思議だ。理解した人はそれを手にし、理解しない人はそれを支払う」。
誰が言い出しっぺなのかは分かりませんが間違った名言の引用や常識を言った人がいて、それが疑われることなく広まって「そっかー、そーなのかー」と信じる人がさらに広めていっていくという、アインシュタインの複利の話は迷信あるあるの1つということも分かりました。こうやって調べていくことからどんどん脱線していくのでした。
1日の変動率は±3~5%以内に収まる
1957年3月4日から2023年12月末までの全営業日数は16,822日(66年9ヶ月)あります。

これをヒストグラム(度数分布表)すると以下のようになります。

1日の変動率が±3%でも99%以上がその範囲内に収まり、±5%となるとほとんどカバーしてしまい、これを外れることの方がまれであることが分かります。
±5%より外に出るのは66年9ヶ月のうち約1ヶ月(36日、0.21%)なのですが、何年に一度のことなのかを計算した結果は以下の通りです。
±5%より外になるのはだいたい1年3ヶ月に1度の割合(36日)。
+5%より上になるのはだいたい3年に1度の割合(15日)。
-5%より下になるのはだいたい2年2ヶ月に1度の割合(21日)。
投資信託の基準価額が1日に5%以上下がると運用会社各社が一斉に今何が起きているのかといった市場分析を含めたコメントを出してきますが、上記のように5%以上下がることがまれであるということから5%がコメントを出す出さないの基準になっているのではないかと思います。
以上がヒストグラムから読み取った1日の変動幅の範囲ですが、これを平均リターンや標準偏差(σ:シグマ)といった統計を使って求めた結果がこちらになります。

細かいことは統計の本なり数学の本なりを読んでいただくとして、ざっくりと説明すると1日1日の変動率の平均を求め、その平均リターンから各データがどれくらい離れているかを計算し、それを標準偏差として求めたとき全体の68.26%は±○%の範囲に収まることになっています(前提条件としてこーなっている場合と仮定しての話なのですが、それこそ統計や数学の小難しい話ですし私もよく分かってないのでそういうものなんだと思ってください)。
上記の表だと1日の平均リターンは0.03%で、それが68.26%の確率で平均リターン0.03%から±1.02%変動するというのが分かります。0.03%±1.02%なので、言い直すと1日に68.26%の確率で-0.98%から1.05%の範囲に収まることが分かります。
求めた標準偏差を2倍にすると、95.44%の確率で平均リターンから±△%の範囲に収まることが分かっています。ですので2標準偏差だと平均リターン0.03%から±2.03%%変動するので、言い直すと1日に95.44%の確率で-2.00%から2.06%の範囲に収まることが分かります。
リスクというと一般的(?)には「損する可能性」として使われることが多いと思いますが、金融の世界でのリスクとは「期待リターンからどれだけブレるか」を指しており、主に2標準偏差が使われることが多いです。一般的に使われているリスクとは意味合いが違ってきます。
「期待リターンより低かったら残念だけど、プラスだったら嬉しいのでいいことではないか」と私もこのことを本で読んだとき思ったのですが、期待リターンが10%だとしたら10%もらえるべきなのですが、それからブレた時点で期待通りの運用ができなかったことになるので(キツい言い方をすれば運用に失敗したとも言える)、期待リターンからのブレをリスクと言い、そのブレかたが大きければリスクが大きく、小さければリスクが小さいとなります。なんかしっくりとこないかもしれませんが、そういうものなんだと思ってください。
ここでヒストグラムから読み取った結果と統計によって計算した結果で違いが出ていますが、データの見方が「俯瞰して見たときは±○%の範囲にこれだけのデータが集まっている」なのか、「各データの平均をとって、その平均から各データがどれだけ上下に散らばっているのを統計的手法によって求めたか」といった、違いからきているのかなーと漠然と思っているのですが、不勉強なので正確なことは分かっていません。どうしても気になる方は統計なり数学の本を紐解いていただくしかないかと思います。
しかしどちらも±3%の範囲に99%以上のデータが集まっていることから、±3%以内なら誤差の範囲。±5%だと「ちょっと大きいけど、まだ誤差の範囲内と言えそうだ」という感じで、これを超えたら「おはぎゃー!」なり「バブルだ!」「暴落だ!」ととにかく騒ぎたい人は騒げばいいかと思います。
ただ1987年のブラックマンデーでは1日でマイナス20%で、その舞台裏では1929年の世界恐慌を再び起こしてはいけないといろんな人が動いているのをNHKのマネー革命の第4回で紹介しており、YouTubeでちょっと前まで見られたのですが、NHKから著作権侵害の申請があったことで削除されてしまい、今は見られなくなりました。
違法アップロード、ダウンロードはダメだけど、YouTubeなどにアップロードされているものを見るのはどうなの?という疑問があるかもしれませんが、文化庁のWebページに以下のものがありました。
ここの(関係資料)の中に、「侵害コンテンツのダウンロード違法化に関するQ&A(基本的な考え方)改正法成立後版」というPDFファイルがあり、その中の「問10 侵害コンテンツを見ただけで違法となってしまうのか。 」に現状の回答が書かれています。
侵害コンテンツのダウンロード違法化に関するQ&A(基本的な考え方)[改正法成立後版](令和2年12月24日文化庁著作権課)
https://www.bunka.go.jp/seisaku/chosakuken/hokaisei/r02_hokaisei/pdf/92746501_04.pdf
問10 侵害コンテンツを見ただけで違法となってしまうのか。
(答)
1.今回の改正によって違法化されるのは、あくまで、侵害コンテンツを意図的・積極的にダウンロードすることであり、侵害コンテンツであっても、単に視聴・閲覧するだけであれば、違法とはなりません(もちろん、政府として、そのような行為を推奨するものではありません)。
2.なお、視聴・閲覧に伴うキャッシュやプログレッシブ・ダウンロードについては、別途、著作権法第47条の4第1項の規定により適法となります。
NHKは公共放送という準国営放送的な存在で、キャラもののグッズを売ったりといった本業以外のことをすれば税金がかかるけど本業に関しては非課税の組織なので、いっそのこと製作した番組は国民の資産ということで全て無料で視聴できるようにしたらいいのにと思うのですが、インターネットの発展に何の貢献もしてないのにインターネット利用者からもお金をセびろうとするなど、とにかく因縁をつけてお金を取ろうとするセコさというか、たかり屋というか、当たり屋というか、人に嫌われることをしてお金を取ろうとする営利企業とは反対の行動を好んでする不思議な存在なので、もしかしたら法律の行間にそう行動するよう書かれていてそれを忠実に実行する脳みそのない人々によって成り立っている組織なのかもしれません。
マネー革命については全3巻の書籍として出ており現在は古本でしか手に入りませんが、1日で50億円損した投機家(実際には180億円とか280億円とも言われており、市場が閉じた時点ではまだ破産してなかったのだが、とある理由により破産になった)の話や、先物市場の会員になって15秒間で120万ドル(約1億5000万円)儲けたトレーダーの話なんかも載っていると思いますので、興味のある方は古本をさがしてみてください。
1年単位だと結構ブレる
次に1年単位(期間は1月1日~12月31日で、初年度は3月4日から12月31日で集計)での変動率(騰落率)ですが、ヒストグラムにすると以下のようになりました。
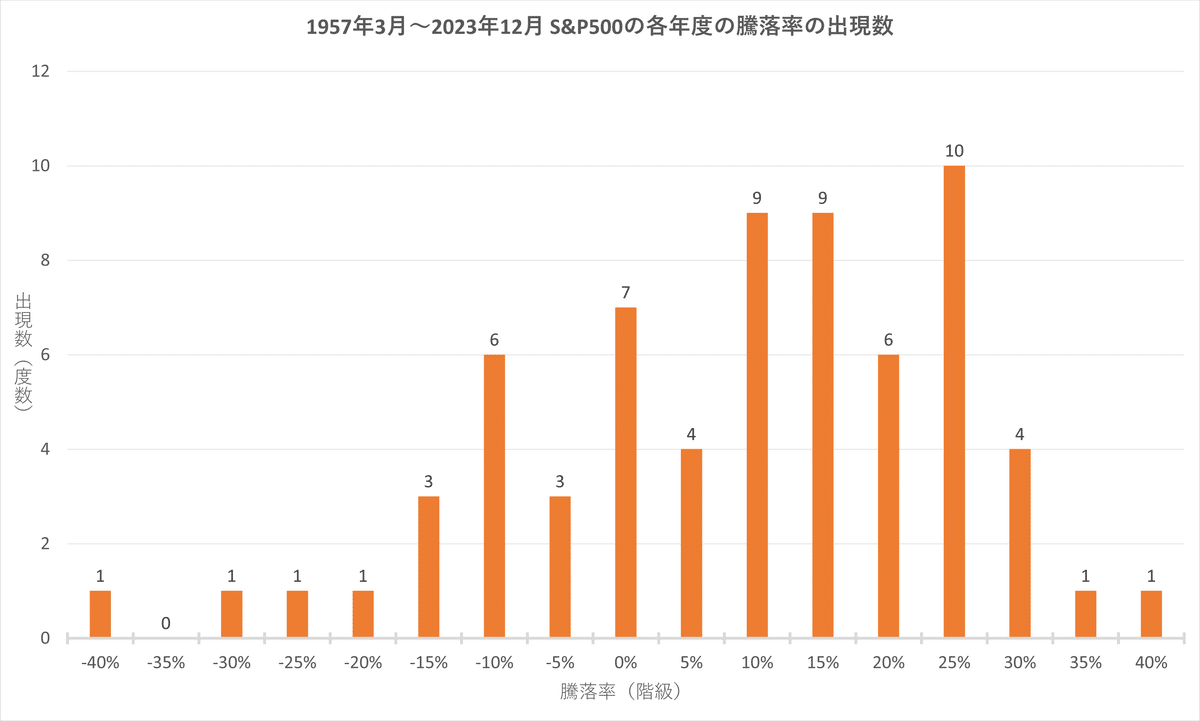
このヒストグラムを見る限り、1日あたりの変動率とは違ってどこかに集中しているわけではないことが分かります。というわけで統計的手法によって平均リターンと標準偏差を求めた結果がこちらになります。

本にもよりますが、株式の平均リターンは7~10%のどこかとして書かれていることが多いため、この8.59%というのは間違ったものではないと言えそうです。
あとは標準偏差(リスク)なのですが、2標準偏差(約95%の確率)だと-24.11%~41.28%のどこかになることが分かります。
最大リターンは38.06%のため2標準偏差の中に収まっていますが最小リターンは-38.49%と2標準偏差から外に出ており、またヒストグラムを見ると-24.11%より小さい年は約66年のうち3回あったことから22年に1回くらいは「暴落」と言ってもいい年があるのが分かります。
とりあえず分かったこと
簡単に列挙すると
1日に3~5%の変動は当たり前のことなので、この範囲内の変動で騒ぐのはかなりのレバレッジをかけているか賑やかし屋のどちらかと言えそう
1年単位で見ると22年に1回の割合で予想外の下落がある
と言えそうです。
ただし、下落や上昇は数年にわたって続くこともありますが、上昇は何年、下落は何年続くといたルールがあるわけではないので、今年はこうだったから来年もこうなると言い切れないところが難しかったり面白かったりする部分かもしれません。
1929年の世界恐慌のときは1932年まで約3年かけてダウ平均は下落しており、恐慌前のピークに戻るまで25年かかっています。先日Xに上げたチャートを以下に貼っておきます。

これについて、ベンジャミン・グレアムはその著書「証券分析(1934年版第1版)」の中でこう述べており、ちょっと違った見方をしていて面白いです。
われわれは1927~33年の出来事が将来の投資のあり方を判断する適切な基準になるという一般的な考えを受け入れることはできない。しかし、この時期の相場の変動ぶりはあまりにも異常であり、将来にはこのような事態は二度と起きないだろうという考えにはそれなりにうなずける。つまり、この時期の出来事はかつての南海泡沫事件に酷似した経済現象であり、将来の一般的な相場の循環を示唆するものではなく、単なる異常なギャンブル的熱狂相場であったと言えなくもない。「投機」の経験に照らしても、最近の出来事はこれまでの事態とはまったく異なっており、「投資」に対する影響という点でも二度と起きないようなユニークな特徴を持つ事態であると言ってもよい。
最近、証券分析の第6版(1940年版)が発売され購入しているのですがまだ未読なので、この見方が変わったかどうか調べてみたいところです。
あと誰もが株なんか買いたいとは思わない1932年頃に買っていれば長いこと上昇相場に乗れることから、総悲観で誰もが株を買おうと思わないどころか口にすることも嫌がるくらいのときに買うのが本当の逆張りで、バリュー投資家かどうか試される場面でもあると言えそうです。
ここにきて一番最初のXのポストに戻りますが、このヒートマップがいつのものか分かりませんが、コロナショックのときのヒストリカル・データを調べたところ以下のようになっていました。
1日の最大の下落率
2020年3月16日(月)
S&P500 -11.98%
DOW -12.93%
この日だった場合-5%を超えているので騒いでもいいですが、むしろめったに起こらないことを見ることができて喜ぶべきかもしれません。
この記事が気に入ったらサポートをしてみませんか?
