
【量子コンピュータ基礎】量子ビットとは
量子コンピュータの基礎を理解するうえで、大切な内容を解説していこうと思います。今回は、量子ビットについて解説します。
(こちらの記事は、以前Qiitaに投稿した内容の書き直しです。)
量子ビットとは
量子ビットとは、普通のコンピュータで使用されている「ビット」の量子版です。この量子版のビットを使って情報を表現し、情報処理を行うのが量子コンピュータです。
古典ビット
量子ビットの説明に入る前に、私たちが普段使っているコンピュータの場合を考えてみましょう。普段の生活で使うコンピュータやスーパーコンピュータは、「古典コンピュータ」と呼ばれています。ここで古典というのは、「量子を用いていない」ということを意味しています。

古典ビットとは、情報の最小単位のことです。そして、このビットは0または1の2つの値で表現されます。コンピュータでは、文字や数字といった様々な情報を沢山のビットを使って表現することで情報処理を行っています。例えば、「りょうし」という言葉をコンピュータで表現するとこんな感じになります。(あくまでもイメージです。)

量子コンピュータでは、ビットの量子版である量子ビットを情報の最小単位として扱います。結論から申し上げると、量子ビットはベクトルです。さらに詳しく説明すると、二次元複素ベクトル空間の単位ベクトルで表現されます。
ブラケット表記
古典ビットでは、0と1という値で表現されていました。量子ビットも同じように、0と1を使って表現されます。しかし、少しだけ表記が異なります。それが、ブラケット表記です。
ケット
量子ビットは$${\ket{0}}$$と$${\ket{1}}$$という記号で表現されます。$${\ket{}}$$という記号は、ケットと呼ばれベクトルを表しています。具体的には、
$$
\ket{0} =
\begin{pmatrix}
1 \\ 0
\end{pmatrix},\,
\ket{1} =
\begin{pmatrix}
0 \\
1
\end{pmatrix}
$$
という列ベクトルで表現されます。これらのベクトルは、単位ベクトルであり、互いに直行するベクトルになっています。
重ね合わせ状態
古典ビットと量子ビットの大きな違いは、$${\ket{0}}$$と$${\ket{1}}$$以外の値もとることができる点です。そしてこのような量子状態を、重ね合わせ状態と呼びます。この重ね合わせ状態を先ほどのブラケットの表記を使って、表現すると次のようになります。
$$
\ket{0} = \alpha\ket{0} + \beta\ket{1} =
\alpha
\begin{pmatrix}
1 \\
0
\end{pmatrix}
+\beta\begin{pmatrix}
0 \\
1
\end{pmatrix} =
\begin{pmatrix}
\alpha \\
\beta
\end{pmatrix}
$$
この$${\alpha}$$と$${\beta}$$は確率振幅と呼ばれるもので、複素数です。この重ね合わせ状態は、$${\ket{0}}$$と$${\ket{1}}$$の値を同時に表現しています。つまり、量子ビットは$${\ket{0}}$$と$${\ket{1}}$$の値を同時にとることができます。これは、古典ビットでは起こりえないことであり、量子ビット特有の性質なのです。
確率振幅の意味
さて、この確率振幅と呼ばれる$${\alpha}$$と$${\beta}$$は何を意味しているのでしょうか。結論から答えると、これらの複素数(確率振幅)は、$${\ket{0}}$$か$${\ket{1}}$$を得られる確率を与えてくれます。これはどういう意味でしょうか。
古典ビットの場合、そのビットを読みだした際には、必ず0または1の結果を返してくれます。量子ビットに関しても、その量子状態を観測した時に、$${\ket{0}}$$または$${\ket{1}}$$の状態を出力します。しかし、その出力結果はランダムなものであり、数回程度の測定ではランダムな$${\ket{0}}$$と$${\ket{1}}$$の無意味な結果が得られるだけです。
そこで、何度もこの測定を行います。すると、統計的に$${\ket{0}}$$と$${\ket{1}}$$のうち、どちらの方が出力されやすいか、つまり、どれくらいの確率でその$${\ket{0}}$$または$${\ket{1}}$$が出力されるかが分かります。実はこの確率というのが、確率振幅の絶対値の二乗で求めることができるのです。
つまり、量子状態が$${\ket{0} = \alpha\ket{0} + \beta\ket{1}}$$の場合、
$${\ket{0}}$$が得られる確率: $${|\alpha|^2}$$
$${\ket{1}}$$が得られる確率: $${|\beta|^2}$$
となります。また、確率なので$${|\alpha|^2+|\beta|^2=1}$$となります。
具体例1
$${\alpha_1=1, \beta_1=0}$$
$$
\ket{\psi_1}=\alpha_1\ket{0}+\beta_1\ket{1}=\ket{0}
$$
量子ビットが、$${\ket{0}}$$という状態です。この場合当然ながら、確率$${|\alpha_1|^2=1}$$で$${\ket{0}}$$が検出されます。
具体例2
$${\alpha_2=1/\sqrt{2}, \beta_2=1/\sqrt{2}}$$
$$
\ket{\psi_1}=\alpha_2\ket{0}+\beta_2\ket{1}=\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}
$$
この場合は、重みの等しい重ね合わせ状態となります。つまり、$${\ket{0}}$$と$${\ket{1}}$$を得られる確率がそれぞれ1/2となります。
ブラ
さて、ブラケット記号のケットは、列ベクトルを表すことを学びました。それでは、ブラは何を意味するのでしょうか。ブラは$${\bra{}}$$という記号で表現され、ベクトルの転置と複素共役を同時にとったものです。
それでは、具体的に考えてみましょう。今ここで、とある量子ビット
$$
\ket{\psi} = \alpha\ket{0} + \beta\ket{1} =
\begin{pmatrix} \alpha \\
\beta
\end{pmatrix}
$$
を考えます。まずこのベクトルの転置は次の行ベクトルとなります。
$$
(\alpha, \beta)
$$
そして、転置して得られた行ベクトルの複素共役は
$$
(\alpha^*, \beta^*)
$$
となります。この操作は、以下のような記号(ダガー)をつかって表現されます。
$$
\ket{\psi}^{\dagger} = (\alpha^*, \beta^*)
$$
これをエルミート共役と呼び、また以下のようにブラを使って記述されます。
$$
\bra{\psi} = \ket{\psi}^{\dagger}
$$
内積
このブラケット記号を使うと2つの複素ベクトルの内積を計算することができます。ここで、ベクトル$${\ket{\psi} = \alpha\ket{0} + \beta\ket{1}}$$を使って具体的に考えてみましょう。この時、内積はブラケット表記を使って
$$
\braket{\psi|\psi} =(\alpha^*, \beta^*)
\begin{pmatrix}
\alpha\\
\beta
\end{pmatrix}
=|\alpha|^2+|\beta|^2=1
$$
また、異なるベクトル$${\ket{\Psi}=i\ket{0}+j\ket{1}}$$との内積は、
$$
\braket{\Psi|\psi} =(i^*, j^*)
\begin{pmatrix}
\alpha\\
\beta
\end{pmatrix}
=i^*\alpha+j^*\beta
$$
となります。
単一量子ビットの測定
量子ビットの量子状態は、測定をすることでその量子状態が変わります。もし量子ビットを測定した結果、$${\ket{0}}$$が得られた場合、量子状態は$${\ket{0}}$$に、$${\ket{1}}$$が得られた場合、量子状態は$${\ket{1}}$$に変化します。測定によって、量子状態が$${\ket{0}}$$や$${\ket{1}}$$といった基底に射影されるので、この操作を射影測定と呼びます。
この射影測定を演算子を使って記述することができます。例えば、$${\ket{0}}$$および$${\ket{1}}$$への射影測定の演算子は、それぞれ
$$
\hat{P_0}=\ket{0}\bra{0}, \hat{P_1}=\ket{1}\bra{1}
$$
となります。先ほど、量子ビットの状態が、$${\ket{0} = \alpha\ket{0} + \beta\ket{1}}$$で与えられた時、
$${\ket{0}}$$が得られる確率: $${|\alpha|^2}$$
$${\ket{1}}$$が得られる確率: $${|\beta|^2}$$
となることを学びました。こちらも、射影測定の演算子を使って確認することができます。例えば、$${\ket{0}}$$に対しての射影測定は、
$$
\bra{\psi}\hat{P_0}\ket{\psi}=\braket{\psi|0}\braket{0|\psi}=|\alpha|^2
$$
となり、$${\ket{1}}$$に対しての射影測定は、
$$
\bra{\psi}\hat{P_1}\ket{\psi}=\braket{\psi|1}\braket{1|\psi}=|\beta|^2
$$
となります。
ブロッホ球
ブロッホ球とは、量子ビットの状態を分かりやすく視覚的に表現するためのツールです。古典ビットは、0または1に決まっている一方で、量子ビットに関しては、具体的にその量子状態をイメージすることが非常に難しいです。しかしブロッホ球を用いることで、単一の量子ビットの状態を直観的に理解できるように表現できます。今、$${\ket{0}}$$と$${\ket{1}}$$の重ね合わせ状態の量子ビットを考えます。
$$
\ket{\psi}=\alpha\ket{0}+\beta\ket{1}
$$
さて、確率振幅$${\alpha}$$と$${\beta}$$には$${|\alpha|^2+|\beta|^2=1}$$という規格化条件がありました。これを利用して、次のように$${\alpha}$$と$${\beta}$$を置き換えてみます。
$$
\alpha=\cos{\frac{\theta}{2}}e^{ia}, \beta=\sin{\frac{\theta}{2}}e^{ib}
$$
すると、量子ビットの状態は、
$$
\ket{\psi}=\cos{\frac{\theta}{2}}e^{ia}\ket{0}+\sin{\frac{\theta}{2}}e^{ib}\ket{1}=e^{ia}(\cos{\frac{\theta}{2}}\ket{0}+\sin{\frac{\theta}{2}}e^{i(b-a)}\ket{1})
$$
となります。ここで、$${e^{ia}}$$という位相は、グローバル位相と呼ばれるものであり、実は物理量として観測することができません。そこで、このグローバル位相を無視し、さらに$${\ket{0}}$$と$${\ket{1}}$$の相対位相$${e^{i(b-a)}}$$を$${e^{i\phi}}$$と定義して、量子ビットを書き直すと
$$
\ket{\psi}=\cos{\frac{\theta}{2}}\ket{0}+\sin{\frac{\theta}{2}}e^{i\phi}\ket{1}
$$
となります。このベクトルは、下図のような3次元の球面上の点を表しています。

また、この球の半径は規格化条件から1となります。この球を、ブロッホ球と呼び、量子ビットの量子状態を視覚的に表現できます。それでは、具体例考えてみましょう。
具体例1: ブロッホ球の北極
$${\theta=0}$$の時、
$$
\ket{\psi}=\cos{\theta}\ket{0}+\sin{\theta}e^{i\phi}\ket{1}=\ket{0}
$$
となり、量子ビットは北極を指します。

一方で$${\theta=\pi}$$の時は、南極を指すベクトルになり、$${\ket{1}}$$に一致します。
具体例2: ブロッホ球の赤道
次に、重ね合わせ状態にある量子ビットをブロッホ球上で表示することについて考えてみましょう。重ね合わせ状態の例として、重みの等しい重ね合わせ状態、つまり、$${\theta=\pi/2}$$の時を考えてみます。すると、量子ビットの状態は、
$$
\ket{\psi}=\frac{1}{\sqrt{2}}(\ket{0}+e^{i\phi}\ket{1})
$$
となり、下図のようにブロッホ球の赤道上の点を表現しています。
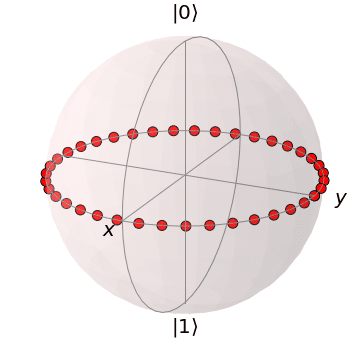
ここから、$${\ket{0}}$$と$${\ket{1}}$$の相対位相($${\phi}$$)を指定することで、特定の重ね合わせ状態を表現できます。例えば、$${\phi}$$= (a) 0, (b) π/2, (c) π, (d) 3π/2のブロッホ球は以下のようになります。

