
【量子コンピュータ基礎3】量子ゲートと量子回路
量子コンピュータは、量子ビットを上手に制御することで所望の情報処理を行います。量子ビットを制御するために、必要となるのが量子ゲートです。さらに、量子ゲートをどのような順序で量子ビットに作用させるのかを教えてくれるのが量子回路です。今回は、そんな量子ゲートと量子回路について学びたいと思います。
古典論理回路
量子回路について考える前に、古典コンピュータの場合について考えてみましょう。古典コンピュータは、論理回路と呼ばれるデジタル回路によって構成されています。下の図は、論理回路の例です(回路は適当です)。

量子回路
量子コンピュータの場合にも、古典コンピュータと同じように、複数の量子版の論理ゲートからなる回路を使って情報処理を行います。こちらが一例です。

入力として3個の量子ビットが用意されています。それぞれの量子ビットが、左から右へ配線をたどっていき、複数の量子ゲートからなる演算が量子ビットに作用します。
初期状態
まず、計算の始まりの部分です。量子計算は、多くの場合$${\ket{0}}$$を初期状態とします。この図の場合、初期状態は3個の量子ビットのテンソル積、つまり
$$
\ket{\psi}=\ket{0}\otimes\ket{0}\otimes\ket{0}=\ket{000}
$$
に準備されています。
量子ゲート
量子ビットにどのような操作を加えるのかを示してくれるのが、量子ゲートです。量子ゲートには、様々な種類が存在します。詳しい解説は、後ほど行いたいと思います。
観測
回路の最後の部分は、量子ビットの射影測定です。メーターのような記号で表現します。
量子ゲート
上述したように、量子計算では量子ビットに対して、量子ゲートを与えることで情報処理を行います。量子ゲートには、
1個の量子ビットの量子状態を制御する単一量子ビットゲート
2個以上の量子ビットが関係する複数量子ビットゲート
があります。
単一量子ビットゲート
単一量子ビットゲートは、量子回路の記号で表すと以下のようになります。

$${U}$$の部分が、量子ビットに作用するゲートを示します。この図の場合、$${\ket{\psi}}$$という量子状態の量子ビットが入力され、出力状態は
$$
\ket{\psi^\prime}=U\ket{\psi}
$$
となります。さて、この単一量子ビットゲートは、数学的にどのように記述できるでしょうか。結論から答えると、単一量子ビットゲートは、2×2の複素行列で記述されます。単一量子ビットゲートは、単一量子ビットの量子状態を操作するものでした。また、単一量子ビットは、
$$
\ket{0}=\begin{pmatrix}
1\\
0
\end{pmatrix},\,
\ket{1}=\begin{pmatrix}
0\\
1
\end{pmatrix}
$$
を基底として、
$$
\ket{\psi}=\alpha\ket{0}+\beta\ket{1}=\alpha\begin{pmatrix}
1\\
0
\end{pmatrix}
+\beta
\begin{pmatrix}
0\\
1
\end{pmatrix}
=\begin{pmatrix}
\alpha\\
\beta
\end{pmatrix}
$$
のように、二次元複素ベクトルとして記述できることから、単一量子ビットゲートは、2×2の複素行列で記述されます。
ここで、少し簡単な単一量子ビットゲートを使った単一量子ビットの制御をみていきましょう。量子ゲートを用いた量子ビットの制御のイメージを掴んでいただくために、ブロッホ球を用いたアニメーションで簡単に解説します。

この量子回路は、入力として一つだけの量子ビットが準備されています。初期状態が$${\ket{0}}$$として入力された後、$${H}$$や$${Z}$$といった記号がついた単一量子ビットゲートが与えられています。
まず一つ目の量子ゲート$${H}$$は、量子ビットを重ね合わせ状態にするゲート操作です。

そして、二つ目の量子ゲート$${Z}$$は、$${\ket{0}}$$と$${\ket{1}}$$の相対位相を$${\pi}$$度回す操作になります。

このように、単一量子ビットの量子状態をゲート操作を与えることで、制御していきます。それでは、具体的な単一量子ゲートを見ていきましょう。
Xゲート
一番分かりやすい単一量子ビットゲートの例として、$${X}$$ゲートを考えます。$${X}$$ゲートは、古典コンピュータにおける論理回路のNOTゲートに対応するゲート操作になります。
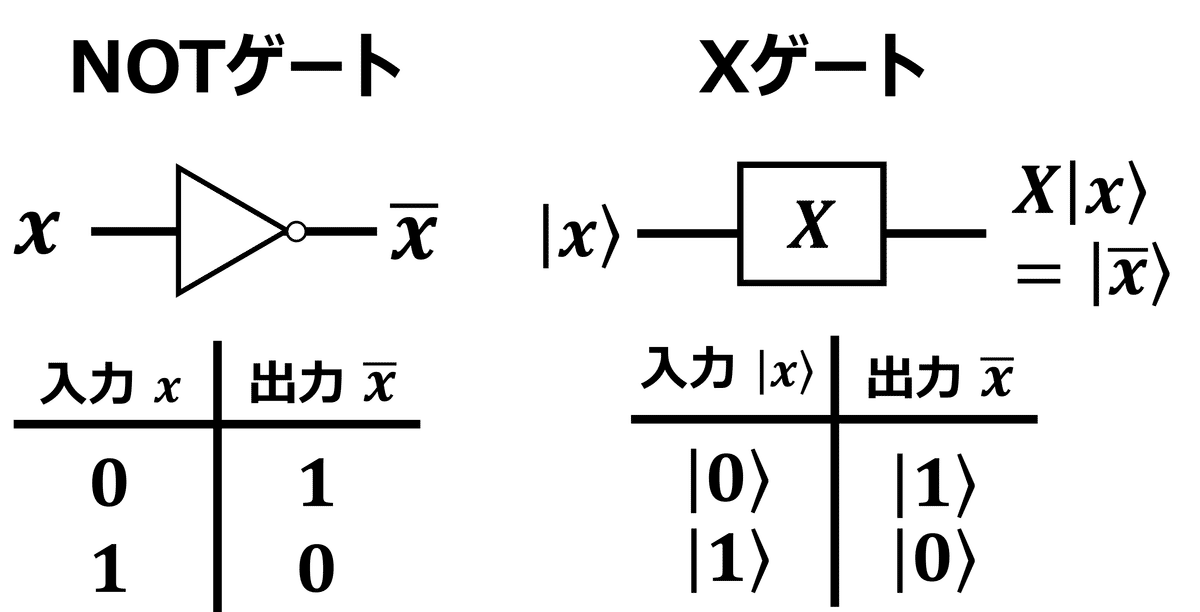
$${X}$$ゲートは以下のように量子ビットを反転させます。
$${X\ket{0}=\ket{1}}$$
$${X\ket{1}=\ket{0}}$$
$${X(\alpha\ket{0}+\beta\ket{1})=\alpha\ket{1}+\beta\ket{0}}$$
では、行列でこの$${X}$$ゲートを表現するとどうなるでしょうか。$${X}$$ゲートの働きは、次のように記述できます。
$$
\begin{cases}
X\ket{0}=X\begin{pmatrix}
1\\
0
\end{pmatrix}
= \begin{pmatrix}
0\\
1
\end{pmatrix}=\ket{1}
\\
X\ket{1}=X
\begin{pmatrix}
0\\
1
\end{pmatrix}=
\begin{pmatrix}
1\\
0
\end{pmatrix}
=\ket{0}
\end{cases}
$$
ここで、$${X}$$ゲートを
$$
X=
\begin{pmatrix}
a & b
\\
c & d
\end{pmatrix}
$$
としたとき、それぞれの成分は、$${a=0, b=1, c=1, d=0}$$となります。つまり、$${X}$$ゲートは、以下のような2×2の行列で表現されます。
$$
X=
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
$$
また、ブラケット表記を使っても$${X}$$ゲートを記述することが可能です。
$$
X = \ket{0}\bra{1}+\ket{1}\bra{0}
$$
例えば、$${\ket{0}}$$に$${X}$$ゲートを与えると、
$$
X\ket{0}=(\ket{0}\bra{1}+\ket{1}\bra{0})\ket{0}=\ket{1}
$$
というように記述できます。また、初期状態$${\ket{0}}$$に対する$${X}$$ゲートの操作をBloch球上で表現するとこのようになります。
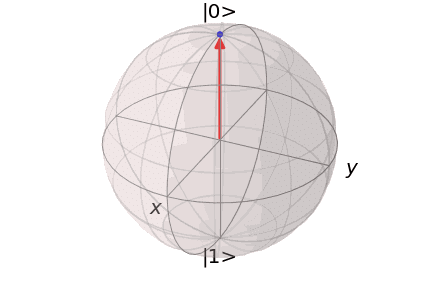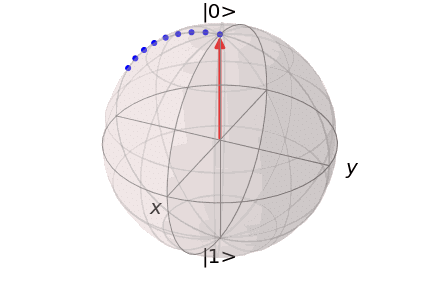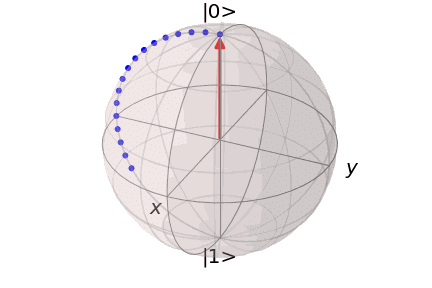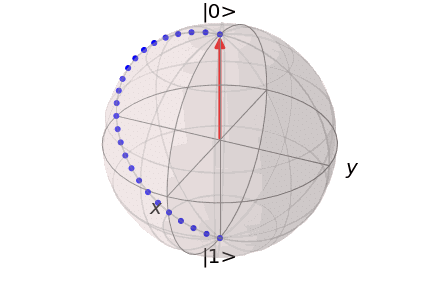
つまり、Bloch球の$${x}$$軸に関する量子ビットの180度回転と理解することができます。
Zゲート
$${Z}$$ゲートは、量子ビットの位相を反転させる単一量子ビットゲートです。
$${Z\ket{0}=\ket{0}}$$
$${Z\ket{1}=-\ket{1}}$$
$${Z(\alpha\ket{0}+\beta\ket{1})=\alpha\ket{0}-\beta\ket{1}}$$
つまり、$${Z}$$ゲートは、$${\ket{0}}$$と$${\ket{1}}$$の相対的な位相を反転させます。$${Z}$$ゲートを行列で表現すると、
$$
Z=\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
$$
となり、ブラケット表記では
$$
Z=\ket{0}\bra{0}-\ket{1}\bra{1}
$$
と記述できます。また、$${Z}$$ゲートの操作をBloch球上で表現することを考えます。分かりやすいように、等しい重みの重ね合わせ状態にある量子ビット$${\ket{\psi}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})}$$に、この$${Z}$$ゲートを作用させた時を考えてみます。

つまり、Bloch球の$${z}$$軸に関する量子ビットの回転と理解することができます。
Yゲート
$${Y}$$ゲートは、
$$
Y = iXZ
$$
と記述できます。つまり、量子ビットを反転させる$${X}$$ゲートと量子ビット間の位相を反転させる$${Z}$$ゲートを組み合わせたゲート操作であることが分かります。
$${Y\ket{0}=i\ket{1}}$$
$${Y\ket{1}=-i\ket{0}}$$
$${Y(\alpha\ket{0}+\beta\ket{1})=i(\alpha\ket{1}-\beta\ket{0})}$$
$${Y}$$ゲートを行列で表現すると、
$$
Y=\begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix}
$$
となり、ブラケット表記では
$$
Y=i(-\ket{0}\bra{1}+\ket{1}\bra{0})
$$
と記述できます。$${Y}$$ゲートの操作を分かりやすいようにBloch球上で表現するとこのようになります。

Hadamardゲート
Hadamardゲートは、$${\ket{0}}$$と$${\ket{1}}$$の重ね合わせ状態を作り出すゲート操作です。
$${H\ket{0}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})=\ket{+}}$$
$${H\ket{1}=\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})=\ket{-}}$$
また、重ね合わせ状態に対してHadamardゲートを与えると、以下のように、それぞれ$${\ket{0}}$$と$${\ket{1}}$$に戻ります。
$${H\ket{+}=H\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})=\ket{0}}$$
$${H\ket{-}=H\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})=\ket{1}}$$
このHadamardゲートを行列で表現すると、
$$
H=\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix}
$$
となり、ブラケット表記では
$$
H=\ket{+}\bra{0}+\ket{-}\bra{1}
$$
と記述できます。また、Hadamardゲートの操作をBloch球上で表現するとこのようになります。

回転ゲート
これまで、単一量子ビットに対して特定の操作を行う量子ゲートを見てきました。では、単一量子ビットに対して任意のゲート操作を実現することはできるでしょうか。つまり、とある量子状態の量子ビットを、任意の軸に関して任意の角度$${\theta}$$だけ回すという操作です。
Bloch球を考えてみましょう。ここで、規格化されたベクトル
$$
{\it {\bf n}}=
\begin{pmatrix}
n_x \\
n_y \\
n_z
\end{pmatrix}
$$
を考えます。そして、この軸に関して量子ビットを$${\theta}$$だけ回転させる単一量子ビットゲートを考えます。するとこの操作は、
$$
R_n(\theta)=e^{-i\frac{\theta}{2}(n_xX+n_yY+n_zZ)}
$$
と表現できます。このゲート操作を回転ゲートと呼びます。さて、この式はどのような意味を持つのかを見ていきましょう。まず、単位ベクトルが
$$
{{\it {\bf n}}}=
\begin{pmatrix} 1 \\
0 \\
0
\end{pmatrix}
$$
の時を考えます。この時、回転ゲートは、
$$
R_x(\theta)=e^{-i\frac{\theta}{2}X}
$$
となります。これがどのような操作に相当するのかを考えます。まず、この式は$${\rm exp}$$の中身が$${X}$$という行列になっています。この時、この指数関数は、結論から答えると
$$
R_x(\theta)=e^{-i\frac{\theta}{2}X}=\cos\frac{\theta}{2}I-\sin\frac{\theta}{2}X=\begin{pmatrix} \cos\frac{\theta}{2} & -i\sin\frac{\theta}{2} \\ -i\sin\frac{\theta}{2} & \cos\frac{\theta}{2} \end{pmatrix}
$$
となり、$${x}$$軸に関しての$${\theta}$$回転を表しています。この式をどのように計算するかについては、最後のおまけをご参照ください。
Bloch球でこのゲート操作を表現するとこのようになります。

また、単位ベクトルが
$$
{{\it {\bf n}}}=\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}
$$
の時、回転ゲートは、
$$
R_y(\theta)=e^{-i\frac{\theta}{2}Y}=\cos\frac{\theta}{2}I-\sin\frac{\theta}{2}Y=\begin{pmatrix} \cos\frac{\theta}{2} & -\sin\frac{\theta}{2} \\ -\sin\frac{\theta}{2} & \cos\frac{\theta}{2} \end{pmatrix}
$$
となります。この操作は、$${y}$$軸に関しての$${\theta}$$回転を表しています。
また、単位ベクトルが
$$
{{\it {\bf n}}}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}
$$
の時、回転ゲートは、
$$
R_z(\theta)=e^{-i\frac{\theta}{2}Z}=\cos\frac{\theta}{2}I-\sin\frac{\theta}{2}Z=\begin{pmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{pmatrix}
$$
となります。この操作は、$${z}$$軸に関しての$${\theta}$$回転を表しています。Bloch球でこの操作を表現するとこのようになります。
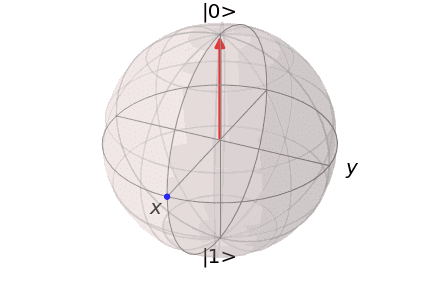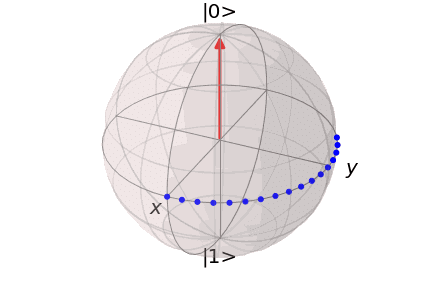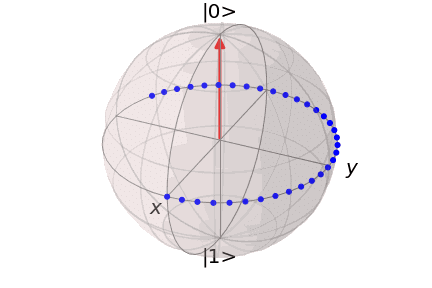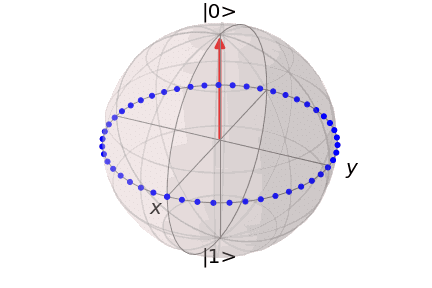
そして、これらの回転ゲートを組み合わせることで、任意の単一量子ビットの回転を実現することが可能になります。
複数量子ビットゲート
複数量子ビットゲートは、複数の量子ビットに対して作用する量子ゲートです。具体的には、以下のような量子回路図で表現されます。
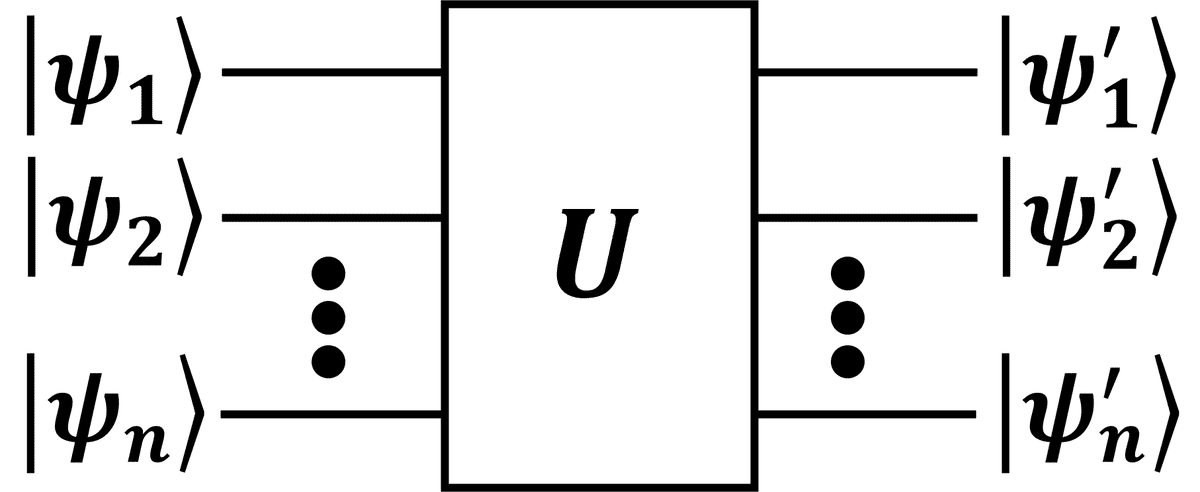
2量子ビットゲート
量子計算では、特に2量子ビットゲートがよく使われます。2量子ビットゲートは、量子回路図で記述するとこのようになります。

$${U}$$の部分が、量子ビットに与えるゲートを示します。この図の場合、この図の場合、$${\ket{\psi_1}\ket{\psi_2}}$$という量子状態の量子ビットが入力され、出力状態は
$$
\ket{\psi_1^\prime}\ket{\psi_2^\prime}=U\ket{\psi_1}\ket{\psi_2}
$$
となります。さて、この2量子ビットゲートは、数学的にどのように記述できるでしょうか。結論から答えると、2量子ビットゲートは、4×4の複素行列で記述されます。今ここで、2個の量子ビット(量子ビット1, 量子ビット2)があるとしましょう。
量子ビット1: $${\ket{\psi_1}=\alpha_1\ket{0}+\beta_1\ket{1}}$$
量子ビット2: $${\ket{\psi_2}=\alpha_2\ket{0}+\beta_2\ket{1}}$$
これらの2量子ビットの量子状態は、それぞれの量子ビットのテンソル積で表現可能であり、
$$
\ket{\psi_1}\otimes\ket{\psi_2}=(\alpha_1\ket{0}+\beta_1\ket{1})\otimes(\alpha_2\ket{0}+\beta_2\ket{1})
$$
$$
=\alpha_1\alpha_2\ket{00}+\alpha_1\beta_2\ket{01}+\beta_1\alpha_2\ket{10}+\beta_1\beta_2\ket{11})
$$
となります。ここで、それぞれの基底は、
$$
\ket{00}=\begin{pmatrix} 1\\ 0\\ 0\\ 0 \end{pmatrix},\, \ket{01}=\begin{pmatrix} 0\\ 1\\ 0\\ 0 \end{pmatrix},\, \ket{10}=\begin{pmatrix} 0\\ 0\\ 1\\ 0 \end{pmatrix},\, \ket{11}=\begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix},\,
$$
$$
\ket{\psi_1}\otimes\ket{\psi_2}=\begin{pmatrix} \alpha_1\alpha_2\\ \alpha_1\beta_2\\ \beta_1\alpha_2\\ \beta_1\beta_2 \end{pmatrix}
$$
つまり、2量子ビットゲートは、4×4の複素行列で記述されます。
CNOTゲート
さて、具体的な2量子ビットゲートを見ていきましょう。最初に紹介する2量子ビットゲートは、CNOTゲートです。CNOTゲートはControlled-NOTゲートの略で、下図のような量子回路図で描かれます。

上側の量子ビットを、制御ビットと呼び、下側の量子ビットを標的ビットと呼びます。CNOTゲートは、制御ビットが$${\ket{1}}$$の時、標的ビットに$${X}$$ゲートを作用させ、制御ビットが$${\ket{0}}$$の時は、何もしないというゲート操作になります。
ブラケット表記を用いると、CNOTゲートは
$$
U_{\rm CNOT}=\ket{0}\bra{0}\otimes I+\ket{1}\bra{1}\otimes X
$$
となります。
さて、行列でCNOTゲートを表現するとどうなるでしょうか。CNOTゲートの働きは、次のように記述できます。
$$
U_{\rm CNOT}\ket{0}\ket{0} = U_{\rm CNOT}\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}=\ket{0}\ket{0}\\ U_{\rm CNOT}\ket{0}\ket{1} = U_{\rm CNOT}\begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}=\ket{0}\ket{1}\\ U_{\rm CNOT}\ket{1}\ket{0} = U_{\rm CNOT}\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}=\ket{1}\ket{1}\\ U_{\rm CNOT}\ket{1}\ket{1} = U_{\rm CNOT}\begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}=\ket{1}\ket{0}
$$
つまり、CNOTゲートは、以下のような4×4の行列で表現されます。
$$
U_{\rm CNOT} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}
$$
エンタングル状態生成
このCNOTゲートを使うと、2つの量子ビットがもつれた状態、つまりエンタングル状態を生成することが可能になります。具体的に見ていきましょう。ここで以下の量子回路を考えます。
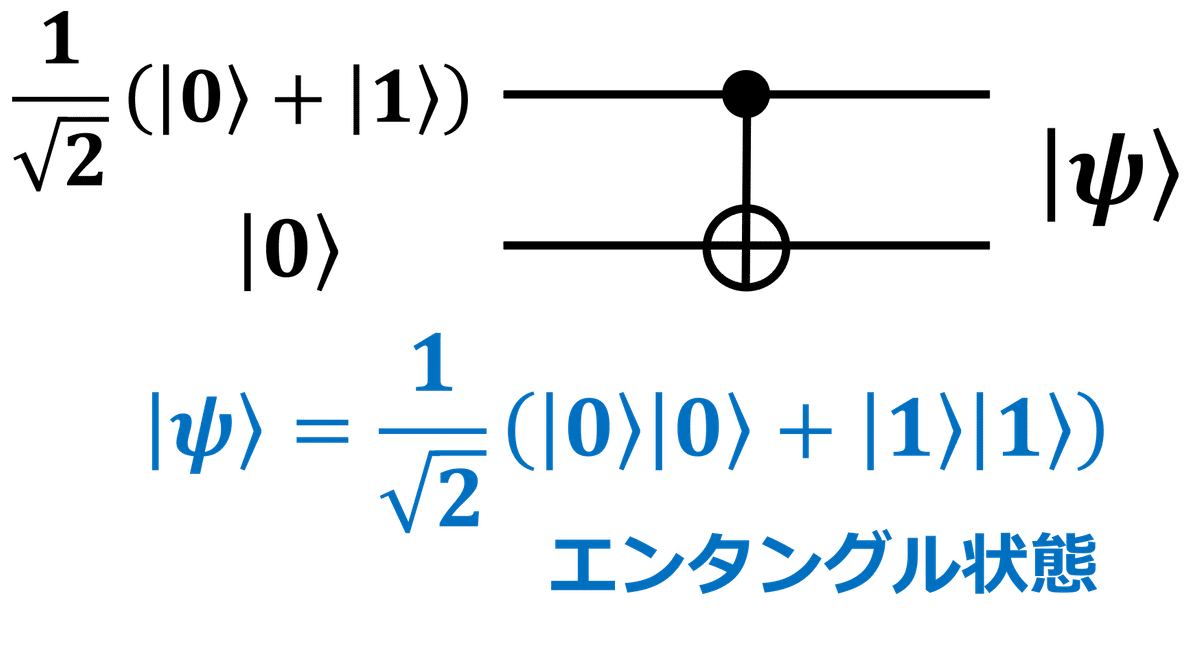
初期状態
まず、2つの量子ビットは初期状態として
$$
\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\ket{0}=\frac{1}{\sqrt{2}}(\ket{0}\ket{0}+\ket{1}\ket{0})
$$
が入力されています。
CNOTゲート
次に、CNOTゲートが作用します。その結果、量子状態は、
$$
\ket{\psi}=\frac{1}{\sqrt{2}}(\ket{0}\ket{0}+\ket{1}\ket{1})
$$
となります。このように、エンタングル状態を生成することが可能になります。
CZゲート (制御Zゲート)
次に紹介するのが、CZゲートです。CZゲートは、Controlled-Zゲートを意味しています。

CZゲートの動作をまとめると、このようになります。

ブラケット表記を用いると、CZゲートは
$$
U_{\rm CZ}=\ket{0}\bra{0}\otimes I+\ket{1}\bra{1}\otimes Z
$$
となります。また、CZゲートの働きは、次のように記述できます。
$$
U_{\rm CZ}\ket{0}\ket{0} = U_{\rm CZ}\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}=\ket{0}\ket{0}\\ U_{\rm CZ}\ket{0}\ket{1} = U_{\rm CZ}\begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}=\ket{0}\ket{1}\\ U_{\rm CZ}\ket{1}\ket{0} = U_{\rm CZ}\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}=\ket{1}\ket{0}\\ U_{\rm CZ}\ket{1}\ket{1} = U_{\rm CZ}\begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \\ -1 \end{pmatrix}=-\ket{1}\ket{1}
$$
つまり、CZゲートは、以下のような4×4の行列で表現されます。
$$
U_{\rm CZ} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}
$$
おまけ
回転ゲートの導出
$$
R_x(\theta)=e^{-i\frac{\theta}{2}X}=\sum_{n}\frac{1}{n!}(-i\frac{\theta}{2}X)^n
$$
$$
=I+(-i\frac{\theta}{2}X)+\frac{1}{2!}(-i\frac{\theta}{2}X)^2+\frac{1}{3!}(-i\frac{\theta}{2}X)^3+\cdots
$$
$$
=I+(-i\frac{\theta}{2})X+\frac{1}{2!}(-i\frac{\theta}{2})^2X^2+\frac{1}{3!}(-i\frac{\theta}{2})^3X^2X+\cdots
$$
ここで$X^2=I$より、
$$
=I+(-i)(\frac{\theta}{2})X+\frac{1}{2!}(-i)^2(\frac{\theta}{2})^2I+\frac{1}{3!}(-i)^3(\frac{\theta}{2})^3X+\cdots
$$
$$
=\sum_{n}\frac{(-i)^{2n}}{2n!}(\frac{\theta}{2})^{2n}I-i\sum_{n}\frac{(-i)^{2n}}{(2n+1)!}(\frac{\theta}{2})^{2n+1}X
$$
$$
=\sum_{n}\frac{(-1)^{n}}{2n!}(\frac{\theta}{2})^{2n}I-i\sum_{n}\frac{(-1)^{n}}{(2n+1)!}(\frac{\theta}{2})^{2n+1}X=\cos\frac{\theta}{2}I-i\sin\frac{\theta}{2}X
$$
CNOTゲートを用いたCZゲートの実装
CZゲートを用いることで、CNOTゲートを実装することができます。CNOTゲートは、
$$
U_{\rm CNOT} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} = \begin{pmatrix} I & O \\ O & X \end{pmatrix}
$$
と表現できます。ここで、$${I}$$は単位行列、$${O}$$はゼロ行列、そして$${X}$$は、$${X}$$ゲートの行列を表しています。
ここで、$${X=HZH}$$という関係式をもいると、
$$
U_{\rm CNOT} = \begin{pmatrix} I & O \\ O & X \end{pmatrix} = \begin{pmatrix} I & O \\ O & HZH \end{pmatrix}= \begin{pmatrix} H & O \\ O & H \end{pmatrix} \begin{pmatrix} I & O \\ O & Z \end{pmatrix} \begin{pmatrix} H & O \\ O & H \end{pmatrix}
$$
となります。つまり、量子回路で表現すると以下のようになることがわかります。

(こちらの記事は、以前Qiitaに投稿した内容の書き直しです。)
