
1つの母平均に関する検定・推定(母分散既知)【超詳細解説】
前提知識はこちらから!
例題
ある工場で生産されている製品は平均重量$${\mu_0=105.0g}$$、標準偏差$${\sigma=1.2g}$$で安定しています。生産ラインの設備が変更されたため、検査員が$${n=10}$$の抜き取り検査を行なったところ、製品平均重量が$${\mu=105.8g}$$でした。
設備変更後の製品の重量はこれまでと異なると言えるかどうか、有意水準5%で検定しなさい。また変更後の重量の区間推定をしなさい。
ただし、設備の変更前後でばらつきは変化しないものとします。
検定
帰無仮説と対立仮説
解説です。
まずは帰無仮説と対立仮説を設定します。
なんでそんな事しなくちゃならんのだ、とツッコミが飛んできそうですが、仮説検定のお決まりの手順みたいなものと考えてください。試験でもこのまま出題されますので、必ずこの手順をマスターしておく必要があります。
帰無仮説というのは、「製品重量がこれまでと変わらない」とする仮定、
対立仮説というのは、「製品重量がこれまでと異なる」とする仮定、
のことです。いちいち帰無仮説と漢字で書くのはメンドクサイので、帰無仮説は記号で$${H_0}$$、対立仮説は$${H_1}$$と書きます。
式で表すと、帰無仮説は
$$
H_0:\mu_0=\mu
$$
対立仮説は
$$
H_1:\mu_0\ne\mu
$$
と表せます。当たり前のことを書いただけですね。
製品重量が変わらないってことは、変更前の平均重量$${\mu_0}$$と変更後の平均重量$${\mu}$$が同じってことなので、$${\mu_0=\mu}$$。これが帰無仮説$${H_0}$$です。
変更前と変更後の重量が異なるってことは、$${\mu_0\ne\mu}$$ですから、これが対立仮説$${H_1}$$です。
有意水準
これはどういう意味かと言うと、どのぐらいの確率で平均重量が異なると判断するかの基準です。変更前の工程から$${n=10}$$を抜き取って、平均値が105.8gになる確率が有意水準(5%)以下なら、これまでと異なると考えましょうって事ですね。
問題をグラフでイメージする事が大切
今回の問題をグラフにするとこんな感じです。
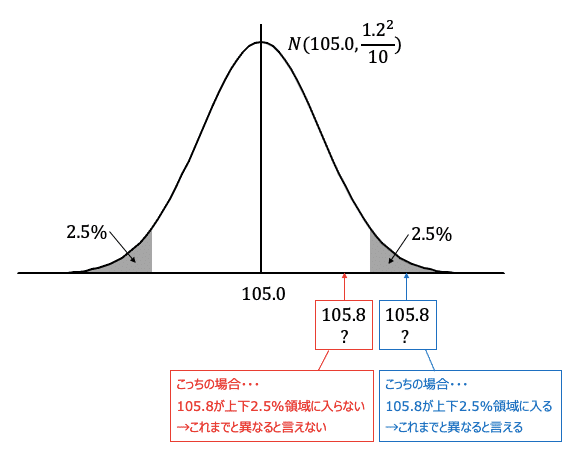
「異なると言えるかどうか」と言われたら、105.0より小さい方に異なる場合も、大きい方に異なる場合もあるので、上下2.5%(合わせて有意水準5%)を考えます。グラフの灰色の部分が上下2.5%領域です。
今回の問題で、変更後の平均重量105.8gがこれまでと異なるかどうかは、$${N(105.0,\cfrac{1.2^2}{10})}$$のグラフにおいて、105.8が2.5%領域に入るか入らないかを見分けることで分かります。
105.8が上下2.5%領域に入れば起こる確率はそこそこ高い→異なると言えない。105.8が上下2.5%領域に入れば、起こる確率がメッチャ低い→これまでと異なると言える
ということですね。
問題を見てこのグラフをイメージできるかどうかが、最重要ポイントです。
逆にこのイメージさえできるようになれば、問題は解けたも同然と言えるでしょう。
慣れないうちは、毎回このグラフを書いて問題を解くことをオススメします。
標準化しよう
先ほどのグラフを標準化して、標準正規分布のとき、105.8がどの値になるのか求めます。
求めたい点を$${u_0}$$とおきましょう。
(標準化することで105.8が$${u_0}$$という値に変化するイメージです)
標準化後のグラフはこんな感じになるはずです。

標準正規分布における上側2.5%点は標準正規分布表から1.96であることが分かりますので、この問題の場合、$${u_0}$$の計算結果が1.96より大きいか小さいかが分かれば良い、ということですね。

「両側5%点が1.96だよ」って事が一目でわかるように記号をつけておきましょう。$${u(0.05)=1.96}$$とします。
かっこの中の0.05が両側5%って意味です。何で$${u}$$やねん!!って思うかもしれませんが、まぁそう置くのが通例だぐらいに思っておいてください笑。
判定結果はどうなる!?
では$${u_0}$$を計算してみましょう。
$$
u_0=\cfrac{\mu-\mu_0}{\sqrt{\cfrac{\sigma^2}{n}}}=\cfrac{105.8-105.0}{\sqrt{\cfrac{1.2^2}{10}}}=2.11
$$
となりました。

$${u_0}$$が1.96よりも大きくなることが分かりました。
式にして書くと、
$$
u_0=2.11>u(0.05)=1.96
$$
ですね。この状態を「有意である」と言います。
そして、$${u_0}$$が$${u(0.05)}$$よりも大きくなったということは、帰無仮説$${H_0:\mu_0=\mu}$$は間違っていて、対立仮説$${H_1:\mu_0\ne\mu}$$が正しいということです。
これを帰無仮説を棄却し、対立仮説を採択する。
と言います。
よって、有意水準5%で製品重量は異なると言える。
が答えですね。
区間推定
区間推定って何??
次に区間推定をしましょう。
今回、設備の変更後$${n=10}$$を抜き取った結果、たまたま105.8という平均値が得られましたが、それはたった1回の抜き取りの結果でしかありません。
もう一回、$${n=10}$$を抜き取って平均値を求めたら、当然違う平均値が出てくるはずです。
なので、たった一回の結果だけを信じて、平均値が105.0から105.8に変化したとは言えないわけですね。
じゃあ、設備変更後の平均値はどの範囲にあると考えられるのか。
これを求めるのが区間推定です。
キーポイントはイメージすること
では、設備変更後のグラフがどうなるか考えてみましょう。
設備変更後の真の平均値は分かりません。しかし、今回の抜き取り結果で平均値は105.8となったので、一旦、平均値が105.8のグラフを考えます。推定に使えるデータはこれしかありませんからね。また、分散は設備変更前後で変わりませんから、そのまま$${\cfrac{1.2^2}{10}}$$です。
そして、有意水準5%で信頼区間を求めるということは、下のグラフのように上下2.5%領域を除いた区間で平均値がどのような値になるかを考えるということです。
要は、今回の抜き取り結果から考えると、この範囲の中に
「設備変更後の真の平均値が存在する可能性が高い」
という意味です。

ここでも標準化
求めたい真の平均値の推定値を$${\hat{\mu}}$$とします。三角帽子のことを「ハット」と読みます。この場合、「ミューハット」です。推定値のことを「ハット」を付けて表すことが多いので、覚えておいてください。
さて、上のグラフを標準化します。
標準正規分布における上下2.5%点は1.96でしたね。標準化後のグラフはこんな感じになるはずです。
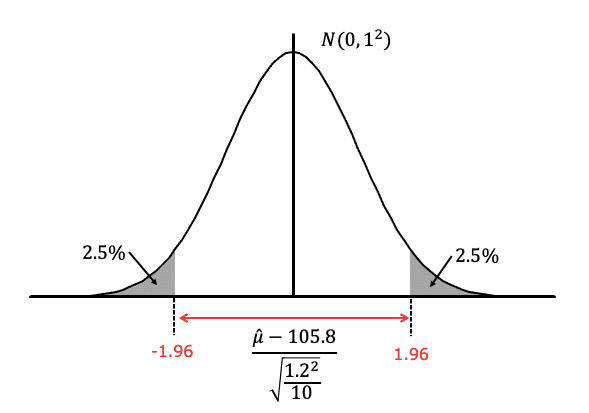
$${N(105.8,\cfrac{1.2^2}{10})}$$における$${\hat\mu}$$は標準化すると、$${\cfrac{105.8-\hat\mu}{\sqrt{\cfrac{1.2^2}{10}}}}$$に変化します。これが、-1.96と1.96の間にあるという形を導く事ができました。
式にすると、
$$
-1.96\leqq{\cfrac{\hat\mu-105.8}{\sqrt{\cfrac{1.2^2}{10}}}}\leqq1.96
$$
です。ここまでできれば、$${\hat\mu}$$を求める事ができそうですね。
計算しましょう。
$$
-1.96\cdot\sqrt{\cfrac{1.2^2}{10}}\leqq\hat\mu-105.8\leqq1.96\cdot\sqrt{\cfrac{1.2^2}{10}}
$$
$$
105.8-1.96\cdot\sqrt{\cfrac{1.2^2}{10}}\leqq\hat\mu\leqq105.8+1.96\cdot\sqrt{\cfrac{1.2^2}{10}}
$$
$$
105.1\leqq\hat\mu\leqq106.5
$$
となって区間推定できました。
信頼区間とは
ちなみに、今回有意水準5%で行なった区間推定の範囲は、95%信頼区間とも呼ばれます。
区間推定の説明で、この区間の中に
「設備変更後の真の平均値が存在する可能性が高い」
と説明しましたが、正しい95%信頼区間の意味は
100回サンプルを取って、100回区間推定をしたら、95回はこの中に真の平均値(母平均と呼びます)を含むだろう、ということです。
逆にいうと、100回中5回は信頼区間の中に母平均がない可能性がある、ということになりますね。
気をつけなければならないのは、
「信頼区間の中に95%の確率で母平均が含まれる」という意味ではありません。
母平均は1つの値(定数)です。1つの信頼区間に対して母平均が95%の確率で含まれると言ってしまうと、母平均の値がころころ変わってしまうという意味になってしまいますよね?これは正しくありません。
よくある間違いですので、気をつけましょう。
以上、母分散既知の母平均に関する検定・推定でした。
他にもQC検定・統計検定などに役立つ解説記事を書いています。
是非ご覧ください。
よかったらスキ・フォローもお願いします!
この記事が気に入ったらサポートをしてみませんか?
