チャンミ勝率の計算

こんにちわ。最近ポケモンの人となりつつあるぴらんです。今回は久々にウマ娘トレーナーになってチャンミの勝率について計算していきます。チャンミの勝率と銘打ちましたが三人対戦のゲームではかなり一般的に成り立ちそうな話なのでウマ娘プレイヤー以外でも見てくれる人いたら嬉しい。

あと、計算面倒そうだったら結果の欄のグラフだけでも見ていってへーと思ってもらいたいです。なにとぞ～～

始めに

ウマ娘では3人が同時に戦うレースを数十回行い、1位を取った回数で報酬や予選突破の可否が決まります。さて、1位を取ることを"勝ち"とする時、平均的なプレイヤーは勝率何％くらいで勝てるのでしょう？

3人のレースなので直観的には平均的なプレイヤーは1/3で勝てそうに思えます。しかし、”レース結果が実力で決まる場合”は中央値のプレイヤーはなんと25%でしか勝てなくなってしまいます。直観とは違って面白いですね。

レース結果が全て実力で決まる場合、勝率は自分より下位の人の割合の2乗。ちょうど真ん中の人なら25％。全て運で決まる場合、勝率は全員33％。つまり運ゲーで損をするのは実力勝負の場合に勝率が33％以上の人に限られ、その割合は(1-1/√3)で約43％しかいないって意外と多いな。

— mee1080 (@mee10801) August 18, 2022

さて、”レース結果が実力で決まる場合”ではない時はどうなるのでしょう？完全に運ゲーなら元ツイートのように全プレイヤー1/3に近づくと期待できますが、その中間はどうなるのでしょうか？またプレイヤーの実力によって1/3に近づく速さが変わったりはするのでしょうか？調べてみました。

計算方法

前提条件

平均$${\mu}$$,標準偏差$${\sigma}$$の正規分布の確率密度関数を$${f(x,\mu,\sigma)}$$と書くことにします。ざっくりいうとちょうどｘになる確率だと思ってください。またそれを積分して得られる累積分布関数を$${F(x,\mu,\sigma)}$$と書くことにします。これはx以下になる確率を表しています。

レースの勝敗を関連する不確定要素としてマッチング運とレースの運があるとし、それぞれが正規分布になるとします。

具体的にはプレイヤーの実力は標準偏差$${\sigma_m}$$での正規分布で分布しており、実力$${x}$$の相手と当たる確率は上で定義した確率密度関数を使って$${f(x,0,\sigma_m)}$$で表せるとします。

また、実力$${x}$$のプレイヤーはレース中の上振れ/下振れにより本来の実力とは異なる力を発揮します。この、レースでの運によって変動した実力をパフォーマンスと呼ぶことにし、パフォーマンス$${p}$$は実力$${x}$$を中心とした正規分布$${f(p,x,\sigma_r)}$$で得られることにします。

レースの勝敗はマッチングした三人の中で最もパフォーマンスが高い人が勝つということにします。

前提まとめ：

$$
マッチング相手の実力の分布：f(x,0,\sigma_m)\\
実力xの人のパフォーマンスの分布：f(p,x,\sigma_r)
$$

勝率に関係する確率の計算

レース勝率を求めるために事前準備としていくつかの確率を先に計算しておきます。

まず対戦相手がパフォーマンス$${p}$$になる確率を求めます。

まずマッチする相手の実力が決まってその後でその実力の人のパフォーマンスが$${p}$$まで上振れる確率を考えます。マッチした相手の実力が$${x}$$になる確率は$${f(x,0,\sigma_m)}$$、そこから$${p}$$まで上振れる確率が$${f(p,x,\sigma_r)=f(p-x,0,\sigma_r)}$$ですので、対戦相手のパフォーマンスの分布は次の式で表せます。

$$
対戦相手のパフォーマンスがpになる確率=\int f(x,0,\sigma_m)f(p-x,0,\sigma_r)dx
$$

これは畳み込みという形式の積分になっており、正規分布同士の畳み込みは平均や分散の和を取った正規分布になり,簡単に計算できるという性質があります。（正規分布の再生性）

今回の場合は平均０同士、分散は$${\sigma_{r}^2}$$と$${\sigma_{m}^2}$$であるため畳み込んだ後に生まれる正規分布の平均は０、分散は$${\sigma_{rm}^2=\sigma_{r}^2+\sigma_{m}^2}$$になります。以上をまとめると次の式になります。

$$
対戦相手のパフォーマンスがpになる確率=f(p,0,\sigma_{rm})
$$

パフォーマンスがちょうど$${p}$$ではなく$${p}$$以下である確率を求めるには積分して累積分布関数にすればよいので$${f}$$を$${F}$$に変えて次になります。

$$
対戦相手のパフォーマンスがp以下になる確率=F(p,0,\sigma_{rm})
$$

次に実力順にプレイヤーを並べた時の順位と実力の数値の関係を調べます。
プレイヤー数によって取りうる数字が変化する順位をそのまま扱うのは面倒なので、プレイヤー数で割った順位率$${n}$$を次で定義します。

$$
n=\frac{プレイヤー数-順位}{プレイヤー数}
$$

これはプレイヤー数に関わらず0%から100%の範囲を動き、最下位は０%一位は100%の値を取ります。意味合いとしては自分より下のプレイヤーの割合を表すような量になっています。

自分より下のプレイヤーの割合は累積分布関数で計算できるので順位率$${n}$$と実力$${x}$$の関係は次のように書けます。

$$
n=F(x,0,\sigma_m)
$$

勝率の導出

自分のパフォーマンスが$${p}$$になった時、自分の勝利条件は対戦相手の2人のパフォーマンスが$${p}$$以下になることです。したがって勝率は以下のようになります。

$$
勝率＝(自分のパフォーマンスがpである確率)\\ \times(対戦相手１のパフォーマンスがp以下である確率) \\ \times (対戦相手２のパフォーマンスがp以下である確率)\\をpの取りうる全パターンについて足す
$$

事前に計算していた通り、自身のパフォーマンスの分布は$${f(p,x,\mu)}$$、相手のパフォーマンスが$${p}$$以下になる確率は$${F(p,0,\sigma_{rm})}$$で計算できるので↑で日本語で書いたものを数式で表すと次のようになります。

$$
勝率＝(自分のパフォーマンスがpである確率)\\ \times(対戦相手１のパフォーマンスがp以下である確率) \\ \times (対戦相手２のパフォーマンスがp以下である確率)\\をpが取りうる全パターンについて足す\\
=\int f(p,x,\sigma_m)\times F^2(p,0,\sigma_{rm}) dp
$$

お疲れ様です。この形まで変形できれば$${f}$$や$${F}$$は正規分布の確率密度関数・累積分布関数として多くのプログラミング言語やエクセルの関数として計算できるのでそれを色んな$${ｐ}$$のパターンについて和を取ることで計算できます。

以上の計算式を用いてpythonを用いて計算をおこない、勝率と実力の相関を表すグラフを作成しました。

また、前節で定義した順位率を用いて順位率と勝率の比較を求めました。最初に紹介したツイートでは勝率と実力の関係式ではなく、勝率が実力の順位率との関係式になっていましたので、そことの比較という意味ではこのように順位率と勝率のグラフを作成した方がわかりやすくなります。

グラフの図示に当たってレースの運ゲー度$${\sigma_r/\sigma_m}$$を定義します。これはプレイヤーの実力のばらつきに比べてレースの上振れによってひっくりかえる実力の幅がどれだけ大きいかを表しており、運ゲー度が高いほど実力の低い人が実力の高い人に勝ちやすくなります。

結果

勝率と実力の関係を調べたグラフは以下のようになりました。

実力と勝率の関係

実力が低いうちは０％だった勝率が、実力が上がるにつれて勝率が上昇し、最終的に勝率100％になる様子が見て取れます。

また特徴的な点として、運ゲー度の違う曲線が勝率1/3の所でほぼ一点で交わっていることが挙げられます。運ゲー度が増すにつれて勝率１/3の点での傾きが緩やかになり、勝率1/3に近くなる実力の範囲が増加します。

平均的なプレイヤーの実力である実力０のところに注目すると運ゲー度が低いうちは25%程度な勝率が運ゲー度を上げると徐々に上がり、勝率1/3に近づくことがわかります。

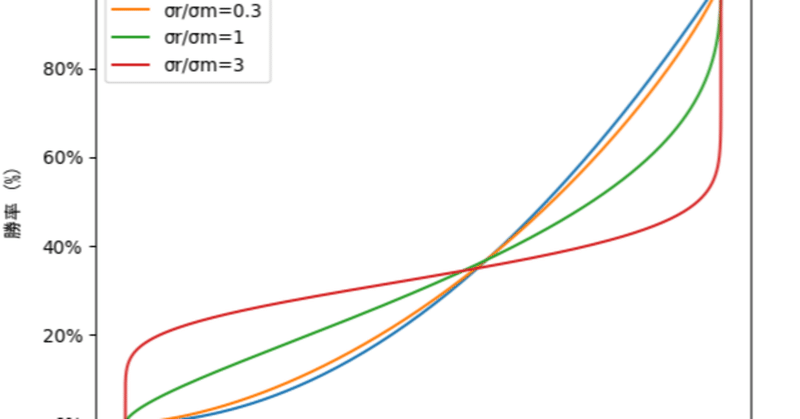
勝率と順位の関係を調べたグラフは以下のようになりました。

勝率と順位率の関係

順位率が上がるほど勝率も上がり、最終的に100％になります。比較の為に最初のツイートで示唆されていた「完全実力勝負では勝率が順位率の2乗に比例」のグラフも書いてあります。

運ゲー度が低いところでは完全実力勝負のグラフに近づく一方で、運ゲー度が上がるにつれてグラフの形が崩れていっているのがわかります。

こちらも実力ー勝率のグラフと同様運ゲー度の異なる曲線がほぼ一点で交わり、運ゲー度が高くなるにつれてそこでの傾きが平らになっていることがわかります。これは運ゲー度が上がるにつれて勝率1/3に近づくことを示しています。

また、順位率５０％付近の平均的プレイヤーは運ゲー度が低いときは実力勝負の時と同じく25%ですが、運ゲー度が上がるにつれて勝率1/3に近づいていることもわかります。

今回定義した運ゲー度は概念上の産物であり、実際のチャンミで運ゲー度がどの程度かはわからないものですが、この「グラフの交点は運ゲー度に関わらず固定」という結論があるため、勝率1/3を超えれるプレイヤー数は約４割だとか勝率1/3付近のプレイヤーは運ゲー化の影響少ないだとかといった性質は実際の運ゲー度がわからなくても成り立つことがわかります。強い！

おわりに

いかがでしたか？

実力勝負だと3人対戦なのに平均的プレイヤーが25%しか勝てないという話から出発して運ゲー要素を取り入れた結果徐々に勝率が1/3に落ち着いていく様子を見ていきました。運ゲーにしていく極限では最終的に1/3になるとわかっていても、その過程でグラフがどう歪んでいって1/3になるかというのはなかなか面白いものがあるんじゃないかと思いました。

あと、個人的にあれ？と思って追加で実験したり証明したけど書ききれなかったこともいくつかあったりするので、同じくあれ？と思った人いたら連絡くれれば「実は考察済で・・・」みたいな話ができるかもしれません。ご連絡はTwitter @pyran19まで～～

ではまた！ぴらーーん