交換読み択のゲーム理論的な考察
こんにちは。計算大好きぴらんです。久しぶりのゲーム理論でポケモンやってみようシリーズになります。
なお、偉そうにムズカシソーなこと言ってますが、ゲーム理論は素人なのでここ間違ってるとかあったらご指摘お願いします(__)
数学苦手な人は計算の章を読み飛ばして考察のところだけでも見ていってもらえると嬉しいです。
要約
ポケモン対戦の交換読み択をゲーム理論のミニマックス戦略を求めるやり方で解析し、交換読みを打つ最適な頻度とその時の利益を計算しました。また、それらに基づいてポケモンの種類ごとにどのような技を持っていることが重要かを調べまとめました。
はじめに
ポケモンで理論派と聞くとダメ計や期待値をガチガチに計算しながら戦うような人を思い浮かべる人も多いかと思います。しかし、雑で大雑把な人間としては細かい数字を出されてもわからない!もっと大雑把な方針や傾向を理論的にやりたいっ!という思いがありました。とにかくポケモン対戦を単純化・簡略化したモデルで何か調べたい!
さて、ポケモンをやっていると一貫性という言葉を聞くことがあります。交代の可能性がある時に現在場にいるポケモンと交換先のポケモンの両方に高い効果を発揮できる技があると一貫性があると呼ばれます。どのような場面やどんなポケモンだと一貫性が大事になるのでしょうか?
というわけでゲーム理論を使って計算を行い、大雑把な傾向に関して何か言えることがないか調べました。
計算
こちら側が有利対面を作ったとして居座りを読んで対面に通る技を選択するか交代を読んで裏のポケモンに通る技を選択するかで2択があるとします。相手の取りうる行動は居座りか交代かの2択であるとします。
こちらと相手の選択に対してそれぞれの場合の利益が次の表のようになってるとします。プラスに大きいほどこちら側の利益が大きく、小さくなったりマイナスになれば相手に有利になります。
$$
\def\arraystretch{1.5}
\begin{array}{c|cc}
& 居座り & 交換 \\ \hline
居座読み & 1& \delta-\alpha \\
交換読み & \epsilon & p-\alpha
\end{array}
$$
$${ε、δ}$$はそれぞれ交代読みと居座りを読み外した相手に打った時の利益であり、一般に小さめな値になります。$${p}$$は交代読みを読み当てた時の利益であり、大きな値になります。
$${\alpha}$$は交代しやすさを表すパラメータであり、交代することによって次ターン以降どれだけの利益を受けられるかを意味します。こちらのポケモンに相手の攻撃が通らない場合はそのまま居座って攻撃するより有利なポケモンに交代した方が次ターン以降大きなダメージを与えられるので$${α}$$は大きくなります。一方、交代せずとも大きなダメージを与えられるような場合やこちら側のAやCが高く交代にリスクが大きい場合は相対的に交代することの利益が小さくなるため$${\alpha}$$が小さくなります。
相手は居座りと交代の利益を比較してこちらの利益が少なくなるように選択します。居座り読みの技を選択する確率を$${x}$$とし、交換読みは$${1-x}$$の確率で選ぶとして相手がどちらを選ぶか考えます。
居座りの利益は$${x+\epsilon(1-x)}$$
交代の利益は$${ (\delta-\alpha)x+(p-\alpha)(1-x)}$$
こちらの利益が少ない方を選ぶので次のようなグラフから青線と赤線の低い方を抜き出したグラフがこちらの利益になります。

つまり↓図の黒線部が$${x}$$毎のこちらの利益になります。
居座りの利益と交代の利益が等しくなる点でこちらの利益が最大化することがわかるので、居座りの利益=交代の利益という方程式を解いて最適な$${x}$$を求めます。

$$
x+(1-x)\epsilon=x(\delta -\alpha)+(1-x)(p-\alpha)\\
(1-\epsilon)x+\epsilon=(\delta-p)x+p-\alpha\\
(1+p-\epsilon-\delta)x=p-\epsilon-\alpha\\
x=\frac{p-\epsilon-\alpha}{1+p-\epsilon-\delta}\\
1-x=\frac{1-\delta+\alpha}{1+p-\epsilon-\delta}\\
$$
したがって$${p,\delta}$$が大きいほど居座り読みの技を多めに打つのが良くなり、$${\epsilon,\alpha}$$が大きいほど交換読みの頻度を上げるのが適切になります。
最適な頻度で選択した時の利益
最適な頻度で技を選択した場合の利益を考えてみます。↑で求めた$${x}$$を居座りの利益の式か交代の利益の式に代入すれば求められます。今回は居座りの利益の式に代入してみましょう。
$$
利益=F=\frac{(1-\epsilon)(p-\epsilon-\alpha)}{1+p-\epsilon-\delta}+\epsilon\\
=\frac{(1-\epsilon)(p-\epsilon-\alpha)+(1+p-\epsilon-\delta)\epsilon}{1+p-\epsilon-\delta}\\
=\frac{p-\epsilon-\alpha-p\epsilon+\epsilon^2+\alpha\epsilon+(1+p-\epsilon-\delta)\epsilon
}
{1+p-\epsilon-\delta}\\
=\frac{p-\alpha+\alpha\epsilon-\delta\epsilon
}
{1+p-\epsilon-\delta}\\
\fallingdotseq \frac1{1+p}\left( p-\alpha+\alpha\epsilon+\frac{\epsilon+\delta}{1+p}\right)\\
利益=P-Q\alpha+\epsilon(Q\alpha+Q^2)+\delta Q^2
$$
最後に$${P=\frac{p}{1+p},Q=\frac1{1+p}}$$と置きました。この時$${P+Q=1}$$であり、それぞれ対面に打つ技と交代読みで打つ技の相対的な強さを表しています。
また、式変形の途中で$${\epsilon,\delta}$$が小さいとして近似を行いました。
また、$${p}$$が少しだけ増減した時にどれくらい利益が変化するかを調べるのに微分を計算しておくと便利です。上の式を微分し、$${\epsilon,\delta}$$を小さいとして無視すると以下のようになります。
$$
\frac{\partial F}{\partial p}=\frac{1}{1+p}-\frac{p-\alpha}{(1+p)^2}=\frac{1+\alpha}{(1+p)^2}=(1+\alpha)Q^2
$$
考察
以上の結果を詳しくみることでポケモンの種類ごとにどんな技を持つと良いのか調べていきましょう。
計算結果の解釈のやり方と具体例
$${\epsilon}$$や$${\delta}$$に掛け算されている係数が大きい場合、それらの変数が少し変わっただけで最終的な利益が大きく動くことになり、それらの変数が表している概念の重要性が大きいことになります。
それでは定義に戻ってそれぞれの変数の意味を振り返っておきます。
$$
\def\arraystretch{1.5}
\begin{array}{c|cc}
& 居座り & 交換 \\ \hline
居座読み & 1& \delta-\alpha \\
交換読み & \epsilon & p-\alpha
\end{array}
$$
対面に普通に攻撃するときの利益を1として、$${\epsilon}$$は交換読みが対面に当たった時の利益、$${\delta}$$は居座り読みの攻撃が交換先に当たった時の利益、$${p}$$は交換読みが交換先に当たった時の利益となっています。
$${\alpha}$$に関しては少しややこしいので定義したところの説明を見返してほしいですが、簡単に言えば交換をどれだけしやすいかを表しているパラメータになっています。
例えば最終的な利益が$${0.1\epsilon+100\delta}$$だった場合、ほとんど$${\delta}$$だけで利益が決まってしまい、$${\epsilon}$$の大小は重要でないことがわかります。
具体的には$${\epsilon,\delta}$$がともに0.5だと最終的な利益は50.05であり、そこから$${\epsilon,\delta}$$をそれぞれ0.1ずつ増減させて$${(\epsilon,\delta)=(0.4,0.6)}$$で計算しても60.04となり$${\epsilon}$$の減少が効いてないことがわかります。
これを$${\epsilon,\delta}$$の意味を思い出して解釈しなおしてみると、居座り読みで打つ技が読み外しても裏にちゃんと一貫していることの重要性が非常に高く、一方で交換読みが対面に通ってる重要性が非常に低い状況を表していると解釈できます。
$${p}$$に関しては$${何か\times p}$$の形になっていないので$${p}$$の係数という言い方はできないのですが、代わりに$${p}$$の微分を係数の代わりに使えます。
計算結果への適用
以上の例を踏まえて実際の計算結果がどのような意味を持っているか考えていきます。

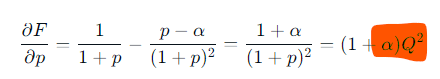
$${\alpha}$$が含まれているのは$${p}$$微分の項と$${\epsilon}$$の係数です。
つまり$${\alpha}$$が大きくなると「交換読みの居座りへの通りの良さ」と「交換詠みの交換先への通りの良さ」の重要性が上がります。
さらに詳しく見ると$${\alpha}$$がかかっている項が$${Q^2}$$と$${Q}$$と異なっているので$${Q}$$の大きさ次第でどちらが重要になってくるかが異なってきます。$${Q}$$が大きいと二乗で入ってきている交換読みの交換先への通りの良さが相対的に重要になり、$${Q}$$が小さいと$${Q}$$の一乗が係数になっている$${\epsilon}$$の重要性が上がります。

$${δ}$$の係数は唯一αが含まれていない項です。したがって相対的に重要性が上がるのはαが低い時になります。つまり居座りに向けて打つ技が裏にも通っている必要があるのは、相手の交換を誘いにくく対面的な性質が強いポケモンになります。
どんなポケモンにどんな技が重要になるか
αの低いポケモン、つまり弱点の少なさや火力の高さにより交代を誘いにくい対面ポケモンでは対面に向けて打つ技の一貫性が重要になります。交代を誘いにくいので素直に対面向けの技を打つことが多くなり、交代に対する対策も対面に向けて撃った技で行うことが多くなるのが原因と考えられます。
受けポケモンは耐久の高さにより役割対象に交代を強制しやすい一方で交代読みの技の火力が低くなりがちで、$${\alpha}$$が高く$${p}$$や$${Q}$$が小さいポケモンと考えることができます。このようなポケモンは交代読みで打つ技が居座りに対しても通りが良いことが重要になります。
受け切られてる相手に居座っても意味がない上に火力が無い関係で交代しやすいので相手視点で交代安定になるため結局交換読みの技をばかり打つことになり、対面に圧力をかける方法も交換読みで行う必要が出てくるためだと考えられます。
実際、こういう受けポケモンから一撃技や催眠技のように対面にも一定の効果のある技を交代読みでぶっぱされると相手にしていて嫌かと思います。
弱点と耐性が多く、火力の高い交換読みを持つようなサイクル向けのポケモンは有利対面に交代を強制しやすく交代読みの火力も高いので、$${\alpha}$$や$${p}$$の高いポケモンと言えます。計算結果を参照すると、このようなポケモンは交代読みをしっかり交代先へ読み当てた時のリターンが大きい事が重要であることがわかります。
交換させる圧力が強く交換読みが重要になるのですが、受けポケの場合と違って交換読みの火力の高さゆえに相手の交換がやや少なくなり、それに合わせて交換読みの頻度が下がり、対面には居座り読みで、交換先には交換読みで、と技毎に分担して圧力をかけていくイメージになるかと思います。
まとめ
有利対面からの交換読みを2択×2択のゲームととらえてミニマックス戦略を求めることで、ポケモンの種類別に必要な技の性質を調べました。
試合中の段階では交換先のポケモンに居座り読みや交換読みが刺さっているほど居座り読みの頻度を上げるのがよく、交換圧が強かったり対面のポケモンに交換読みで十分なダメージを与えられる状況では交換読みの頻度を高くするのが良くなります。
構築段階では交換を誘いにくい対面ポケモンは居座り読みが裏にも通りが良いことが重要になります。
受けポケモンでは交換読みが対面にも圧力かけられる技であることが重要になります。
多弱点多耐性高火力のサイクルポケモンでは交換読みが交換先にしっかり刺さっていることが重要になります。
おわりに
いかがでしたか?実際の対戦と比べるとめちゃくちゃ単純化したモデルからのスタートでしたが、意外と実際の対戦と関係のある結果が出てきたのではないかと思います。対面ポケモンに通りの良い技を要求されたり、サイクル適正の高いポケモンでは交代読みで弱点を突いていく必要性が高かったりなどは実戦での感覚にある程度近いものがあるんじゃないかと思います。
かなり単純化したモデルなのであくまで一般論に留まりますが、机上論でも意外と色んな事がわかるんだよ~というわかってもらえれば嬉しいです。
では次の記事でお会いしましょう
この記事が気に入ったらサポートをしてみませんか?
