「第一回ルールでっち上げ大会」延長戦チャレンジ日記
この記事は、ペンパアドベントカレンダー2019A2の19日目の記事です。
さっき企画を思いついたので面白いかはわからないがとりあえずフォームを作ったhttps://t.co/ayFZN2bRTC
— ひこうき (@flight_float) November 14, 2019
先月、「ルールでっち上げ大会」という企画が開催されました。
第一回ルールでっち上げ大会 投稿作発表part1
第一回ルールでっち上げ大会 投稿作発表part2
ひとりで「ルールでっち上げ大会」の延長戦をおこない、過程を残す意図で記録を残していきます。
本選でルールを絞りつくしたあとなので、うまいルールをでっち上げられるかどうかはわかりませんが、後先考えず書いていきます。完成した問題だけを見たいかたはこちら。
第一回ルールでっち上げ大会のお題はこんな盤面でした。

1日目
領域に分かれた盤面ということで、ぱずぷれのパズル一覧から「領域+黒マス系」を見てみる。
タイルペイント
のりのり
ぬりめいず
LITS
島国
ストストーン
ペイントエリア
チョコナ
アクアプレース
「のりのり」と「ストストーン」は投稿されてたから、残りから選ぶとなると……「島国」あたりだろうか。
島国のルール
1. 太線で区切られたところ(海域)すべてに、以下のルールに従って黒マスのかたまり(国)を配置します。
2. タテヨコにつながった黒マスのカタマリを1つの国とします。1つの海域には、必ず1つの国が入ります。
3. 海域内の数字は、国のマスの数を表します。数字のない海域では、国のマスの数は分かりませんが、0にはなりません。
4. 異なる海域にある国どうしは、辺を共有しません。角で接するのはかまいません。
5. 辺を共有する海域どうしでは、国の大きさは必ず異なります。
そのままのルールだと別解だらけだから、強めの制約を加えないと唯一解にならなさそうだ。
「隣接する部屋では、黒マスが同じ個数でも一つ違いでもダメ」とか……ええと、ちょっと待てよ……
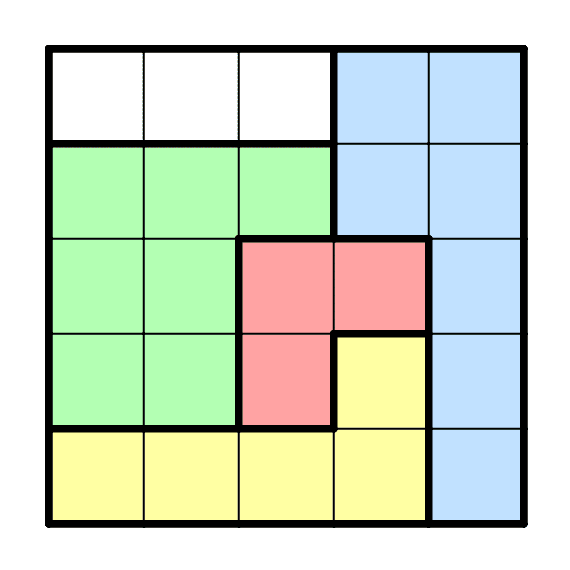
色を付けた4つの部屋が、すべて互いに隣り合っている。だから、ひとつ違い禁止ルールだと、この4部屋だけで、最低でも1+3+5+7=16個の黒マスが必要だ。しかしだ‥‥
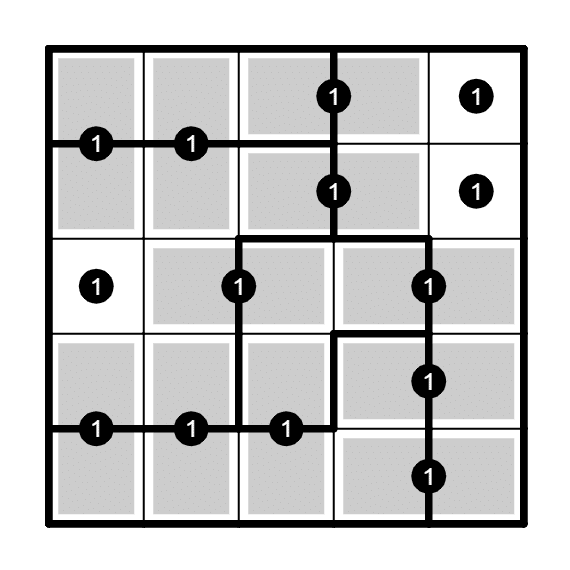
太線を挟んで黒マスが隣接しないから、盤面に入る黒マスは14個が限界だ。ひとつ違いルールは無理だ。しかし14個が限界かぁ……。
※もし15個が限界だったら、「各ブロックに3個ずつ黒マスが入る」や「ブロックに入る黒マスの個数はすべて異なる」というルールを試していたところ。限界ギリギリを目指すルールだと、理詰めの唯一解になりやすい。
「島国」のルール「異なる部屋の黒マスは縦横に隣接禁」を「異なる部屋の黒マスはタテヨコナナメに隣接禁」に変えたらどうだろう。
ええと……考えるより試しに解いたほうが速そうだな……。どうだろう……。
いま試そうとしているルール
「特殊ルール追加島国。異なる部屋の黒マスは、ナナメに隣接してもいけません」

全検の途中だけど、別解出た。惜しい感じがする。ちょっとルール変えたらたぶんいけるだろう。
実際、「各部屋に2つずつ黒マスが入る」とすれば唯一解になる(第一回ルールでっち上げ大会投稿作のNo.6)
黒マスを全部で10コ入れるルールにして、逆になにか制約を強めれば、バランスが取れて唯一解になりそうだ。黒マスを全部で10コというのは、いろんなルールと相性がいい。各列に2コずつ黒マスが入り、各ブロックに0~4コ入るとか。各ブロックに2コずつ黒マスが入り、各列に0~4コ入るとか。
※「各列各ブロックに2コずつ黒マスが入る」を選択肢に入れてないのは、本選で既にさんざん試したルールだから。
とりあえず、唯一解になるか試してみよう。
いま試そうとしているルール
・各列に2つ黒マスが入る
・部屋に入る黒マスの個数は、すべての部屋で異なる
・ひとつの部屋内で黒マスはタテヨコにつながる
・黒マスは太線をまたいでタテヨコに隣接しない
(太線をまたいでナナメに隣接してもいいかどうかは、様子をみて考える)
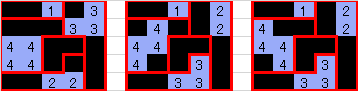
※自分が解くときのクセで、白黒の配色が逆転している。
別解が出た。たぶん3解。惜しい。
別解盤面を観察すると、白マスがギリギリ分断されている。だから、白マスにひとつながりルールを付け加えて、代わりに何か制約を弱めれば唯一解になりそうだ……これは後で試すとして、先に「各ブロックに2個黒マスが入り、各列に入る黒マスの個数が異なる」のほうを検証してみる。
いま試そうとしているルール
・各部屋に2つ黒マスが入る
・タテ列に入る黒マスの個数は、すべてのタテ列で異なる(ヨコも同様)
・ひとつの部屋内で黒マスはタテヨコにつながる
・黒マスは太線をまたいで隣接しない
(黒マスナナメ隣接禁を足すかどうかは、様子をみて考える)
あっさりダメだった。白マスひとつながりのほうを試してみるか。
いま試そうとしているルール
・白マスは全体でひとつながりになる
・各列に2つ黒マスが入る
・部屋に入る黒マスの個数はすべての部屋で異なる(0コでも可)
・ひとつの部屋内で黒マスはタテヨコにつながる
・黒マスは太線をまたいで隣接しない
※このままだと破綻するので、細字のルールをどこか弱める
「白マスひとつながり」と「ひとつの部屋内で黒マスひとつながり」の組合せ、「へやブロ」で見たことある(※JZdC2013ラウンド3など)。好きなルールなので、ここは動かしたくない。
「すべての部屋で黒マスの個数が異なる」は制約が強すぎるかもしれない。ここは「隣接する部屋で黒マスの個数が異なる」くらいに弱めてもいい。
ごちゃごちゃ考える前に、とりあえず試してみるか。
・
・
・
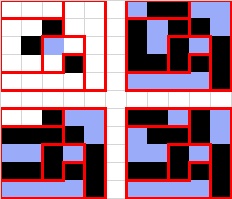
白マスがひとつながりになる島国
※相変わらず白黒逆転して作図している
別解出た。中央が黒マスになるパターンが丸々残っていて、唯一解までは遠そう。
「へやブロ」の要素が加わってるわけだし、三部屋横断禁止ルールも追加しちゃっていいかもしれないな……。もっかい検証してみよう。
いま試そうとしているルール
・特殊ルール追加のへやブロ。隣接する部屋では黒マスの個数が一致しない。どの部屋にも1コ以上の黒マスが入る。
これは破綻するようだ。むぅ……。
検証してみた感じ、白マスが縦横に長く続きがちだった。白マスの長さを制限したりするといいかもしれない。「追加ルールつき定番パズル」で追加ルールをふたつ以上というのは、美学に反するが……。
いま試そうとしているルール
・特殊ルール追加の島国
・白マスはタテヨコにひとつながりになる
・タテヨコに一直線につながる白マスのマス数は、最大でもNマス
ダメだった。破綻。
「白マスひとつながり」と「ひとつの部屋内で黒マスひとつながり」と「太線をまたいで黒マス隣接禁」の組合せで何か完成させたいが……。
……「黒マスはタテヨコナナメにひとつながり」なんてどうだろう。
良くないルールだ。ぜひやろう。
延長戦チャレンジ2日目につづく・・・
2日目
寝てる間に、一個ルールを思いついた。「白マスの個数に関しても、隣接する部屋では同じにならない」という追加ルールつき島国。
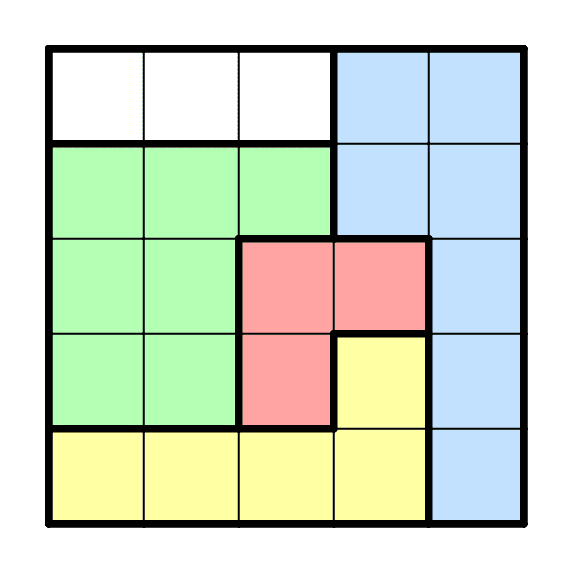
右下の4部屋はすべて互いに隣接している。隣接する部屋で黒マスも白マスも個数が異なるとなると、黒マスが最低でも1+2+3+4=10個、白マスも1+2+3+4=10個必要なわけで、ギリギリ収まる。しかし、これは検証が大変だ……。後回しにしよう。
他にも2,3個のルールを思いついたけど、まずは1日目の続きからいこう。
1日目の終わりに話してたルール
・黒マスはタテヨコナナメにひとつながり
・白マスはタテヨコにひとつながり
似た性質をもつパズルに「しろまるくろまる」がある。
しろまるくろまるのルール
・白マスも黒マスもタテヨコにひとつながり
・白マスも黒マスも2×2禁
「しろまるくろまる」には、外周定理とよばれる定理がある。「同じ色のマスが外周沿いにひとつながりになる」という定理なのだが……

実は、ルールを弱めて、「片方の色は角でも接触可」に変えても、外周定理が成り立つ。

証明
解答盤面では、黒マスが角でしか接触していない箇所があるが、黒マスを少し膨張させると、しっかりと連結される[下図参照]。
しろまるくろまると同様に「白マスも黒マスもひとつながり」になるので、しろまるくろまると同様に外周定理が言える。

外周定理、少し気付きにくい。なおかつ強すぎる定理なので、あまりよろしくないルールだ。制約が強くて解がしぼられてるから、、、ちょっとルールを足したら唯一解になりそうだ。
いま試そうとしているルール
ベースとなるルール
・黒マスはタテヨコナナメにひとつながり
・白マスはタテヨコにひとつながり
(白黒は入れ替わるかも)
追加ルールの候補(一部)
・各列にNコずつ黒マスが入る
・各列に入る黒マスの個数はすべて異なる
・各ブロックにNコずつ黒マスが入る
・各ブロックに入る黒マスの個数はすべて異なる
・隣接するブロックに入る黒マスの個数が異なる
・黒マスは縦横に隣接しない
・黒マスは太線をはさんで隣接しない
・ひとつの部屋の中で黒マスがひとつながりになる
・黒マスは1×Nの長方形になる
・黒マスはNマスずつのカタマリになる
・黒マスは2×2マス以上のカタマリにならない
・黒マスはNマス以上一直線に連続しない
・黒マスがNマス以上のカタマリを作ってはいけない
白マスについても同様。これらのルールをあれこれ入れ替えて、唯一解を目指してみる。
・
・
・
一個できた。
・各部屋に3つずつ黒マスを入れる
・ひとつの部屋の中で黒マスがタテヨコにひとつながりになる
・黒マスは全体でタテヨコにひとつながりになる
・白マスは全体でタテヨコナナメにひとつながりになる
ぱずぷれで解く
あまり良いルールではないが、まぁいいだろう。
・
・
・
もういっこできた。
・各列各ブロックに2つずつ黒マスを入れる
・黒マスが太線をはさんで隣接してはいけない
・黒マスはタテヨコナナメにひとつながりになる
ぱずぷれで解く
白マスのひとつながりルールは外した。やっぱり外周の制約が強すぎる。
シンプルなルールなので、本選で思いつきたかったな。
・
・
・
もういっこ。
特殊ルール追加へやわけ。どの部屋にも黒マスが1つずつ入り、黒マスはナナメにひとつながりになる。
ぱずぷれで解く
これはダメなルール。追加ルールがふたつあるのが美学に反する。それに、ナナメにひとつながりってルールは、偶奇性にもてあそばれている感じがする。
延長戦チャレンジ3日目につづく・・・
3日目
2日目に引き続き、「タテヨコナナメにひとつながり」の路線で考えていこう。
・
・
・
できた。
スクリン×ぬりぼう。
どの部屋にも長方形がひとつずつ入る。スクリンのように、長方形が角でつながってひとつのループを作る。太線をまたいで長方形を置くことはできない。同じ面積の長方形は角で接してはいけない。
ぱずぷれで解く
同じ面積の隣接禁が一か所でしか使われていないのが綺麗じゃないな……。蛇足ルールなのが見え見えだ。
スクリンは、長方形を角でつなげてループを作るパズルだけど、これを辺でつなげるパズルに変えると、稲葉のパズル研究室の「アクロスループ」になる。
アクロスループのルール
1:太線で区切られた全ての部屋の中に、その部屋を「横切る」1×Nマスのブロックを配置する。(つまり、ある辺から反対側の辺まで塗る。)
2:どのブロックも他のちょうど二つのブロックと接するようにし、全体が縦横でつながった一つのループになるようにする。
稲葉のパズル研究室より
アクロスループで唯一解にならないのは本選のときに検証済みだが、長方形以外の形も許したらどうだろう。
試してみたルール
・すべての部屋に、トリオミノ(3マスつながった黒マス)をひとつずつ入れる
・どのトリオミノも、ふたつのトリオミノと辺で隣接して、全体でひとつのループになる
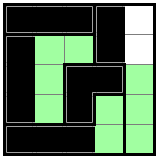
2解だけ残った。蛇足ルールを追加して完成。
・すべての部屋に、トリオミノ(3マスつながった黒マス)をひとつずつ入れる
・どのトリオミノも、ふたつのトリオミノと辺で隣接して、全体でひとつのループになる
・向きも形も同じトリオミノが隣接してはいけない。
ぱずぷれで解く
トリオミノを辺でつなげたけど、角でつなげてループを作るパズルに変えると、稲葉のパズル研究室の「トリオミノループ」になる。この路線も調べてみようか。
トリオミノループのルール
1: あらかじめ塗られているマスをヒントに、盤面にいくつかのトリオミノ(三つの正方形が縦横でつながった図形)を配置する。
2: どのトリオミノも他の二つのトリオミノとそれぞれ一点で接するようにし、全体で一つのループになるようにする。
稲葉のパズル研究室より
ループを作るには盤面が狭すぎるだろうから、「タテヨコナナメにひとつながり」程度でもいいかもな。
いま試そうとしているルール
・トリオミノ(3つつながった黒マス)をいくつか入れる
・トリオミノは角でつながって全体でひとつながりになる
+追加ルール(黒マスを発生させるルール)
むぅ、「各部屋に3マス入る」とすると一瞬で破綻するんだよなぁ……。他にいいルールはないものか……。
部屋に3マスずつだと過多……2つずつだと少ない……各部屋にカタマリがふたつずつ入るようにするか……破綻……全部トリオミノだとキツいか……2マスだと……いやこれは本選で投稿されていたルールだ……2マスと3マスのように面積に幅をもたせれば……なかなかうまくいかないな……各部屋に二種類入るようにして……2と4……1と3…………追加ルールを入れて……
できた。
・いくつかのマスを黒く塗る
・黒マスが縦横につながったカタマリの面積は、1か3のどちらかになる(面積3の黒マスのカタマリを、トリオミノと呼ぶ)
・どの部屋にも、ちょうど1個の「面積1の黒マスのカタマリ」が入る
・どの部屋にも、ちょうど1個のトリオミノ(の一部)が入る
・同じ面積の黒マスのカタマリが角で隣接してはいけない
ぱずぷれで解く
ごっちゃりしてるけど、割と好みのパズルに仕上がった。3マスと1マスがテーマになったパズルといえば、稲葉のパズル研究室の「サントイッチ」がある。明日はその路線から探してみるか。
サントイッチのルール
1:パズル面を壁で仕切り、三マス、または一マスのブロックに分割する。
このとき一マスブロック同士は辺で接しないようにする。
2:三マスのブロック内には必ず数字が一つ入る。
数字はそのブロックが辺で接している一マスのブロックの個数を表す。
稲葉のパズル研究室より
延長戦チャレンジ4日目につづく・・・
4日目
できた。
盤面を面積1または3のブロックに分割する。分割線の一部は最初から盤面に入っている。向きも形も同じブロックがタテヨコナナメに隣接してはいけない。
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jY+7TgQxDEX7fEZqF7aTETtpeVSIgodWKIoQBR8AiCbR/vvcWB6YEnlzdHT3rjf5/vx5//qgZQ4Tk2ASs508P6HOGNNCjRrJjsQWRn8so7+V2i7UX/70qQzwwSjGV+OdUY3PqFJPxhsjG+/t29sy4ppJOMWi+DPWg+OCrO64Lot7IhHPBX3xviBXzxV58n7Cnszegf/+Fq6eK/br6j7zfQ887Z314KdD/wp+guM9Z3vVtTGDlxDq3O2z/M/aBg==
最初は、面積1のブロックがタテヨコに隣接してはいけないというルールで試した。制約が弱かったのでナナメも禁止してみて、それでも唯一解にならなかったから、面積3のブロックにも隣接禁を追加してみた。結果的にシンプルなルールに仕上がったと思う。
面積1と3が対等に扱われているシンプルなルールになったせいで、逆に「1と3のみ」というのが恣意的に見えてしまう。
「面積3以下のブロックに分割する」の方針で試してみよう。
いま試そうとしているルール
盤面を面積3以下のブロックに分割する。
同じ面積の隣接禁とか、同じ形の隣接禁とか、そういう追加ルールで唯一解にしたい。
追加ルールの選択肢が多いから、たぶんいけるだろ。
・
・
・
むぅ、意外にうまくいかないな……。
・
・
・
試してみたルール
・面積4以下のブロックに分割する
・分割線が十字になってはいけない
・同じ面積のブロックは縦横に隣接しない
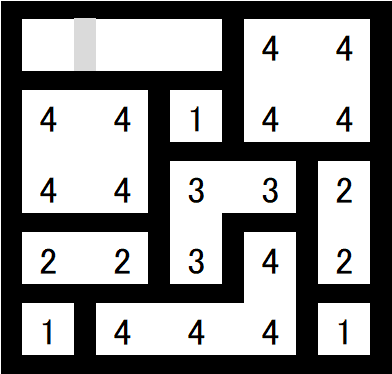
惜しくも唯一解にならなかった。惜しいけど、自然なルールで唯一解にするのも難しそうだ。
あきらめて別のルールを試してみる。
・
・
・
「面積3以下で分割」「同じ形のブロックはタテヨコ(ナナメ)に隣接しない」はダメだった。
・
・
・
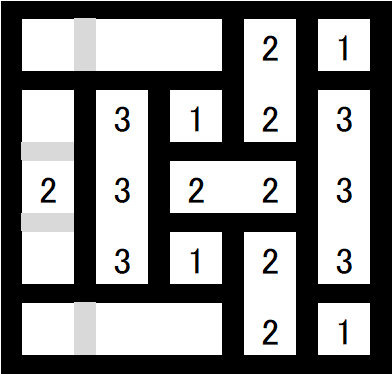
「面積3以下の長方形に分割」「向きも面積も同じ長方形は隣接禁止」を試した図。上下対称形で残っちゃってるから、どうやっても唯一解にはならない。
延長戦チャレンジ5日目につづく・・・
5日目
2日目の最初にふれた、「白マスの個数に関しても、隣接する部屋では同じにならない」の路線でいってみる。
「隣接する部屋では同じにならない」といわず、いっそのこと「全部の部屋で、黒マスの個数も白マスの個数も異なる」としてみよう。
さらに、各部屋に少なくともひとつ黒マスが入るルールも入れる。成立するギリギリのルールなので唯一解になりやすいだろう。
いま試そうとしているルール
・いくつかのマスを黒く塗る
・どの部屋にも少なくともひとつ黒マスが入る
・盤面全体で、黒マスの個数が同じ部屋ができてはいけない
・盤面全体で、白マスの個数が同じ部屋ができてはいけない
+なにか追加ルール
しろまるくろまるだと別解が出るか……。しろまるくろまる以上に強いルールが必要なのだな……。そんな強いルールなかなかないぞ……。
「黒マスは2×2禁でひとつながり」「黒マスは盤面全体で点対称」ですら別解が出るか……。冗談のつもりで試した激強制約ルールだったのだが……。
・
・
・
できた。
・盤面のいくつかのマスを黒く塗る
・どの部屋にも黒マスが少なくとも1コ入る
・黒マスは「交差のないループの内側」の形になる
・黒マスも白マスも、ひとつの部屋のなかでひとつながりになっている
・黒マスも白マスも、2×2以上のカタマリになってはいけない
・盤面全体でみたとき、黒マスの個数が同じ部屋があってはいけないし、白マスの個数が同じ部屋があってもいけない
ぱずぷれで解く
強いルールてんこもり。ここまでしないと唯一解にならない盤面だったっけ……?
※追記
部屋に白マスが存在しなくてもよいルールなのだが、「部屋のなかで白マスがひとつながり」というルールとの相性が悪い。
日本語でルールを表現しづらいという理由により、結局ボツにしたルール。
「黒マスも白マスも、ひとつの部屋のなかでひとつながりになっている」というルールを使ったが、このルールは「各部屋をふたつにわける」というルールと非常に似ている。

せっかくだし、次は「各部屋をふたつにわける」の方針で考えてみよう。
……その前に、ちょっと思いついたことがあるので、別のルールを試してみる。
・
・
・
ダメだった。そしてメチャクチャ検証がつらかった。
試していたルール
・タテヨコナナメに分割線を引いて、盤面をブロックに分割する
・各ブロックの面積は1以上2以下
追加ルール案1『どのブロックも四角形で、同じ形のブロックは隣接禁』
追加ルール案2『同じ面積のブロックは隣接禁』
制約の強さ的にはちょうどいいと思ったんだがなぁ……。残念。
話を戻して「各部屋をふたつに分ける」の方針で考えよう。
……の前に、少し試しておきたいことがある。
本選のときに、唯一解にならずにボツにしたルールがあるのだが、あれに追加ルールを付け加えて唯一解にさせてあげたい。
ボツにしたルール1
・すべてのマスを通る交差可能ループをひとつつくる
・どの部屋にも右折するマスと左折するマスがある
シンプルにして深遠なルール。確か二解だったと思う。
性質の近いパズルに、稲葉のパズル研究室の「メビウスバンド」がある。
よい追加ルールを加えてあげて理詰め問に昇華させてあげたい。
・
・
・
いつのまにか別のルールが完成してた。
・縦横に線を引いて、ループをふたつ作る
・異なるループどうしでのみ、線が立体交差することができる
・どの部屋にも「ループAのみが通るマス」と「ループBのみが通るマス」の両方がある
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jY+7TgQxDEX7fEZqF7aTETtpeVSIgodWKIoQBR8AiCbR/vvcWB6YEnlzdHT3rjf5/vx5//qgZQ4Tk2ASs508P6HOGNNCjRIpKo7EFkZ/LKO/ldou1F/+9KkM8MEoxlfjnVGNz6hST8YbIxvv7dvbMuKaSTjFovgz1oPjgqzuuC6LeyIRzwV98b4gV88VefJ+wp7M3oH//hauniv26+o+830PPO2d9eCnQ/8KfoLjPWd71bUxg5cQ6tzts/zP2gY=
シンプル。満足。理詰めで解けるような解けないような、不思議な問題になった。最初「異なるループどうしでのみ立体交差可能で、すべてのマスを通り、どちらのループも全部屋を通過する」というルールで検証してしまったが、奇数×奇数なので無理な話だった。そういうこともある。
延長戦チャレンジ6日目につづく・・・
6日目
昨日のルールを考え直してたら、いっこできた。
・縦横に線を引いて、ループをふたつ作る
・すべてのマスに線が通る
・線は交差することができる(自己交差でも可)
・どの部屋にも「ループAのみが通るマス」と「ループBのみが通るマス」の両方がある
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jY+7TgQxDEX7fEZqF7aTETtpeVSIgodWKIoQBR8AiCbR/vvcWB6YEnlzdHT3rjf5/vx5//qgZQ4Tk2ASs508P6HOGNNCjRIpKo7EFkZ/LKO/ldou1F/+9KkM8MEoxlfjnVGNz6hST8YbIxvv7dvbMuKaSTjFovgz1oPjgqzuuC6LeyIRzwV98b4gV88VefJ+wp7M3oH//hauniv26+o+830PPO2d9eCnQ/8KfoLjPWd71bUxg5cQ6tzts/zP2gY=
こういう、対照的なルールででっち上げられると嬉しい。
「ひとつルールを弱めて、ひとつルールを強める」というのが、ルールでっち上げの基本。
今日はこのへんにしておく。明日も交差ありループから検証をはじめたい。
延長戦チャレンジ7日目につづく・・・
7日目
交差ありループの可能性をさぐる前に、ちょっと寄り道。
本選で唯一解にできずにボツにした、未練のあるルールがある。
ボツにしたルール2
・タテヨコナナメに線を引いて、始点と終点をもつ一本の線をつくる
・線が交差や枝分かれをしてはいけない
・すべてのマスに線が通る
・ひとつの部屋を連続して3マス以上通ることはできない
+なにか追加ルールを加えて唯一解にしたい
始点と終点が初手で決まる、というネタをやりたいだけのルールなのだが、本選の締切最終日に一日粘っても唯一解にできなかった。こいつに挑戦する。
・
・
・
(大量のルールを試している)
・
・
・
(大量のルールを試している)
・
・
・
(大量のルールを試している)
・
・
・
できた。
・タテヨコナナメに線を引いて、始点と終点をもつ一本の線をつくる
・線が交差や枝分かれをしてはいけない
・すべてのマスに線が通る
・ひとつの部屋を連続して3マス以上通ることはできない
・どの部屋にも45度の急カーブがちょうど1マスだけある
・2連続で45度の急カーブをしてはできない
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jY+7TgQxDEX7fEZqF7aTETtpeVSIgodWKIoQBR8AiCbR/vvcWB6YEnlzdHT3rjf5/vx5//qgZQ4Tk2ASs508P6HOGNNCjRIpKo7EFkZ/LKO/ldou1F/+9KkM8MEoxlfjnVGNz6hST8YbIxvv7dvbMuKaSTjFovgz1oPjgqzuuC6LeyIRzwV98b4gV88VefJ+wp7M3oH//hauniv26+o+830PPO2d9eCnQ/8KfoLjPWd71bUxg5cQ6tzts/zP2gY=
自分好みの理詰め問になった。
ルールの量は多いけど、「急カーブ」というテーマで揃えられたので、まぁまぁきれいにまとまったんじゃないだろうか。
さて、5日目の続きで、交差ありループを考えよう。
ボツにしたルールに追加ルールを加えて唯一解にさせる。
ボツにしたルール1
・すべてのマスを通る交差可能ループをひとつつくる
・どの部屋にも右折するマスと左折するマスがある
このルールでは解はふたつである。

片方の盤面のみに当てはまる特徴を抽出できれば、唯一解のルール完成である。
ところがこのふたつの盤面、ほぼ90度回転させただけなのである。
したがって、このふたつの盤面を区別するようなルールとなると、ループの形状のわずかな違いだけで別解をつぶすか、縦方向と横方向でルールを変えるか、部屋に関するルールを見つけるか、太線に関するルールを見つけるかである。可能性が限られている。
縦方向と横方向でルールを変えるのは自分の流儀ではない。他の道を考えよう。
唯一解にするだけなら選択肢は多い。「ひとつの部屋を連続して通るマス数の最大値は5」だの「太線を連続してまたげる最大値は3」だの「長さ2以上で同じ長さの直線部分が連続してはいけない」だの「同じ長さの直線部分が3つ以上連続してはいけない」だの……。
なにが一番自然なルールだろうか……?
うーん……
・すべてのマスを通る交差可能なループをひとつつくる
・どの部屋にも右折するマスと左折するマスがある
・同じ長さの直線が交差してはいけない
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jY+7TgQxDEX7fEZqF7aTETtpeVSIgodWKIoQBR8AiCbR/vvcWB6YEnlzdHT3rjf5/vx5//qgZQ4Tk2ASs508P6HOGNNCjRIpKo7EFkZ/LKO/ldou1F/+9KkM8MEoxlfjnVGNz6hST8YbIxvv7dvbMuKaSTjFovgz1oPjgqzuuC6LeyIRzwV98b4gV88VefJ+wp7M3oH//hauniv26+o+830PPO2d9eCnQ/8KfoLjPWd71bUxg5cQ6tzts/zP2gY=
ルール自体はシンプルなのだが、ちょっと食い合わせが悪い感じがする。
延長戦チャレンジ8日目につづく・・・
8日目
早速だが、失敗作の紹介から。桂馬とびの太線を引いて四角形のブロックに分割するというテーマ。破綻した。下図のような感じ。よくみたら五角形があった。
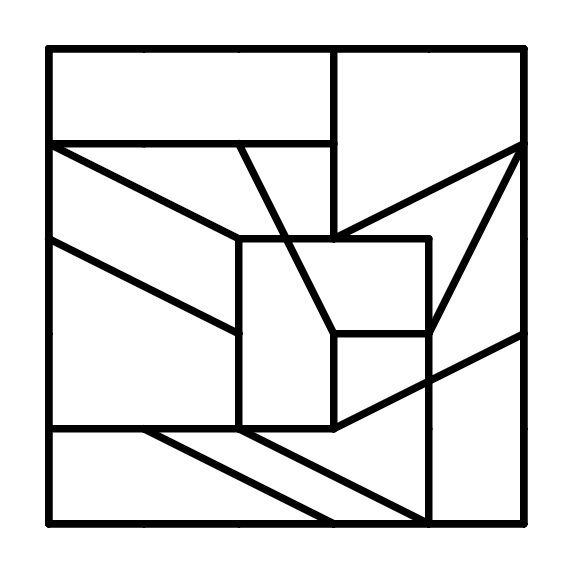
アイデアはよかったと思う。残念だ。
気を取り直して、黒マスパズルでいこう。
3マスブロックが2つあり、黒マスで部屋をふたつに分けるルールと親和性が高い(というか、その意図で作られた盤面である)。
黒マス隣接禁と黒マスひとつながりは、本選で試した。なので、別のルールを考えよう。

黒マスに隣接禁ルールはつけないつもりなので、とりあえず1マス伸ばしてみた。……黒マスがテトロミノなんてちょうどいいんじゃない?
・
・
・
できた。
・盤面にいくつかのテトロミノ(縦横に4つつながった黒マス)を配置する
・黒マスが盤面を分断してはいけない
・どの部屋も黒マスによってふたつの部分に分断される
ぱずぷれで解く
おてごろな理詰めでいいと思う。しかしテトロミノを配置となると、5×5だとやっぱり狭い。
次は数字埋めに挑戦してみる。この挑戦は失敗する可能性が非常に高い。
表出数字がひとつもないので、普通のラテン方陣ルールだと数字の入れ替えによる別解が出る。別解を防ぐには、ルールのどこかで数字に非対称性を持たせる必要がある。
意図的に数字に非対称を持たせて作ったのが、本選投稿作No.12。初めて見たルールだという方も多いでしょうが、ルールでっち上げ界ではわりと定番のルールです。
また、外周ヒントもないので、ラテン方陣系パズルの定番であるABCプレースやビルディングパズルにすることも難しい。
(特に、ABCプレースの場合は、数字の非対称性をつける意味でも難しい)
部屋割りの面積がそろっていないので、各部屋に1~Nが入るルールもやりづらい。
ナナメ隣接可のにょろにょろナンバーとして唯一解(投稿作No.11)だったのは幸運だった。ナナメ隣接可のにょろにょろナンバーとして投稿しましたが、稲葉のパズル研究室の「メイクスネイク」も同じルールです。
思いつくルールをひたすら試していく。
・
・
・
(各列に1~4を入れて、各部屋に空きマスがひとつ・・・)
・
・
・
(各部屋に空きマスがひとつと、1~Nがふたつずつ・・・)
・
・
・
(太線がひとつ違い・・・太線で不連続・・・)
・
・
・
できた。
・すべてのマスに1~3のいずれかの数字が入る
・数字はちょうどその数だけ、縦横一直線につながる(つまり、1×Nの長方形ブロックのフィルオミノ)
・太線で囲まれた部屋内で、1種類の数字が過半数を占めてはいけない
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jY+7TgQxDEX7fEZqF7aTETtpeVSIgodWKIoQBR8AiCbR/vvcWB6YEnlzdHT3rjf5/vx5//qgZQ4Tk2ASs508P6HOGNNCjRIpKo7EFkZ/LKO/ldou1F/+9KkM8MEoxlfjnVGNz6hST8YbIxvv7dvbMuKaSTjFovgz1oPjgqzuuC6LeyIRzwV98b4gV88VefJ+wp7M3oH//hauniv26+o+830PPO2d9eCnQ/8KfoLjPWd71bUxg5cQ6tzts/zP2gY=
……いや、数字埋めじゃないなこれは。やはり数字埋めパズルを作るのは難しかった。
じゃあ次は、バトルシップでいってみる。
5×5マスで、列のヒント数字がなし。各ブロックに2マスの艦影、サイズ3までの標準セットくらいがちょうどいいだろう。解を全列挙できる程度の制約。
ここから追加ルールを入れて唯一解にしよう。
・
・
・
できた。
特殊ルール追加のバトルシップ。使う艦は巡洋艦×1、駆逐艦×2、潜水艦×3の、ミニ標準セット。各部屋に2マスずつ艦影が入る。
艦が入るマスすべてを胴体にもつSnakeを盤面に入れる。Snakeの頭は巡洋艦のマスになり、尾は潜水艦のマスになる。Snakeの頭から尾まで進んだときに、同じサイズの艦が連続していてはいけない。
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jZC/TvUwDMX3PkZmD7GdNLld+TMhBv4IoapCDAxI8PUDxECr+xw8EC92j9MULoIBRT36yfE5tfPy9Hr7fEeZImkmT4yjQUgkk6ZkX9N7XHjSoekdO3KCj93QzNNZN083XT9sabr8wvNuhp52s4vJdb37eIeLybVugGyWEkLWUualpGsJbi4Z15bR4raOYNNxIQ/f//HhbXy8/zc6EkvO3xsX+qUx+/3G2vazEf8/LlNI0QssR5MWPSzqi56U2yNMyqrEGlwneB8N4Fg5grGGsVi9srbEAVMbhwzG2xTeELd4FOMWqyRdOCE/18yQ9rzgWL0R3rR6sd9nDjhJzbHMla2+9pgXjyNY6KqsdVA0QLdN0wvmrQfT/oWGHQ==
・・・めっちゃくちゃなルールですね。でも元ネタがあります。forsmartsのBattleSnake。自分が出会ったパズルの中でも、最も理不尽なルールで最も理不尽な難易度のもののひとつです。
延長戦チャレンジ9日目につづく・・・
9日目
数字埋めの可能性を考えたい。「かずのりのへや」風のルールはどうだろう。
いま試そうとしているルール
・各部屋に空きマスが1つと、1~Nがふたつずつ入る
+なにか都合のよい追加ルール
・
・
・
……なかなかうまくいかないな。
稲葉のパズル研究室の「ナンバースペース」なんてどうだろう。
ナンバースペースのルール
1:縦横の全ての列に指定された範囲の数字(例では1~2)を配置する。
2:どの列も1種類の数字だけ2つ入っているようにする。他は1つずつ入る。
3:各列で2つ入る数字は、その数字とちょうど同じだけ離れていなければならない。
・
・
・
むぅ……
・
・
・
色々試して……
・
・
・
数字のセットを変えてみて……
・
・
・
できた。
・すべての部屋に2,3,4をひとつずつ入れる
・数字のマスから上下左右にその数だけ離れた最大4マスには、他の数字が入らない
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jZC/TvUwDMX3PkZmD7GdNLld+TMhBv4IoapCDAxI8PUDxECr+xw8EC92j9MULoIBRT36yfE5tfPy9Hr7fEeZImkmT4yjQUgkk6ZkX9N7XHjSoekdO3KCj93QzNNZN083XT9sabr8wvNuhp52s4vJdb37eIeLybVugGyWEkLWUualpGsJbi4Z15bR4raOYNNxIQ/f//HhbXy8/zc6EkvO3xsX+qUx+/3G2vazEf8/LlNI0QssR5MWPSzqi56U2yNMyqrEGlwneB8N4Fg5grGGsVi9srbEAVMbhwzG2xTeELd4FOMWqyRdOCE/18yQ9rzgWL0R3rR6sd9nDjhJzbHMla2+9pgXjyNY6KqsdVA0QLdN0wvmrQfT/oWGHQ==
『2,3,4』というのが、恣意的な印象がある(事実、恣意的に決めたのだ)。
こういうときは、似たようなルールで『1,2,3』のバージョンも作ると、恣意的な印象が薄れる。
いま試そうとしているルール
・すべての部屋に1,2,3をひとつずつ入れる
・数字のマスから上下左右にその数だけ離れた最大4マスは、【~ほにゃらら~】という性質をもつ
ほにゃららの候補
・同じ数字が入らない
・ひとつ数字が入る
・ナナメにも何か制約を入れたりする?
・ひとつながりとか入れる?
・各列の制約を入れてみる?
うまくいかない。困ったときは、すべての解を書き出すに限る。ひとつの盤面にのみ成立する性質を見出せば、でっち上げ完了である。
・
・
・
できた。
・すべての部屋に1,2,3をひとつずつ入れる
・数字のマスから上下左右にその数だけ離れた最大4マスのうち、ちょうど1マスにだけ数字が入る
・数字が入らないマスが太線をまたいで隣接してはいけない
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jZC/TvUwDMX3PkZmD7GdNLld+TMhBv4IoapCDAxI8PUDxECr+xw8EC92j9MULoIBRT36yfE5tfPy9Hr7fEeZImkmT4yjQUgkk6ZkX9N7XHjSoekdO3KCj93QzNNZN083XT9sabr8wvNuhp52s4vJdb37eIeLybVugGyWEkLWUualpGsJbi4Z15bR4raOYNNxIQ/f//HhbXy8/zc6EkvO3xsX+qUx+/3G2vazEf8/LlNI0QssR5MWPSzqi56U2yNMyqrEGlwneB8N4Fg5grGGsVi9srbEAVMbhwzG2xTeELd4FOMWqyRdOCE/18yQ9rzgWL0R3rR6sd9nDjhJzbHMla2+9pgXjyNY6KqsdVA0QLdN0wvmrQfT/oWGHQ==
必然性の薄いルールだが、理詰めになってくれたから良しとしよう。それにしても今日は検証がキツいルールが多かった。
延長戦チャレンジ10日目につづく・・・
10日目
あと2個でっち上げれば、通算50個。
ちょうど10日目だし、今日2つ作って終わりとさせたい。
※1個数え忘れています
稲葉のパズル研究室の「飛角プレース」で一個つくりたい。
飛角プレースのルール
1:どのブロック内にも「飛」と「角」の駒を一つずつ配置する。
2:「飛」の効き筋に他の「飛」は入らず、「角」の効き筋に他の「角」は入らない。
(途中に駒があると、そこで効き筋は遮られる。)
通常の飛角プレースでは唯一解にならないのは、本選で検証済み。
なにか別のルールにしよう。
・
・
・
必ず別の駒が効き筋に入る?
・
・
・
必ず別の駒が効き筋に入り、別の邪魔駒も入る?
・
・
・
王を入れてみる?
・
・
・
他国の王を攻撃してはいけない?
・
・
・
他国の王を必ず攻撃する?
・
・
・
ダメだ、うまくいかねえ。
気晴らしに、素直なルールに立ち返ろう。
・
・
・
できた。
・すべてのマスに、マルかバツを入れる
・どの部屋でも、マルが過半数を占める
・マルがタテヨコ一直線に3つ以上連続してはいけない
・バツがナナメ一直線に3つ以上連続してはいけない
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jZC/TvUwDMX3PkZmD7GdNLld+TMhBv4IoapCDAxI8PUDxECr+xw8EC92j9MULoIBRT36yfE5tfPy9Hr7fEeZImkmT4yjQUgkk6ZkX9N7XHjSoekdO3KCj93QzNNZN083XT9sabr8wvNuhp52s4vJdb37eIeLybVugGyWEkLWUualpGsJbi4Z15bR4raOYNNxIQ/f//HhbXy8/zc6EkvO3xsX+qUx+/3G2vazEf8/LlNI0QssR5MWPSzqi56U2yNMyqrEGlwneB8N4Fg5grGGsVi9srbEAVMbhwzG2xTeELd4FOMWqyRdOCE/18yQ9rzgWL0R3rR6sd9nDjhJzbHMla2+9pgXjyNY6KqsdVA0QLdN0wvmrQfT/oWGHQ==
こういう、基本的なルールをたくさん組み合わせるタイプのでっち上げは、でっち上げる過程が面白い。少しずつ調整していく感覚は、既成のパズルだとなかなか味わえない。
でっち上げたパズルが面白い問題かどうかはさておき・・・。
さて、最後は、本選でボツにしたルールをもう一度考え直して終わりにしたい。
ボツにしたルール3
・盤面をいくつかの部屋に分割する
・「部屋の面積」=「その部屋に隣接する部屋数」
盤面の総面積が奇数だから成立しないルールなのだが、黒マスなどを導入すればどうにかなるかもしれない。
・
・
・
うーん、うまくいかないかなぁ。
「隣接する部屋数」ではなく「隣接する黒マス」ではどうだろう。
・
・
・
部屋数が自由だとどうにもならない感があるな……3以下……いや、2以下くらいが妥当な制約か……?
・
・
・
めっちゃ仮定が枝分かれするけど、全部つぶれる……
・
・
・
制約の強さヤバヤバ……
・
・
・
(解が存在するかも怪しいけど、これ面積1の部屋を結合して2にできるから、解が存在しても別解あるだろうなぁ……)
・
・
・
別解見つけた。全解列挙モードに移ろう。
・
・
・
列挙完了。ひとつの盤面にのみ成立する性質をみつけて……
・
・
・
できた。
・以下のルールにしたがって、盤面のいくつかのマスを黒く塗り、太線の分割線を追加する
・黒マスはタテヨコに隣接しない
・黒マスと太線で囲まれた領域の面積は1か2になり、その領域と辺で接する黒マスの個数と一致する
・盤面の初期状態の5つの部屋すべてに、面積2の領域がちょうどひとつずつ入る
penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jZC/TvUwDMX3PkZmD7GdNLld+TMhBv4IoapCDAxI8PUDxECr+xw8EC92j9MULoIBRT36yfE5tfPy9Hr7fEeZImkmT4yjQUgkk6ZkX9N7XHjSoekdO3KCj93QzNNZN083XT9sabr8wvNuhp52s4vJdb37eIeLybVugGyWEkLWUualpGsJbi4Z15bR4raOYNNxIQ/f//HhbXy8/zc6EkvO3xsX+qUx+/3G2vazEf8/LlNI0QssR5MWPSzqi56U2yNMyqrEGlwneB8N4Fg5grGGsVi9srbEAVMbhwzG2xTeELd4FOMWqyRdOCE/18yQ9rzgWL0R3rR6sd9nDjhJzbHMla2+9pgXjyNY6KqsdVA0QLdN0wvmrQfT/oWGHQ==
盤面をズタズタに切っていくルールなのに、初期状態の部屋がルール文に残っちゃうのが、なんとも残念。
追記
ひとつルールを日記に書き忘れていました。
・太線を「カベ」、太線に囲まれた領域を「部屋」と呼ぶ。
・各部屋のカベにふたつずつドアを設置して、すべての部屋を一度ずつ巡って一周できるようにする
・ドアのついたカベの隣にはドアを付けられない
・ドアのついたカベの隣の隣のカベにもドアを付けられない
↓ penpa-editorで解く
https://opt-pan.github.io/penpa-edit/?m=solve&p=jY+7TsUwDIb3PEZmD77kiDQrlwkxcNERqirEwAMAYknUdz9/jSs6IjefPrl/3fj78+f964NOKKvEJCjV6qcwnjQz2qglzdkyZcWRvKTRH9vob21eVuovf/rUBvjgFOer886pzmdEqZvzxsnOe39720aeCglbboqfsR4cF2QNx3VZwo1Eoq/IW/QN+cK/LuhLzBHkNfKCzP7t5hp5xXydwrf+Ph9ue2Y6eD3kr+AVjn3OvtW1s4BrSvM2O+r0P1su
稲葉のパズル研究室の「ドア・ループ」の隣接禁を強めたルール。
あっさり唯一解になったため、存在を忘れていました。
あとがき
でっち上げる過程を保存するつもりで書き始めたのですが、読み返してみると、だいぶ省略しちゃってますね。
後半のほうとか、画像ものっけてないし、いつのまにか「できた」とか言ってるし、何をやっているのかわからない。
いろいろルールを試せばでっち上げられる、ルールでっち上げは楽しい、ということだけでも伝わればいいなと思います。おわり。
この記事が気に入ったらサポートをしてみませんか?
