円周角と中心角

2022年5月18日 20:58

円周角と中心角の関係の意味

円を中心で切り分けるとおうぎ形ができる。

円周のうち、おうぎ形に属する部分（青色の実線で書かれている、点Aから点Bまでの部分の円周）をおうぎ形の弧という。弧の端点A,Bを用いて、$${\overgroup{AB}}$$と書き、弧ABと読む。

ただし、端点A,Bを持つおうぎ形および弧は二通りある。すなわち、実線で囲まれた赤色のおうぎ形以外にも、点線によって囲まれた灰色のおうぎ形が考えられる。長い方（点線）の弧を優弧、短い方（実線）の弧を劣弧と呼んで区別する。単に弧ABといった場合、普通は劣弧を指す。

おうぎ形が円の中心に作る∠AOBをおうぎ形の中心角という。等しい弧を持つおうぎ形はすべて合同であるから、弧が等しければ中心角も等しい。よって、中心角は弧に対して一意に決まるので、弧ABに対する中心角ということもある。

劣弧に対する中心角は赤色の実線で示した角を指し、優弧に対する中心角は灰色の点線で示した角を指す。どちらも半直線OA,OBによって生じる角であるが、前者を劣角、後者を優角と呼んで区別する。通常、半直線OA,OBのなす角というと、劣角を指す。

ある円からおうぎ形を切り取る場合、中心角は弧によって一意に決まると前述した。これにより、角の大きさと弧の長さをうまく対応付けることができるので、角の大きさを弧の長さを用いて表すことができる。

これを一般化して、異なる半径の円も含めて相似なおうぎ形をまとめて扱うならば、結局、角の大きさは、半径に対する弧の長さの比を用いて表せる。

さて、ここからは円と三角形の関係でも調べてみようか。△ABCとその外接円Oを考える。

外接円の円周は、三角形の頂点A,B,Cによって、３つの弧AB,BC,CAに分けられ、それぞれの弧に対して中心角が決まる。それらの中心角と三角形の角の間には、どのような関係があるだろうか。

ここでは、弧ABに対する中心角と三角形の一つの内角Cに注目して、それらの関係について調べてみることにしよう。

二つの数量の関係を調べるための最も基本的で重要な方法は、実際にデータを集めること、すなわち実験と測定および観測である。

原始的には、いかなる事実も観測によって発見されるものである。あらゆる事実の根拠はわれわれの知覚器官を用いた観測にこそあるのだ。

何はともあれ、計測により次の事実が判明する。

角Cの大きさは弧ABに対する中心角の大きさのちょうど$${\dfrac12}$$である。

この結果は偶然だろうか。それとも点Cの取り方によらず常にそうなるのだろうか。

点A,Bおよび外接円Oを固定し、点Cだけを動かすことを考える。△ABCが円Oを外接円に持つための条件は、点Cが外接円Oの円周上に存在することであるから、点Cは円Oの円周上を動くものとする。

この条件において点Cの取り方を変えて計測してみると、弧ABを除いた円周上に点Cがあるとき、角Cの大きさは弧ABに対する中心角のちょうど$${\dfrac12}$$になることがわかる。

この結果から、次のような予想が立てられる。

点Pを弧ABを除いた円周上の任意の点とする。このとき、∠APBは弧ABの中心角の大きさのちょうど$${\dfrac12}$$になる。

これは、弧ABを除いた円周上の点Pの位置によらず、∠APBが弧ABによって一意に決まるということである。ゆえに、弧ABを除く円周上の任意の点Pを頂点に持つ∠APBを、弧ABに対する円周角という。

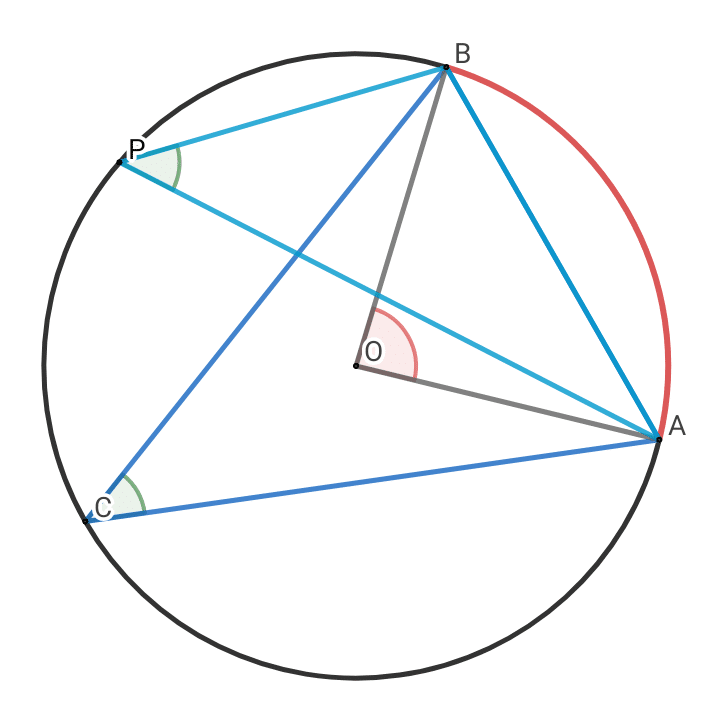
弧ABを除いた円周上の点は無数に存在するから、弧ABに対する円周角もまた無数に存在するが、それらの大きさはすべて等しく、弧ABに対する中心角のちょうど$${\dfrac12}$$である。

$$
\angle APB=\angle ACB=\frac12\angle AOB
$$

円周角は無数に存在するから、それらすべてを計測して、前述した円周角と中心角の関係が成り立つかどうかを確かめることはできない。無数に存在するものをすべて計測するには無限の時間が必要であるのに対し、人が使える時間は有限だからである。

予想が常に成り立つかどうか確認できないということは、それが成り立たない場合がある可能性が排除できないということであり、そのような場合に直面する不安が常につきまとう。これでは安心してその予想を利用することができない。

そこで予想の正しさを確認するために、別のアプローチを用いることにする。すなわち、公理および論理による証明である。

円周角と中心角の関係の証明の発想と方法は、比較的単純かつ簡明である。

今回の予想を立てる際、点Pに課した条件は、点Pが弧ABを除いた円周上にあることだけである。この条件を満たしていれば予想が成り立つことを証明をしたいのだから、証明の出発点は「点Pが弧ABを除いた円周上にあること」となる。

点Pは弧ABを除いた円周上にあるので、点A,B,Pは同一円周上にある。

点A,B,Pが同一円周上にあることから導かれる単純な事実は、円の定義より、どの点も、円の中心Oからの距離が等しくなるということである。

$$
OA=OB=OP
$$

これにより、３つの二等辺三角形ができることがわかる。二等辺三角形の底角が等しいことを利用すれば、円周角と中心角の関係が証明できる。

証明を詳細に書くのはめんどくさいので、証明は割愛する。

円周角と中心角の関係を活用してできることは、普通に考えれば、ある角の半分の大きさの角を別の位置に作図することだろう。しかし、角を半分にすることは角の二等分線で十分に可能なので、それほどありがたみはないかもしれない。

ただ、角の二等分線よりも作図の手順が少ないことと、作図できる角の頂点の位置が異なることを考慮すれば、場面によって使い分けはできそうである。

中心角が180°になるようにすれば、その円周角は90°になる。これにより、容易に直角が作図できる。特に重要なのは、２つの点A,Bが与えられたとき、∠APB=90°となる点Pを見つけられることである。

逆に、円周角が直角になることを利用して、円の直径を求めることもできる。

さて、この数学シリーズもいよいよ終わりが近づいてきた。次が最後の話題となる。締め括りは「三平方の定理」である。

いただいたサポートは書籍購入に使いたいと思います