
格子でつくる60°? 【数学解説#1】
【はじめに】
〈挨拶・前置き〉
こんにちは、ぱぺです。
ブログなのになぜか数学解説を始めました(何で?)
今回は、とあるお話をいたします。
〈解説時に必要な知識〉
まず、今回の解説に必要な数学知識を列挙します。
有理数、無理数 (中3)
三角関数について、公式(数学Ⅱ)
加法定理(数学Ⅱ)
背理法
〈今回の解説対象〉
5月のとある日、ぱぺさんはこう思いました。
「あれ? 格子点どうしをつないだ2線分の成す角って60°にならなくね??」
…こいつどうしてこんな発想に思い立ったんでしょうね。
まあ実際紙に書いたりGeoGebraで試したりしてください。
とにかく、格子点をつなぐだけではきっかり60°を作れないのです。
つまり格子点をつなげて正三角形は作れないんです。
皆さんはこれをどう証明しますか…?
【証明】
2線分の成す角が60°になるような線分の組み合わせが存在すると仮定する。
〈設定〉
2つの線分の一端を揃え、点A(原点)とする。他端はそれぞれB,Cとする。
また、x軸の正部分とABの成す角をp, x軸の正部分とACの成す角をqとする。
点A,B,Cはすべて位置が異なり、π≥p>q>-πである。
B,Cのy座標が負のとき角度p,qも負になり得る。
(C=(1,-1)のときq=-π/4で表し、C=(-1,1)のときq=3π/4と表す。)
∠BAC=rとし、2π>r>0であるとする。また、r=p-qである。
(I) 点B,点Cがどちらもy軸上にないとき


AB,ACは格子点同士を結んだものであるから、tan(p),tan(q)∈ℚ(有理数)…①
よって、加法定理より
tan(r)=tan(p-q)
={tan(p)-tan(q)}/{1+tan(p)tan(q)}
tan(p)-tan(q), 1+tan(p)tan(q)∈ℚ であるから tan(r)∈ℝ…②
しかしr=π/3(=60°)であるから、tan(r)=√3で無理数…③。
よって②と③で矛盾するから、この条件を満たす組み合わせは存在しない。
(II) 点Bがy軸の正部分にあるとき

ACは格子点同士を結んだものであるから、tan(q)∈ℚ(有理数)…①
p=90°だから、加法定理より
tan(r)=tan(p-q)
=tan(90°-q)=1/tan(q)
よって、①よりtan(r)∈ℝ…②
しかしr=π/3(=60°)であるから、tan(r)=√3で無理数…③。
よって②と③で矛盾するから、この条件を満たす組み合わせは存在しない。
(III)点Bがy軸の負部分にあるとき
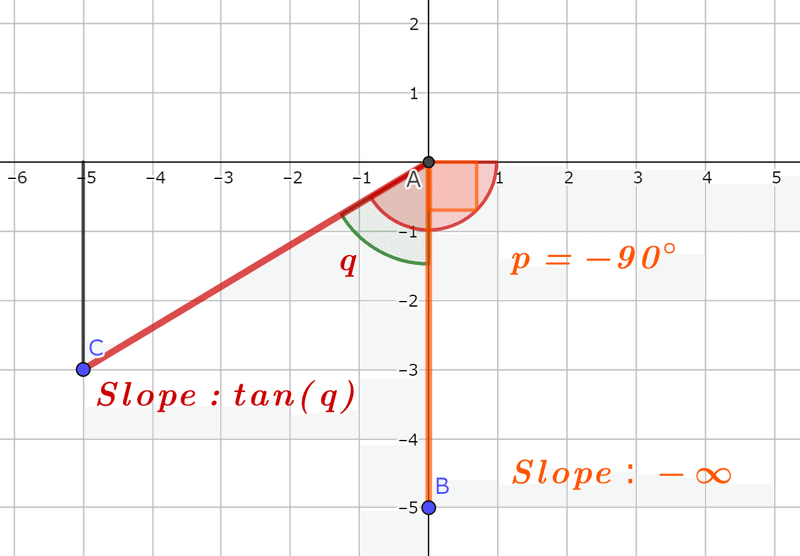
ACは格子点同士を結んだものであるから、tan(q)∈ℚ(有理数)…①
p=-90°だから、加法定理より
tan(r)=tan(p-q)
=tan(-90°-q)
=1/tan(q)
よって、①よりtan(r)∈ℝ…②
しかしr=π/3(=60°)であるから、tan(r)=√3で無理数…③。
よって②と③で矛盾するから、この条件を満たす組み合わせは存在しない。
(IV)点Cがy軸上の正部分にあるとき

ABは格子点同士を結んだものであるから、tan(p)∈ℚ(有理数)…①
q=90°だから、加法定理より
tan(r)=tan(p-q)
=tan(p-90°)
=-1/tan(p)
よって、①よりtan(r)∈ℝ…②
しかしr=π/3(=60°)であるから、tan(r)=√3で無理数…③。
よって②と③で矛盾するから、この条件を満たす組み合わせは存在しない。
(V)点Cがy軸上の負部分にあるとき

ABは格子点同士を結んだものであるから、tan(p)∈ℚ(有理数)…①
q=-90°だから、加法定理より
tan(r)=tan(p-q)
=tan(p+90°)
=1/tan(p)
よって、①よりtan(r)∈ℝ…②
しかしr=π/3(=60°)であるから、tan(r)=√3で無理数…③。
よって②と③で矛盾するから、この条件を満たす組み合わせは存在しない。
(VI)点Bがy軸正部分に、点Cはy軸負部分に存在するとき

p=90°,q=-90°だから、r=p-q=180°
しかし、r=60°であるから、この条件を満たす組み合わせは存在しない。
〈結論〉
(I)~(VI)すべての場合においてこの2線分の組み合わせが存在しないので、
格子点どうしをつないだ2線分の成す角は60°に必ずならない。
【おわりに】
どうでしたか? なんか証明が長ったらしいですね。
初めてこの問題でこんなに長い証明を書きました。分岐がとてつもなく多くてとにかく面倒臭かったですw
でも、しっかりと証明できてよかったと思っています。
【次回予告】
次回の数学解説#2は、
「黄金数…贅沢な名だねぇ。」
黄金数の特徴についてをいくつか解説します。
また次回もお楽しみに~!
【参考文献】
新学習指導要領における算数・数学内容系統一覧表 -啓林館
https://www.shinko-keirin.co.jp/keirinkan/topics/2011/data/math_keitouhyo.pdf
この記事が気に入ったらサポートをしてみませんか?
