線型写像としての行列の固有値とスペクトル【抽象vec sp.のspectrum theoryの具体例として】

最近、少し奮発してC*-algebra(C*環)についての本を買った。

C*-Algebra and operator theoryの1.2節の具体例を取り出して理解を確認したい。とは云え、C＊環の話まではいっておらず、スペクトル理論 spectral theoryの復習のところだ。

導入

1.2.3. Example

Let A be the algebra of upper triangular n×n-matrices. If a∈A, it is elementary that σ(A)={λ_11, λ_22, …, λ_nn}
Similarly, if A=M_n(C) and a∈A, then σ(a) is the set of eigenvalues of a.

Fig 1. one example of upper triangular n×n-matrices.

Thus, one thinks of the spectrum as simultaneously a generalisation of the range of a function and the set of eigenvalues of a finite square matrix.

上で言っていることはつまり、(有限次元の)三角行列のspectrum(の要素)はその行列の対角成分に現れている、ということだ。

スペクトルとレゾルベント

ここで、スペクトル spectrumとレゾルベント resolventの定義から復習しておこう。定義は、宮寺氏の関数解析を参考とした。

出典：宮寺功 関数解析 ちくま文芸文庫

複素数を同値類で切っていったときにスペクトル(内、点スペクトル・連続スペクトル・剰余スペクトル)とレゾルベントとに分けることができ、物理的に重要になるのは点スペクトルである。従って、これには固有値という名前をつけよう、ということだろう。
つまり、
C = σ(T)+ρ(T) = σ_p(T) ⊍ σ_c(T) ⊍ σ_r(T) ⊍ ρ(T)
である。

Murphyの本では、spectrumは次のように定義されている。
それは、algebra Aに対して、その元aが可逆 invertibleであるものを集めた集合をInv(A)として

Fig 2. Definition of Inv(A)

次のように定義されている。

Fig 3. Definition of spectrum σ_A(a)

特に断りが無いので、図3中の1とは、このalgebraの単元のことであろう。
つまり、本テキストでのスペクトルとは点スペクトルのことを指しているものと考えられる。

固有値問題

【環 (U, +, · )】

先ず、n×nの上三角行列 upper triangular n×n-matrixの集合Uに加法と乗法を入れる。このoperationを通常の行列に対するそれであるとすれば、環となる。
このとき、乗法における単元とは単位行列のことであるので、I(アイ)と記す。同様に加法の単元とは、zero行列のことなのでO(オー)と記す。

学部1年生で習う線型数学の知識を用いれば、容易に確認することができる。
更に、正則行列であれば、この可逆元を集めてできる集合U^×は群を成す。これを乗法群と云うのだった。

従って、上のようにしてUについてalgebraをつくることができる。

Case I.　spectrum〈正方行列の場合〉

このUの中で、λI-uが可逆元でないようなuを考える。
これは何かと云えば、以下の固有値問題そのものである。
(あるvector ψ∈(n×1の列vector)に作用するとして、)　uψ=λψ　なる固有値方程式は、右辺が、λψ = λ·Iψとなることに注意して、(u-λI)ψ = 0 と書ける。
ここで、u-λIが正則ならばeigen vector ψ = 0となってしまい矛盾する。従って、u-λIが正則でない i.e. invertibleでないようなu∈Uを集めたいのである。

このようにして得られるλとは、結局固有値問題で得られるeigenvalueのことである。

以下、具体的に3×3の正方行列に対して固有値とその(点)スペクトルを求めてみる。

Fig 4. 考える正方行列

上のsquare matrixの固有値問題を考える。即ち、3-dimのcomplex column vector ψと複素数λに対して、uψ=λψ　を解いてeigen vector ψ_λとeigen value λを求める。

先の議論より、u-λIが正則でなければよいので、線型代数の結果よりdet(u-λI) = |u-λI| = 0を解くと、(1-λ)(λ^2-1)=0 ⇔ λ=-1, 1(重解)となる。
従って、spectrum σ(u) = {-1,1}となる。

ψ = (a, b, c)と置くと、λ=-1のeigen vectorは例えば(1,-1,0)と得られる。
重解のあるλ=1のeigen vectorとして(1,1,0)(0,0,1)等が採れる。

なお、このsquare matrix uの複素転置をとっても同じsquare matrix i.e. u = u†よりHermite matrixなので、eigen vectorを用いて対角化を行うことができる。その方法は、normalized eigen vectorを並べてunitary matrix Uを作ればよかった。

従って、unitary matrixとして以下が考え得る。

Fig 5. unitary matrixの例

実際、

Fig 6. 対角化実行の様子

図6のようにして、対角化を行うことができ、対角線上には固有値が並んでいる。ただ乱雑に並んでいるわけではなく、unitary matrixをつくるときに
U = (ψ_-1, ψ_1, ψ_1)の順に並べていたので、そのlabelに対応する順にeigen valueが対角成分に並んでいる。

このように、有限次元の場合には、線型代数学で学んだ固有値問題の単なる焼き直しのように感じるが、それでは何のためにspectrumという概念を導入したのか分からなくなってしまう。

先の宮寺氏の定義から明らかなように、spectrumは行列と準同型な写像一般の議論に耐えうる(というか、それを想定しての)モノになっている。つまり、spectrum theoryを用いることで、我々は有限次元に拘らず、いわば無限次元の行列の固有値問題に挑もうとしているのである。

Case II.　spectrum〈三角行列の場合〉

簡単のために、3次元で考えよう。

Fig 7. one example of triangular 3×3-matricies

この行列の固有値は、λ=0(重解), 1である。
λ=1に属する固有ベクトルは、例えばψ_1 = (0,0,1)と求まる。
λ=0に属する固有ベクトルは、例えばΨ_0 = (1,0,0)と求まる。

従って、spectrumは{0,1}である。たしかに、対角成分に固有値が並んでいるが、如何せん0が多すぎて感動が薄い。もう一個、少しnon zeroな数を増やして考えてみよう。

Fig 8. one example of triangular 3×3-matricies

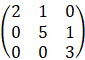
この行列の固有値は、(2-λ)(5-λ)(3-λ) = 0の固有値方程式を解けばよく
λ=2, 3, 5であり、従ってspectrumは{2, 3, 5}である。たしかに対角成分になっている。

と、大仰に書いてはいるが別に難しい話ではなく、detを計算するときに採る小行列において、(1,1)-成分を抜き出したとき以外は必ず小行列内にzero column vectorが含まれてしまうので、固有値方程式には対角成分のtermしか効かないと云うことが分かる。